
- •1). Простые ставки ссудных процентов
- •2). Математическое дисконтирование
- •1) Удержание простых процентов. Банковский учёт векселей
- •1) Темп инфляции. Индекс инфляции
- •2) Ставка, учитывающая инфляцию, для случая простых процентов
- •3) Ставка, учитывающая инфляцию, для случая сложнвх процентов
- •1) Основные понятия
- •2) Нахождение наращенной суммы для простой ренты постнумерандо
- •3) Нахождение наращенной суммы для простой ренты пренумерандо
- •1) Нахождение современной стоимости простой ренты
- •2) Определение величины отдельного платежа простой ренты
- •6). Бессрочная рента пренумерандо
- •2). Погашение займа одним платежом
- •3). Погашение основного долга одним платежом в конце
- •4). Погашение основного долга равными годовыми выплатами
- •5). Погашение займа равными годовыми выплатами
- •5). Погашение займа равными выплатами несколько раз в году
) Основные понятия финансовой математики
Проценты – доход от предоставления капитала в долг.
Обозначение
-
![]() .
.
Процентная ставка – величина, которая характеризует интенсивность начисления процентов.
Первоначальная сумма – исходная, инвестированная сумма.
Обозначение
-
![]() .
.
Наращенная
сумма
![]() –
первоначальная
сумма в совокупности с начисленными
процентами.
–
первоначальная
сумма в совокупности с начисленными
процентами.
Понятно,
что
![]() .
.
Коэффициент
наращения
![]() –
показывает,
во сколько раз возросла первоначальная
сумма, т.е.
–
показывает,
во сколько раз возросла первоначальная
сумма, т.е.
![]() .
.
Период начисления – промежуток времени (весь), за который начисляются проценты.
Интервал начисления – минимальный промежуток времени, по прошествии которого начисляются проценты.
_________________________
Пример. Первоначальная сумма может быть инвестирована на два года (период начисления), а проценты будут начисляться каждый месяц (интервал начисления).
_________________________
Существуют два способа начисления процентов.
Декурсивный способ – проценты начисляются в конце каждого интервала начисления.
Декурсивная процентная ставка называется ссудным процентом.
Антисипативный (предварительный) способ – проценты начисляются в начале каждого интервала начисления.
Антисипативная процентная ставка называется учётной ставкой.
Сами проценты бывают двух видов: простые и сложные.
Простые проценты – проценты, которые применяются к первоначальной сумме в течение всего периода начисления.
Сложные проценты – проценты, которые применяются к текущей наращенной сумме в каждом интервале начисления.
Лекция 2. Простые ставки ссудных процентов
1). Простые ставки ссудных процентов
Пусть:
- первоначальная сумма;
- наращенная сумма;
![]() - процентная ставка за интервал
- процентная ставка за интервал
![]() начисления, проценты - простые.
начисления, проценты - простые.
Пусть
прошёл интервал начисления
,
тогда наращенная сумма за этот промежуток
времени
![]() равна
равна
![]() .
.
Пусть прошёл ёще один интервал времени , т.е.
![]() .
.
Аналогично
вычисляется наращенная сумма
за весь период начисления
![]()
![]()
или окончательно
![]() .
(1)
.
(1)
_________________________
Пример.
Первоначальная сумма, равная
![]() рублей, помещена в банк на
рублей, помещена в банк на
![]() года под
года под
![]() годовых (проценты – простые). Найти
наращенную сумму.
годовых (проценты – простые). Найти
наращенную сумму.
Решение. По формуле (1) находим
![]() ,
,
где проценты нужно выразить в виде десятичной дроби (!), ибо в виде десятичной дроби происходят вычисления,
![]() .
.
Поэтому
![]() (рублей).
(рублей).
_________________________
На
формулу (1) можно смотреть как на связь
между четырьмя параметрами
![]() :
если неизвестен один из этих параметров,
то его можно найти через остальные.
:
если неизвестен один из этих параметров,
то его можно найти через остальные.
а)
Найти период начисления
![]() (в годах), если известны:
,
первоначальная сумма;
,
наращенная сумма;
-
процентная ставка за год (проценты -
простые)
(в годах), если известны:
,
первоначальная сумма;
,
наращенная сумма;
-
процентная ставка за год (проценты -
простые)
Из формулы (1) найдём
![]() .
.
Поэтому период начисления равен
![]() .
(2)
.
(2)
_________________________
Пример.
Первоначальная сумма, равная
![]() рублей, помещена в банк под
рублей, помещена в банк под
![]() годовых (проценты – простые). Наращенная
сумма оказалась равной
годовых (проценты – простые). Наращенная
сумма оказалась равной
![]() рублей. Найти период начисления.
рублей. Найти период начисления.
Решение. Выразим в виде десятичной дроби указанные проценты
![]() .
.
Поэтому по только что найденной формуле
![]() (года).
(года).
б) Найти простую процентную ставку , зная первоначальную сумму , наращенную сумму и период начисления (в годах)
Из недавно полученной формулы (2), умножая левую и правую части этого равенства на и деля на , получим
![]() .
.
_________________________
Пример.
Первоначальная сумма, равная
![]() рублей, была помещена в банк. Наращенная
сумма оказалась равной
рублей, была помещена в банк. Наращенная
сумма оказалась равной
![]() рублей, период начисления был - полгода.
Найти простую процентную ставку.
рублей, период начисления был - полгода.
Найти простую процентную ставку.
Решение.
Понятно,
что
![]() ,
,
![]() ,
,
![]() .
Поэтому из только что найденной формулы
получим
.
Поэтому из только что найденной формулы
получим
![]()
или в процентах
![]() (годовых).
(годовых).
Сложные ставки ссудных процентов
Пусть: - первоначальная сумма; - наращенная сумма; - годовая процентная ставка ссудных процентов, проценты - сложные. Проценты начисляются в конце каждого интервала начисления к величине наращенной суммы, которая была в начале этого интервала начисления.
Итак,
пусть прошёл первый год с момента
открытия вклада. Тогда наращенная сумма
![]() за первый год хранения вклада равна
за первый год хранения вклада равна
![]() .
.
При
прошествии второго года хранения вклада
наращенная сумма
![]() будет иметь вид
будет иметь вид
![]() .
.
Аналогично,
сразу после
-ого
года хранения вклада наращенная сумма
![]() будет иметь вид
будет иметь вид
![]() .
.
Окончательно
![]() .
(4)
.
(4)
_________________________
Пример. Первоначальная сумма, равная рублей, помещена в банк на года под годовых (проценты – сложные). Найти наращенную сумму.
Решение.
По
формуле (4) (в ней
![]() )
)
![]() (рубля).
(рубля).
_________________________
Используя формулу (1), можно находить, зная 3 параметра, любой другой.
а) Найти период начисления (в годах), если известны: , первоначальная сумма; , наращенная сумма; - процентная ставка за год (проценты - сложные)
Из формулы (4) найдём
![]() .
.
Найдём
логарифм по основанию «![]() »
»
![]() .
.
По свойству логарифма
![]() .
.
Поэтому окончательно получим
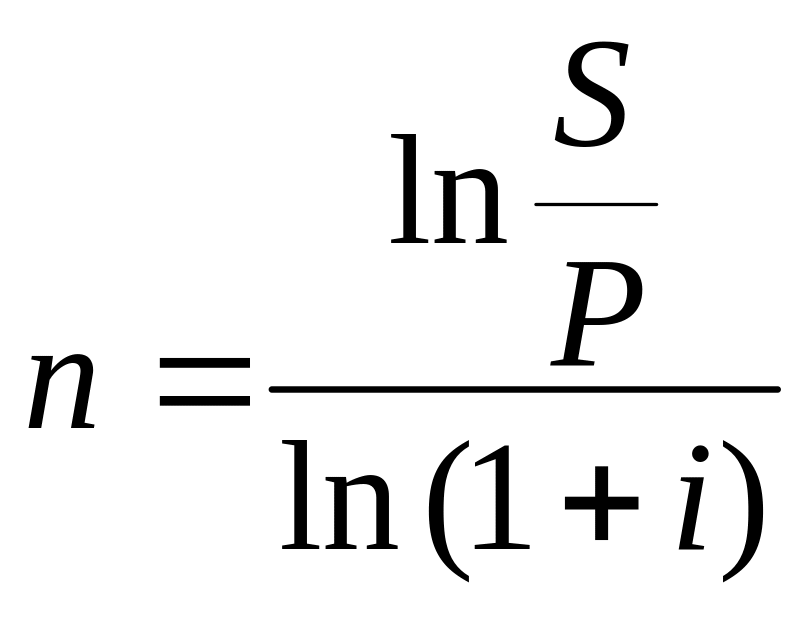 .
.
_________________________
Пример. Первоначальная сумма, равная рублей, помещена в банк под годовых (проценты – сложные). Наращенная сумма оказалась равной рублей. Найти период начисления.
Решение. По только что найденной формуле ( )
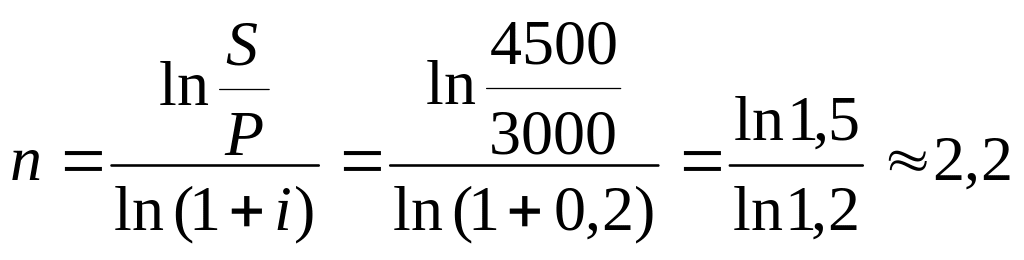 (года).
(года).
б) Найти сложную годовую процентную ставку , зная первоначальную сумму , наращенную сумму и период начисления (в годах)
Из формулы (4) находим
![]() ,
,
откуда сложную годовую процентную ставку имеет вид
![]() .
.
_________________________
Пример.
Первоначальная сумма, равная
рублей, была помещена в банк. Наращенная
сумма оказалась равной
![]() рублей, период начисления был – 3 года.
Найти сложную годовую процентную ставку.
рублей, период начисления был – 3 года.
Найти сложную годовую процентную ставку.
Решение.
Понятно,
что
![]() ,
,
![]() ,
,
![]() .
Поэтому из только что найденной формулы
получим
.
Поэтому из только что найденной формулы
получим
![]() .
.
Иными
словами,
![]() годовых.
годовых.
