Модели выбора решений в условиях определенности в сфере туризма и гостеприимства.
Часть 1. Модели выбора решений в условиях определенности.
В
практической деятельности приходится
рассматривать сложные объекты, которые
невозможно целостно сопоставить. В
таких случаях выделяют существенные
показатели этих объектов, а затем
проводят сравнение их значений. При
этом первичная информация задается в
виде таблицы сравниваемых объектов
,
все наименования показателей
и значения этих показателей по каждому
объекту
.
В таблице 1.1 приведен перечень характеристик
дополнительных услуг санаториев, а
также оценки одного эксперта этих услуг
Таблица 1.1
Санаторий |
Качество дополнительной услуги (мин. 0 баллов, макс. 10 баллов) |
Цена у.е. |
|||||
Бассейн |
Водный массаж |
Тренажерный зал |
Спортзал |
Кинотеатр |
Информационная служба |
||
А |
9 |
0 |
8 |
10 |
4 |
2 |
235 |
Б |
3 |
4 |
5 |
6 |
7 |
8 |
456 |
В |
3 |
4 |
5 |
9 |
7 |
2 |
234 |
Г |
3 |
4 |
6 |
7 |
8 |
9 |
654 |
Д |
6 |
7 |
8 |
9 |
5 |
7 |
478 |
Задача: при помощи интегрального критерия и критерия цена/качество сделать выбор санатория с лучшими дополнительными услугами.
Для
выделения предпочтения необходимо
ввести систему решающих правил. Например,
если по каждому показателю
можно
вычислить его вес
,
определяющий его значимость, то взвешенную
сумму этих показателей можно рассматривать
как суммарную оценку объекта
Тогда
можно ввести решающее правило:
предпочтительнее
,
если
.
Этот способ сравнения называется
сравнением при помощи интегрального
критерия.
Разделим цену на интегральную оценку
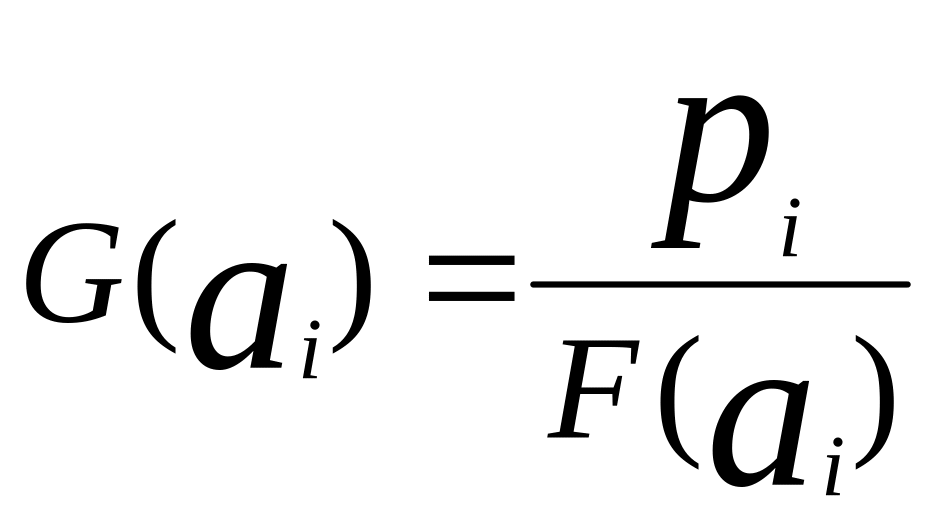
Тогда
можно ввести решающее правило:
предпочтительнее
,
если
.
Этот способ сравнения называется
сравнением при помощи
критерия цена/качество.
По
указанной системе решающих правил
отношение, выражающее доминирование,
определяется построением матрицы
попарного сравнения
,
элемент которой определяется таким
образом
1, если
равнозначен
0,
если
менее значим, чем
2, если предпочтительнее
В таблице 1.1 приведен список дополнительных услуг санаториев. Сопоставим эти услуги с помощью метода парных сравнений, а результат запишем в таблицу 1.2.
Результат парных сравнений показал, что наибольший вес имеет тренажерный зал, а наименьший вес водный массаж и информационная служба. Правильность заполнения таблицы определяется равенством
Таблица 1.2
|
Бассейн |
Водный массаж |
Тренажерный зал |
Спортзал |
Кинотеатр |
Информационная служба |
Сумма |
Вес показателя |
Бассейн |
1 |
2 |
1 |
1 |
0 |
2 |
7 |
0,1944 |
Водный массаж |
0 |
1 |
0 |
0 |
1 |
2 |
4 |
0,1111 |
Тренажерный зал |
1 |
2 |
1 |
1 |
2 |
1 |
8 |
0,2222 |
Спортзал |
1 |
2 |
1 |
1 |
1 |
1 |
7 |
0,1944 |
Кинотеатр |
2 |
1 |
0 |
1 |
1 |
1 |
6 |
0,1667 |
Информационная служба |
0 |
0 |
1 |
1 |
1 |
1 |
4 |
0,1111 |
Затем определяем вес показателей по формуле
Следует отметить, что
Используя таблицу 1.3, в которой приведены оценки качественного содержания показателя, получим интегральные оценки дополнительных услуг в санаториях
Таблица 1.3
Санатории |
Бассейн |
Водный массаж |
Тренажерный зал |
Спортзал |
Кинотеатр |
Информационная служба |
Значение интегрального признака |
А |
9 |
0 |
8 |
10 |
4 |
2 |
6,36111 |
Б |
3 |
4 |
5 |
6 |
7 |
8 |
5,36111 |
В |
3 |
4 |
5 |
9 |
7 |
2 |
5,27778 |
Г |
3 |
4 |
6 |
7 |
8 |
9 |
6,05556 |
Д |
6 |
7 |
8 |
9 |
5 |
7 |
7,08333 |
Максимальная интегральная оценка соответствует санаторию Д, используя значения цен дополнительных услуг, сравним дополнительные услуги по критерию цена/качество.
Таблица 1.4
Санатории |
Цена |
Значение интегрального признака |
Значение критерия цена/качество |
А |
235 |
6,36111 |
36,9432 |
Б |
456 |
5,36111 |
85,057 |
В |
234 |
5,27778 |
44,3368 |
Г |
654 |
6,05556 |
108 |
Д |
478 |
7,08333 |
67,4824 |
Минимальное значение по критерию цена/качество соответствует санаторию А.