
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«Уральский федеральный университет
имени первого Президента России Б.Н. Ельцина»
Кафедра теоретических основ радиотехники
Проверил:
Трухин М.П.
_______________________
Идентификация линейной системы
индивидуальное домашнее задание №3 (вариант 13)
по дисциплине Моделирование систем
Выполнил
студент группы Р-390702
Сальников М.С.
Екатеринбург 2012
Цель работы:
Построить линейную модель, наилучшим образом описывающую некоторую систему, экспериментальная зависимость выхода от входа которой приведена ниже:
Исходные данные:
Исходные данные находятся в файле Zad13.dat.
Zad13
Input Output
-7.578199e-003 -1.413060e-003
4.225042e-002 1.319992e-001
-1.080474e-001 -4.227444e-002
6.773332e-002 -2.290479e-001
-1.606172e-001 1.907608e-001
5.648098e-002 -1.246169e-001
5.360484e-002 -3.121873e-002
1.230679e-001 1.127882e-001
-1.941673e-001 9.730870e-002
1.229011e-001 -2.392887e-001
1.098203e-001 1.375965e-001
-3.062848e-002 -5.221163e-002
4.256433e-002 2.180293e-001
-2.529895e-001 -1.473808e-001
3.001549e-001 1.207871e-001
-1.576491e-001 -4.613972e-002
9.574609e-002 -2.594379e-001
-9.318000e-002 4.681008e-001
-2.074733e-001 -2.862107e-001
4.539094e-001 -2.527674e-001
-1.415972e-001 3.579107e-001
-1.364743e-001 1.643520e-001
1.671388e-001 -3.674189e-001
-8.107914e-002 7.707797e-002
-2.436661e-001 8.604369e-002
1.055630e-001 -3.093571e-001
-7.061382e-003 3.270887e-001
-4.801416e-002 -2.863485e-001
1.367976e-001 2.593665e-001
-1.951072e-001 -9.873933e-002
1.620577e-001 -1.738870e-001
-1.919791e-001 -2.034715e-002
1.661100e-001 1.356380e-001
-2.594936e-001 -2.128608e-001
6.197313e-002 1.997006e-001
-1.069342e-001 -1.844275e-001
2.655563e-001 6.505189e-002
-9.330318e-002 2.893951e-001
3.795010e-004 -3.465948e-001
1.824154e-001 1.118232e-001
-1.841171e-001 1.034810e-001
2.319560e-001 -2.149640e-001
-5.894448e-002 2.934124e-001
-1.509316e-001 1.180696e-001
7.792348e-002 -3.829954e-001
1.603255e-001 8.745378e-002
-4.032769e-001 1.779446e-001
1.534051e-001 -2.959633e-001
3.270342e-001 2.163522e-003
-2.287076e-001 2.127695e-001
-1.521307e-001 -1.512271e-001
9.255596e-002 -4.918692e-002
-6.059457e-002 2.982656e-001
-1.652933e-002 -3.432511e-001
3.564501e-002 7.307208e-002
-5.805845e-002 1.693058e-002
3.995267e-002 1.111679e-001
-8.688788e-002 8.628512e-002
1.191287e-001 -1.718185e-001
-2.941947e-002 -2.165309e-001
1.326147e-001 3.314874e-002
-1.325612e-001 2.282363e-001
-2.669307e-001 7.578578e-002
2.305702e-001 -3.573938e-001
2.010852e-001 1.874605e-001
-3.523083e-001 -5.681270e-002
2.782833e-001 7.835969e-003
-6.426272e-002 6.856926e-002
4.250081e-002 1.443485e-002
-2.550953e-003 2.108797e-001
1.182015e-001 2.431962e-002
3.771232e-002 -8.516950e-002
-1.676269e-002 2.313044e-002
2.963470e-002 -8.181948e-002
4.932032e-002 2.364057e-001
-3.613195e-001 -7.072190e-002
4.290945e-001 -3.558293e-001
-1.172073e-001 4.161413e-001
-3.585259e-001 -1.990548e-001
3.009225e-001 -2.572058e-001
-3.060854e-001 1.972225e-001
-1.334731e-002 -1.977067e-001
2.535555e-001 1.620025e-001
-2.098371e-001 7.420119e-002
9.171854e-002 -3.182188e-001
-4.120212e-003 5.679353e-002
-2.321784e-001 1.357861e-001
2.397664e-001 -3.363484e-002
6.320958e-002 -1.317524e-001
7.255577e-002 6.791649e-002
-2.193270e-001 2.414054e-001
9.765336e-002 -2.798423e-001
1.488638e-002 2.039072e-001
-2.568499e-001 6.736527e-002
6.374248e-002 -2.126124e-001
1.983896e-001 4.035432e-002
-2.101909e-001 2.884510e-001
-4.408622e-002 -2.500404e-001
3.998361e-001 -1.322752e-001
-3.531967e-001 3.802367e-001
-2.730883e-004 -3.123904e-005
3.000942e-003 7.090830e-003
-1.053220e-002 -3.798261e-002
-2.225292e-002 1.403413e-004
6.689171e-004 4.618118e-002
9.149922e-002 4.600774e-002
-1.010477e-002 -7.300081e-003
8.040180e-003 8.898335e-003
-2.461274e-002 -4.856598e-002
-1.274663e-002 -6.341904e-003
-2.390731e-002 1.018495e-002
1.715378e-002 -2.599681e-002
-3.532361e-002 -4.297719e-003
-1.238286e-002 -5.172938e-002
-5.926742e-003 5.862737e-002
5.864770e-003 -6.456161e-002
-3.876240e-002 -1.626810e-003
2.230863e-003 5.748727e-002
7.301867e-002 -2.841223e-002
-3.466645e-002 2.912512e-002
-9.535985e-003 -5.645964e-003
3.427510e-002 -5.082754e-003
-3.039844e-002 -5.909173e-002
-8.249334e-002 -4.388025e-003
6.353569e-002 6.346213e-002
7.378651e-002 4.606333e-002
3.577758e-003 4.765842e-002
6.630503e-002 -2.095882e-002
-5.086441e-002 2.397642e-002
2.819005e-002 -4.217390e-002
-3.093808e-002 1.339691e-002
1.667313e-003 1.568407e-002
7.470997e-002 8.749511e-002
1.502330e-002 -5.257583e-002
-7.857172e-003 8.228092e-002
7.739730e-002 -1.436221e-003
-9.531661e-003 3.268565e-002
-1.739171e-004 -3.812488e-002
-3.448307e-002 -7.385736e-002
-7.104819e-002 1.700286e-002
3.007080e-002 -1.046948e-002
6.742364e-003 -3.745097e-003
-5.355291e-002 -2.178769e-002
1.531246e-002 -1.774186e-002
-2.852082e-002 -4.142814e-002
-3.695999e-002 3.618647e-002
3.886575e-002 1.019259e-002
6.045650e-002 4.979441e-002
2.085131e-003 1.309531e-002
-2.154928e-002 -4.410314e-002
-5.326451e-003 -4.791350e-003
8.536636e-003 4.786541e-002
4.061532e-002 3.390584e-002
2.497132e-002 -4.526538e-002
-6.441225e-002 2.142609e-002
6.527392e-002 3.620866e-002
1.619711e-002 1.169282e-002
-9.084083e-003 -2.970636e-002
-1.918976e-002 -2.495195e-002
-4.375640e-002 -2.181312e-002
2.967809e-002 7.144986e-002
4.896773e-002 1.565100e-002
3.876281e-003 -1.385692e-002
1.555392e-002 1.324088e-002
-2.313411e-002 1.379800e-002
4.065825e-003 -4.673575e-002
1.118735e-002 6.472083e-002
7.624571e-003 -4.070445e-002
-2.760463e-002 -1.812240e-002
-2.513106e-002 -1.802683e-002
-1.360755e-002 -4.885360e-002
-8.522154e-002 -8.499649e-002
-5.962310e-002 -1.812615e-002
1.168814e-002 7.830248e-003
-5.610506e-004 1.567611e-002
-6.494811e-003 -4.873291e-002
1.520708e-002 5.358153e-002
-1.861413e-002 2.496478e-003
4.260538e-002 -1.869857e-002
6.187943e-003 6.840655e-002
2.610916e-002 3.365242e-002
1.009738e-001 7.456618e-002
3.439526e-002 4.537588e-002
-3.712307e-003 -6.338615e-002
-3.461043e-002 -1.661149e-002
-1.996144e-002 3.507166e-002
6.318053e-002 4.950961e-002
6.590212e-002 3.827729e-002
-3.860949e-002 -7.250337e-002
-5.307433e-002 -1.008202e-002
-4.110592e-003 -6.322497e-003
2.204504e-002 -1.101034e-002
-5.092218e-002 4.087493e-003
3.123812e-002 -1.335500e-003
1.263686e-002 1.924932e-002
9.632561e-003 2.881361e-002
2.603784e-003 -1.750401e-002
5.713800e-003 -2.541763e-002
-2.610025e-002 1.515399e-002
-3.135532e-002 -2.828461e-002
Coeff
Pr = 1
0.131148 -0.262295 -0.393443
1.000000 0.688525 0.737705
0.036036 -0.036036 -0.180180 -0.108108
1.000000 -0.927928 0.333333 -0.045045
Ход работы:
Перестановка исходных данных с помощью скрипт-файла:
%reshape script
fin=fopen('Zad13.dat');
t1=fgetl(fin);
t2=fgetl(fin);
a=fscanf(fin,'%e %e',[2 inf]);
a=a';
fclose(fin);
l=size(a,1);
l2=round(l/2);
for i=1:100
In(2*i-1)=a(i,1);
In(2*i)=a(i,2);
Ou(2*i-1)=a(i+100,1);
Ou(2*i)=a(i+100,2);
end
subplot(211);
plot(In),title('Входной процесс');
subplot(212);
plot(Ou,'g'),title('Выходной процесс');
График исходных данных после преобразования представлен на рисунке 1:
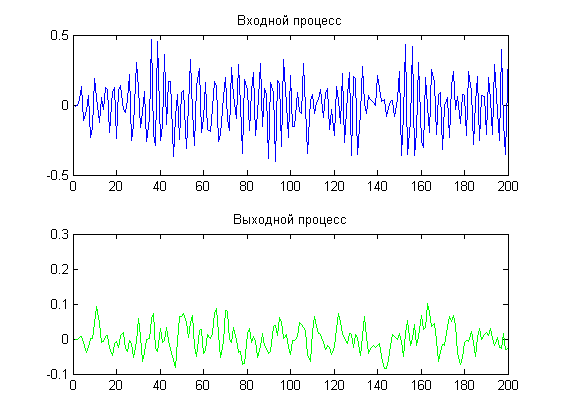
Рисунок 1. Заданные входной и выходной процесс после процедуры перестановки отсчетов.
Идентификация модели по половинному набору данных
После удаления постоянной составляющей и трендов, полученные данные (рисунок 2) мы будем использовать для задач идентификации и верификации.
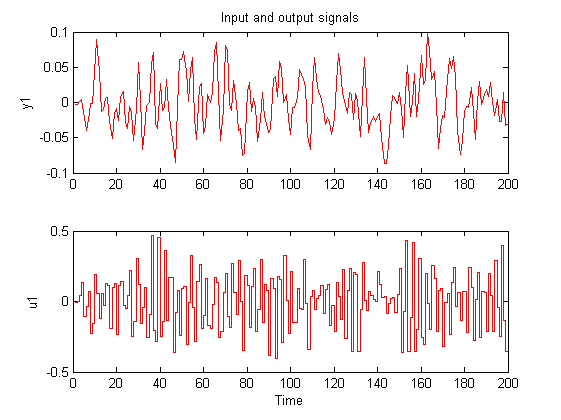
Рисунок 2. Входной и выходной процессы после удаления постоянной составляющей и трендов.
Первая половина данных (рисунок 3):
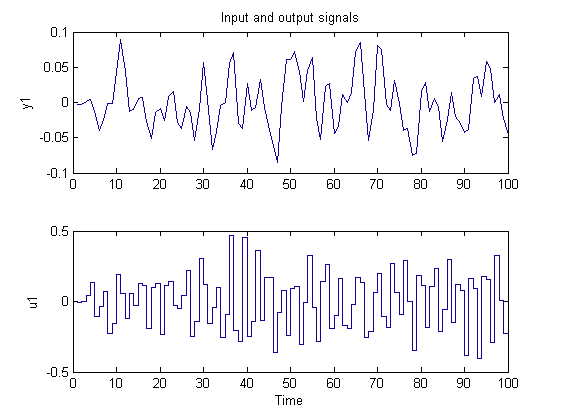
Рисунок 3. Первая половина данных о входном и выходном процессе.
Ее мы будем использовать для проведения процедуры идентификации. Вторую половину данных мы будем использовать для верификации полученной модели. График второй половины представлен на рисунке 4:
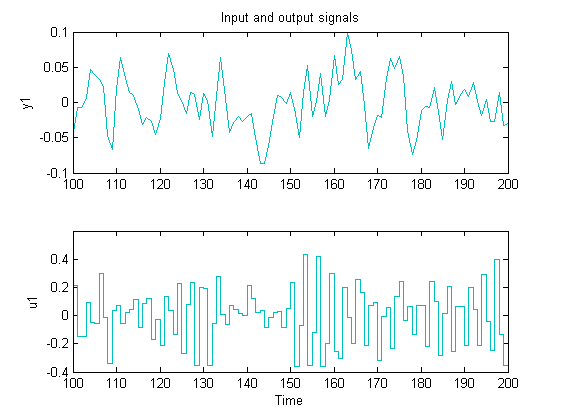
Рисунок 4. Вторая половина данных о входном и выходном процессе.
Графики, полученные в результате выполнения команды Quick Start на вкладке Model Output представлены на рисунке 5:
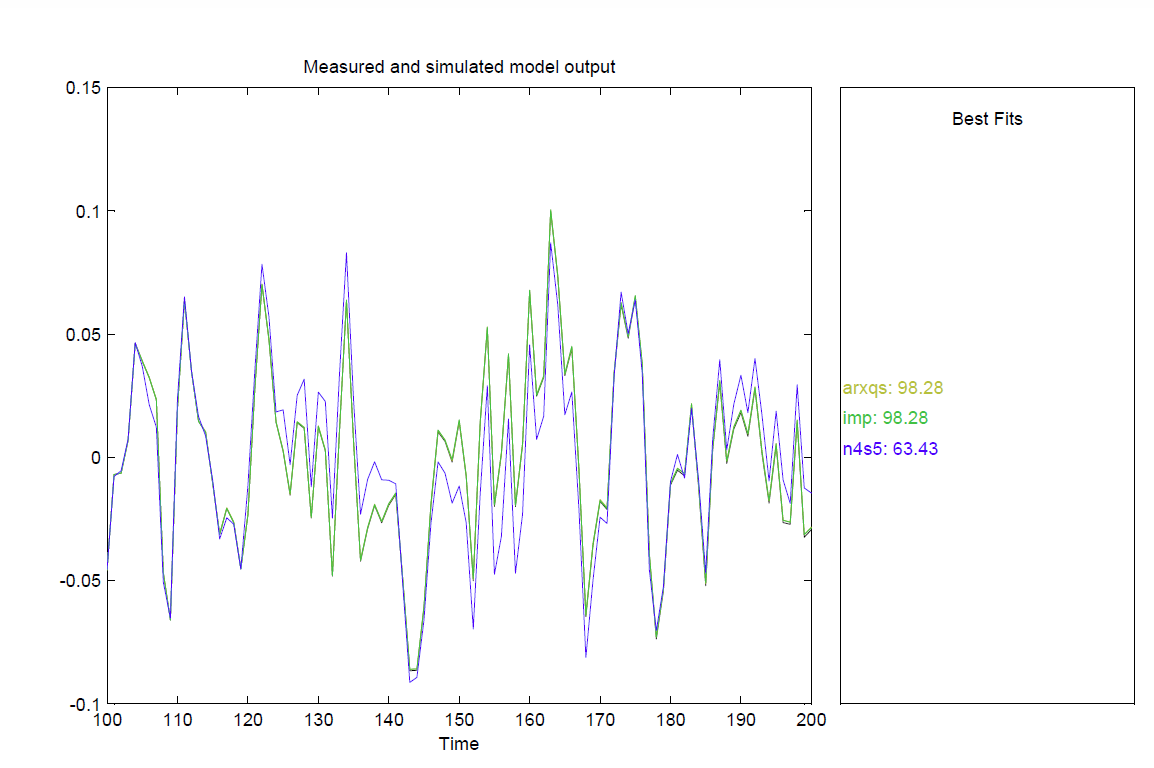
Рисунок 5. Сравнение выходов различных моделей, при заданном входе.
Как мы видим из последнего рисунка, две модели: arxqs и imp моделируют данную систему с точностью в 98,28%. Поэтому выберем любую из них для продолжения. Пусть это будет модель arxqs.
Перенесем сведения об этой модели в командное окно MATLAB:
Discrete-time IDPOLY model: A(q)y(t) = B(q)u(t) + e(t)
A(q) = 1 - 0.9285 (+-0.002718) q^-1 + 0.3343 (+-0.003824) q^
-2 - 0.04562 (+-0.002581) q^-3 + 0.0003007 (+-0.001055) q^-4
B(q) = 0.03601 (+-0.0001095) - 0.03604 (+-0.0001208) q^-1 - 0.1802 (
+-0.0001483) q^-2 - 0.108 (+-0.0005042) q^-3
Estimated using ARX from data set eDat
Loss function 1.40048e-008 and FPE 1.62456e-008
Sampling interval: 1
Выведем список параметров этой модели командой get(arxqs)
a: [1 -0.9285 0.3343 -0.0456 3.0068e-004]
b: [0.0360 -0.0360 -0.1802 -0.1080]
c: 1
d: 1
f: 1
da: [0 0.0027 0.0038 0.0026 0.0011]
db: [1.0946e-004 1.2083e-004 1.4826e-004 5.0420e-004]
dc: 0
dd: 0
df: 0
na: 4
nb: 4
nc: 0
nd: 0
nf: 0
nk: 0
InitialState: 'Auto'
Name: 'arxqs'
Ts: 1
InputName: {'u1'}
InputUnit: {''}
OutputName: {'y1'}
OutputUnit: {''}
TimeUnit: ''
ParameterVector: [8x1 double]
PName: {}
CovarianceMatrix: [8x8 double]
NoiseVariance: 1.5915e-008
InputDelay: 0
Algorithm: [1x1 struct]
EstimationInfo: [1x1 struct]
Notes: [8x30 char]
UserData: []
Определение параметров дискретного фильтра, определяющего модель системы
Теперь выделяем коэффициенты дискретного фильтра, представляющего линейную модель системы.
[a,b]=th2poly(arxqs)
Полученные коэффициенты:
a = 1.0000 -0.9285 0.3343 -0.0456 0.0003
b = 0.0360 -0.0360 -0.1802 -0.1080
Коэффициент а(4) получился всего в три раза больше погрешности его определения. Поэтому его можно опустить. Таким образом, порядок этой модели равен трем (порядок чилсителя 3и порядок знаменателя так же 3).
Пропускаем через этот фильтр вторую половину данных
In2=In(101:200);
Ou2=Ou(101:200);
Ou22=filter(b,a,In2);
plot([Ou22 Ou2]);
Результаты сравнения идентификации с реальными данными приведены на рисунке 6:
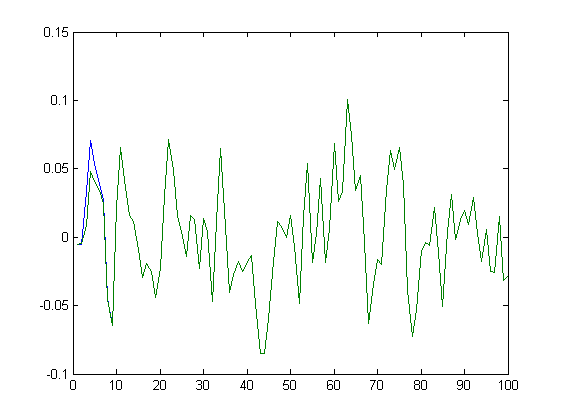
Рисунок 6. Сравнение выхода созданного фильтра и заданного результата.
Как видно из этого рисунка, результат на выходе фильтра практически полностью повторяет заданный выход. Исключение составляют лишь первые 8 отсчетов. Эта разница обусловлена переходным процессом в фильтре. Оценим среднеквадратичную ошибку фильтра с первого отсчета и ошибку после завершения переходного процесса (то есть с 9 отсчета):
Err1=sqrt(sum((Ou22-Ou2).^2)/length(Ou2))
Err1 = 0.0037
Err1=sqrt(sum((Ou22(9:end)-Ou2(9:end)).^2)/length(Ou2(9:end)))
Err1 = 1.6232e-005
Видно, что переходной процесс внес достаточно большую ошибку, однако если его устранить, ошибка получается достаточно малой.
Идентификация модели по полному набору данных
Проведем все то же самое для полного набора данных. На этот раз все 200 отсчетов будут играть свою роль как в идентификации модели, так и в ее верификации.
На этот раз, модель imp получила небольшое превосходство над моделью arxqs. (Напомним, в прошлый раз они были одинаково точны) График сравнения этих моделей представлен на рисунке 7:
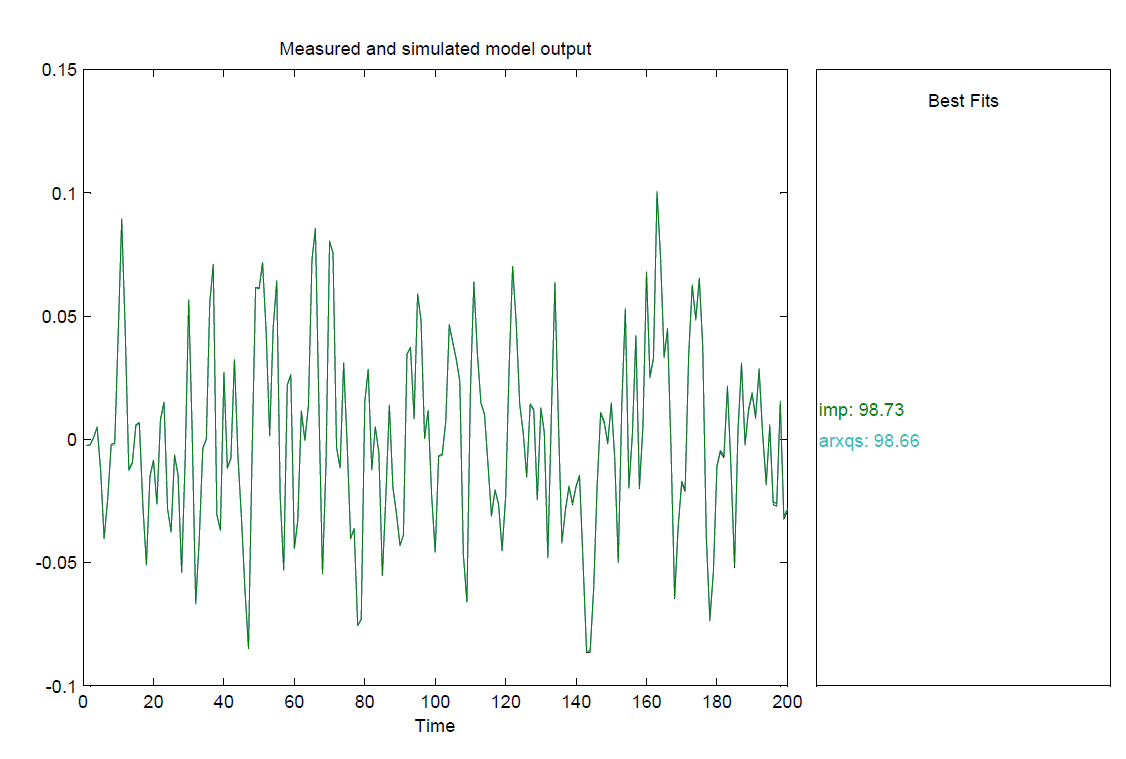
Рисунок 7. Сравнение моделей imp и arxqs на полном наборе данных
Перенесем сведения об этой модели в командное окно MATLAB:
Multivariable ARX model
A0*y(t)+A1*y(t-T)+ ... + An*y(t-nT) =
B0*u(t)+B1*u(t-T)+ ... +Bm*u(t-mT) + e(t)
A0: 1
B0: 4.4972e-004
B1: 3.5577e-004
B2: 2.3366e-004
B3: 2.8886e-004
B4: 3.9300e-004
B5: 0.0362
B6: -0.0021
B7: -0.1943
B8: -0.2858
B9: -0.2005
B10: -0.0992
B11: -0.0384
B12: -0.0111
B13: -0.0023
B14: 4.5327e-004
B15: 3.0531e-004
B16: 3.1413e-004
B17: 9.8794e-006
B18: 3.2476e-004
B19: 7.0819e-005
B20: 2.8166e-004
B21: 2.7022e-004
B22: 2.0300e-004
B23: 1.5447e-004
B24: 4.7703e-004
B25: 4.9264e-004
B26: 6.4706e-004
B27: 5.3537e-004
B28: 5.7501e-004
B29: 3.8070e-004
B30: 2.5713e-004
B31: 2.3637e-004
B32: 3.7335e-004
B33: 2.8123e-004
B34: 5.8682e-004
B35: 5.1762e-004
B36: 4.9276e-004
B37: 4.3039e-004
B38: 4.6553e-004
B39: 3.9972e-005
B40: 6.0557e-005
B41: -2.5077e-004
B42: -2.2379e-004
B43: -4.9013e-004
B44: -2.9742e-004
B45: -3.6943e-004
Input delays (listed by channel): -5
Estimated using Impulse from data set Data
Loss function and FPE
Sampling interval: 1
Выведем список параметров этой модели командой get(imp):
A: 1
B: [1x1x46 double]
dA: []
dB: []
na: 0
nb: 46
nk: 0
InitialState: 'Auto'
Name: 'imp'
Ts: 1
InputName: {'u1'}
InputUnit: {''}
OutputName: {'y1'}
OutputUnit: {''}
TimeUnit: ''
ParameterVector: [46x1 double]
PName: {}
CovarianceMatrix: []
NoiseVariance: 1
InputDelay: -5
Algorithm: [1x1 struct]
EstimationInfo: [1x1 struct]
Notes: [7x36 char]
UserData: []
Теперь выделяем коэффициенты дискретного фильтра, представляющего линейную модель системы.
[c,d]=th2poly(imp);
Эти коэффициенты можно увидеть выше в сведениях о модели.
Пропускаем через этот фильтр все данные,
Ou1=filter(d,c,In);
plot([Ou1(6:200) Ou(1:195)]);
Мы изобразим графики со смещением, так как в сведениях о модели указано: «Input delays (listed by channel): -5». Результаты сравнения идентификации с реальными данными приведены на рисунке 8:
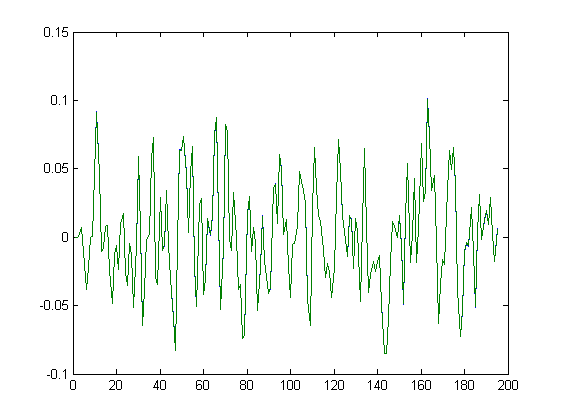
Рисунок 8. Сравнение выхода созданного фильтра и заданного результата.
Оценим среднеквадратичную ошибку фильтра с первого отсчета. Переходного процесса нет, так как мы его устранили, введя задержку сигнала.
Err3=sqrt(sum((Ou1(6:200)-Ou(1:195)).^2)/length(Ou(1:195)))
Err3 = 1.7893e-004
Как мы видим, ошибка получилась маленькая. Однако, с другой стороны, происходит задержка сигнала в этом фильтре, когда первому отсчету на входе соответствует шестой отсчет на выходе.
Сравнение моделей, полученных по половине и по целому набору данных:
Для проведения такого сравнения приведем графики, полученные в результате выполнения следующих команд (рисунка 9, 10):
id=iddata(Ou,In,1);
compare(id,arxqs);
compare(id,imp);

Рисунок 9. Результат моделирования моделью arxqs, полученной по половине данных.
