
- •29. Экстраполяция и интерполяция динамических рядов.
- •30. Аналитические показатели рядов динамики. Методы изучения рядов динамики.
- •1. Основные понятия о рядах динамики
- •2. Виды рядов динамики
- •3. Основные показатели анализа динамических рядов
- •31. Индексный метод анализа, его значение. Виды индексов.
- •Индивидуальные индексы
- •Веса агрегатных индексов цен и физического объема продукции
- •Другие агрегатные индексы
- •32. Индексы переменного, постоянного состава, структурных сдвигов, их взаимосвязь.
- •33. Формы индексов, их взаимосвязь.
- •3. Средние индексы из индивидуальных
- •34. Виды и сущность взаимосвязей социально-экономических явлений.
- •6.1. Причинность, регрессия, корреляция
- •35. Построение уравнения парной регрессии.
- •1.2 Нормальная линейная модель парной регрессии
- •1.3 Альтернативный метод нахождения параметров уравнения парной регрессии
- •1.4 Классический метод наименьших квадратов (мнк) для модели парной регрессии
35. Построение уравнения парной регрессии.
1.1. Регрессионный
анализ заключается в определении
аналитического выражения связи (т.е. в
определении вида функции – линейной,
степенной и т.д.), в котором изменение
одной величины (результативного признака)
обусловлено изменением независимой
величины (факторного признака).
Количественно оценить данную взаимосвязь
можно с помощью построения уравнения
регрессии или регрессионной функции.
Так как получить точное соотношение
между изучаемыми экономическими
показателями практически невозможно,
то в регрессионном анализе в уравнение
связи вводится случайная величина
 .
.
Базисной регрессионной
моделью является модель парной
(однофакторной) линейной регрессии.
Данная регрессионная функция называется
полиномом первой степени и используется
для описания равномерно развивающихся
во времени процессов. Общий вид парного
линейного уравнения регрессии,
описывающего зависимость
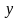 от
от
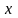 :
:
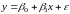 ,
,
где
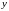 – зависимая переменная,
– зависимая переменная,
 – независимая переменная;
– независимая переменная;
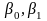 – неизвестные параметры уравнения
регрессии, подлежащие оцениванию;
– неизвестные параметры уравнения
регрессии, подлежащие оцениванию;
– случайная ошибка модели регрессии, появление которой может быть обусловлено следующими объективными предпосылками:
1) нерепрезентативность выборки. В модель парной регрессии включается один фактор, не способный полностью объяснить вариацию результативного признака, который может быть подвержен влиянию множества других факторов в гораздо большей степени;
2) существует вероятность того, что переменные, участвующие в модели, могут быть измерены с ошибкой.
Исходными данными для определения
коэффициентов уравнения регрессии
являются значения зависимой переменной
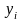 и соответствующие им значения независимой
переменной
и соответствующие им значения независимой
переменной
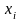 ,
измеренные в
,
измеренные в
 наблюдениях
наблюдениях
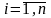 (эмпирические данные)
(эмпирические данные)
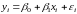 .
.
Аналитическая форма зависимости между изучаемой парой признаков (регрессионная функция) определяется с помощью следующих методов:
на основе визуальной оценки характера связи. На линейном графике по оси абсцисс откладываются значения факторного (независимого) признака , по оси ординат – значения результативного признака . На пересечении соответствующих значений отмечаются точки. Полученный точечный график в указанной системе координат называется корреляционным полем. При соединении полученных точек получается эмпирическая линия, по виду которой можно судить не только о наличии, но и о форме зависимости между изучаемыми переменными;
на основе теоретического и логического анализа природы изучаемых явлений, их социально-экономической сущности.
Параметр
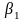 уравнения парной регрессии называется
наклоном. Его величина показывает, на
сколько в среднем изменится результативный
признак
при изменении факторного признака
на единицу своего измерения. Знак
параметра
в уравнении парной регрессии указывает
на направление cвязи. Если
> 0, то связь между изучаемыми показателями
прямая, т. е. с увеличением факторного
признака
увеличивается и результативный признак
,
и наоборот. Если
< 0, то связь между изучаемыми показателями
обратная, т. е. с увеличением фактора
результат
уменьшается, и наоборот.
уравнения парной регрессии называется
наклоном. Его величина показывает, на
сколько в среднем изменится результативный
признак
при изменении факторного признака
на единицу своего измерения. Знак
параметра
в уравнении парной регрессии указывает
на направление cвязи. Если
> 0, то связь между изучаемыми показателями
прямая, т. е. с увеличением факторного
признака
увеличивается и результативный признак
,
и наоборот. Если
< 0, то связь между изучаемыми показателями
обратная, т. е. с увеличением фактора
результат
уменьшается, и наоборот.
Значение параметра
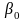 ,
который называется сдвигом, трактуется
как среднее значение результативного
признака упри условии, что факторный
признак
равен нулю. Такая трактовка параметра
возможна только в том случае, если
значение
= 0 имеет смысл.
,
который называется сдвигом, трактуется
как среднее значение результативного
признака упри условии, что факторный
признак
равен нулю. Такая трактовка параметра
возможна только в том случае, если
значение
= 0 имеет смысл.
