; Откуда
. (36)
Натуральное значение фактора х1 опт рассчитывают по уравнению (см. уравнение (2)):
. (37)
Максимум (минимум) параметра Y(Х1 опт) рассчитывается по формуле:
. (38)
Предельная
абсолютная погрешность
рассчитывается по формуле (см. уравнение
(35):
. (39)
6. Если полученное однофакторное ортогонализированное уравнение регрессии второго порядка неадекватно, следует перейти к построению однофакторного ортогонализированного уравнения регрессии третьего порядка.
Типовая задача
Цель типовой задачи: Освоить методы моделирования и оптимизации однофакторных стохастических систем.
Формулировка типовой задачи. Условия задачи полностью совпадают с условиями типовой задачи раздела 2.1. Исходные данные приведены в таблице 11. Так как полученное в разделе 2.1 однофакторное уравнение регрессии первого порядка неадекватно, то перейдём к построению однофакторного ортогонализированного уравнения регрессии второго порядка.
В
связи с тем, что для построения
однофакторного
ортогонализированного
уравнения регрессии второго
порядка
используются те же самые экспериментальные
данные, которые были использованы для
построения однофакторного уравнения
регрессии первого
порядка (тот же РСП, с тем же количеством
опытов
и числом их дублей
),
то рассчитанные по экспериментальным
данным параметры
остаются теми же самыми. Кроме того, так
как многочлены Х0,
Х1
и
ортогональны,
то и параметры уравнения регрессии
второго
порядка
,
остаются такими же и в уравнении регрессии
первого
порядка (см. раздел 2.1, Типовая
задача,
пп. 2 ‑ 6). Поэтому план решения
задачи по построению однофакторного
ортогонализированного
уравнения регрессии второго
порядка
будет содержать только пункты, направленные
на расчет дополнительных параметров,
связанных с появлением ортогонализированного
квадратичного многочлена
.
План решения типовой задачи.
1. Внимательно прочитать условия задачи, осмыслить ее цель, выбрать параметры, которые следует рассчитать.
2. Используя план эксперимента РСП для и соответствующую ему матрицу моделирования (см. раздел 2.1, Типовая задача, пп. 3, 5, таблицы 12, 13) создать матрицу моделирования для построения однофакторного ортогонализированного уравнения регрессии второго порядка и рассчитать коэффициенты .
3.
Произвести статистическую оценку
качества полученного однофакторного
уравнения
регрессии
второго порядка:
значимость регрессионного
коэффициента
на значимость
по критерию Стьюдента,
адекватность уравнения регрессии
по критерию Фишера.
4. Провести оптимизацию изучаемого объекта.
5. По результатам моделирования и оптимизации изучаемого объекта сделать окончательный вывод.
Решение задачи согласно по намеченному плану.
1. Пункт выполнить самостоятельно.
2. Создадим матрицу моделирования для построения однофакторного ортогонализированного уравнения регрессии второго порядка (таблица 22).
2.1.
Рассчитаем ортогонализирующий коэффициент
для числа опытов
:
.
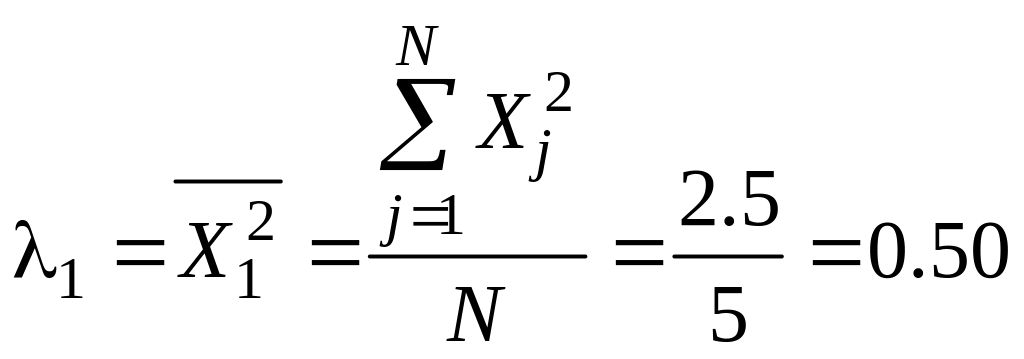2.2. Создадим столбец ортогонализированного многочлена ( ) (внести в таблицу 22).
Например:
.
Перенесем
столбцы факторов
из таблицы 12 в таблицу 22.
Таблица 22. ‑ Матрица моделирования для построения однофакторного
уравнения регрессии второго порядка и результаты обработки данных
N |
X0j |
X1j |
|
|
|
|
|
|
|
1 |
1 |
– 1.0 |
0.50 |
74.10 |
74.10 |
– 74.10 |
37.05 |
73.92 |
0.0324 |
2 |
1 |
– 0.5 |
‑ 0.25 |
61.45 |
61.45 |
–30.725 |
‑ 15.36 |
62.21 |
0.5776 |
3 |
1 |
0 |
‑ 0.50 |
57.00 |
57.00 |
0.00 |
‑ 28.50 |
55.87 |
1.2769 |
4 |
1 |
0.5 |
‑ 0.25 |
54.13 |
54.13 |
27.065 |
‑ 13.53 |
54.90 |
0.5929 |
5 |
1 |
1.0 |
0.50 |
59.48 |
59.48 |
59.48 |
29.74 |
59.30 |
0.0324 |
|
5 |
2.5 |
0.875 |
|
306.2 |
‑ 18.28 |
9.394 |
|
|
Уравнение адекватно |
|
61.24 |
‑ 7.312 |
10.74 |
|
||||
2.3. Убедимся в том,
что факторы
ортогональны многочлену (
),
то есть
и
:
,
.
2.4. Рассчитаем
вспомогательную величину
(результат внести в таблицу 22):
.
2.5.
Вспомогательные величины
и
,
а также значения
перенесем из таблицы 13 в таблицу 22.
2.6. Рассчитаем регрессионный коэффициент для однофакторного ортогонализированного уравнения регрессии второго порядка .
Образуем столбец
и рассчитаем вспомогательную сумму
(результат расчета внести в таблицу
22):
.
Рассчитаем коэффициент :
.
4. Произведём статистическую оценку качества полученного однофакторного уравнения регрессии второго порядка.
4.1. Проверим регрессионный коэффициент на значимость по критерию Стьюдента:
‑ рассчитаем
дисперсию значимости
(с учетом того, что
):
,
.
‑ рассчитаем
доверительный интервал коэффициента
.
,
где
‑ значение
критерия Стьюдента при числе степеней
свободы
и доверительной вероятности
выбирается из таблицы Приложения 2.
Следовательно, коэффициент значим, так как:
Вывод: все три коэффициента ортогонализированного однофакторного уравнения регрессии второго порядка значимы.
С учетом правил корректной записи результатов расчета (см. раздел 1.1, Кратко теория, п.4) запишем значение коэффициента (внести в таблицу 22):
4.2. Проверим однофакторное уравнение регрессии второго порядка на адекватность по критерию Фишера:
‑ рассчитаем
столбец параметра
в
каждом опыте по однофакторному
ортогонализированному
уравнению регрессии второго
порядка
(результаты расчета внести в таблицу
22). Например:
.
‑ рассчитаем значения столбца (результаты расчета внести в таблицу 22). Например:
.
‑ рассчитаем остаточную сумму квадратов (результат расчёта внести в таблицу 22):
‑ рассчитаем дисперсию адекватности и число её степеней свободы fад:
,
.
‑ рассчитаем экспериментальное значение критерия Фишера:
,
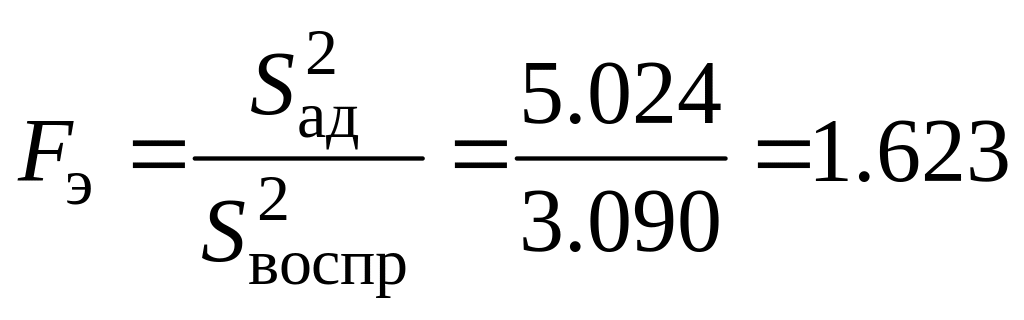так как
;
‑ критическое
значение критерия Фишера при числах
степеней свободы 
, 
и доверительной вероятности р = 0.95
выберем из таблицы Приложения 4:
.
С учетом доверительных интервалов и правила округления коэффициенты запишем в следующем виде (раздел 1.1, Кратко теория, п. 4):
,
,
Вывод: Полученное однофакторное ортогонализированное уравнение регрессии второго порядка
адекватно, так как
.
5. Проведем оптимизацию изучаемого объекта:
6.1. Параметр Y(Х1)
достигает минимум, так как
.
Необходимое условие минимума
.
Рассчитаем оптимальное значение фактора
:
,
.
Оптимальное
значение фактора
равно:
.
6.2. Рассчитаем минимальное значение изучаемого параметра Ymin:
6.3. Абсолютную
и относительную погрешность
параметра
Ymin,
значение которого определили по
однофакторному
ортогонализированному
уравнению регрессии второго
порядка
,
рассчитаем по формулам:
кВтч/т.
.
С учетом правил
округления результатов расчета (раздел
1.1, Кратко теория, п. 4)
.
7.
Окончательный вывод. Однофакторное
ортогонализированное
уравнение регрессии второго
порядка со значимыми регрессионными
коэффициентами
адекватно описывает изучаемый объект.
Минимальные энергозатраты при сушке
зерна
достигаются при температуре воздуха
.
Пример оформления ответа для типовой задачи.
1. Ортогонализированное однофакторное уравнение регрессии второго порядка
, кВтч/т.
0.8 1.2 2.0
, ;
,
;
,
,
Однофакторное ортогонализированное уравнение регрессии второго порядка адекватно, так как:
.
2. Оптимальные параметры ,
,
,
.
Контрольные вопросы к задаче
Блок А.
1. Написать в общем виде однофакторное уравнение регрессии первого порядка.
2. Написать формулы взаимосвязи нормированных Х1 и натуральных х1 значений фактора.
3. Построить равномерно-симметричный план (РСП) для N = 11.
4. Построить равномерно-симметричный план (РСП) для N = 21.
5. Доказать, что
для РСП факторы Х0,
и Х1
ортогональны для любого
.
6. Какие операции включает в себя предварительная обработка экспериментальных данных?
7. Написать формулу для расчета выборочного среднего в каждом опыте .
8. Написать формулу для расчета выборочной дисперсии в каждом опыте .
9. Сформулировать алгоритм проверки всех выборочных дисперсий на однородность.
10. Как найти табличное значение критерия Кохрена?
11. Написать формулу для расчета дисперсии воспроизводимости и числа её степеней свободы.
12. Написать формулы для расчета коэффициентов однофакторного уравнения регрессии первого порядка.
13. Написать формулы для расчета дисперсий значимости коэффициентов однофакторного уравнения регрессии первого порядка.
14. Написать формулы для расчета доверительных интервалов коэффициентов однофакторного уравнения регрессии первого порядка. Сформулировать критерий для проверки регрессионных коэффициентов на значимость.
15. Как найти табличное значение критерия Стьюдента?
16. Написать уравнение для расчета дисперсии адекватности и числа её степени свободы.
17. Сформулировать алгоритм проверки уравнения регрессии любого порядка на адекватность.
18. Как найти табличное значение критерия Фишера?
Блок Б.
1. Написать в общем виде однофакторное уравнение регрессии первого порядка и ортогонализированное однофакторное уравнение регрессии второго порядка.
2. Написать формулу
для расчета ортогонализирующего
коэффициента
.
3. Написать формулы взаимосвязи нормированных Х1 и натуральных х1 значений фактора.
4. Построить матрицу моделирования для построения ортогонализированное однофакторное уравнение регрессии второго порядка на основе РСП для N = 11.
5. Доказать, что в
матрице моделирования для построения
ортогонализированного
однофакторного
уравнения регрессии второго
порядка многочлены Х0,
Х1
и
ортогональны.
6. Какие операции включает в себя предварительная обработка экспериментальных данных?
7. Написать формулу для расчета выборочного среднего в каждом опыте .
8. Написать формулу
для расчета выборочной дисперсии
и её числа степеней свободы
в
каждом опыте.
9. Сформулировать алгоритм проверки всех выборочных дисперсий на однородность.
10. Как найти табличное значение критерия Кохрена?
11. Написать формулу для расчета дисперсии воспроизводимости и числа её степеней свободы.
12. Написать формулы для расчета коэффициентов ортогонализированного однофакторного уравнения регрессии второго порядка.
13. Написать формулы для расчета дисперсий значимости коэффициентов ортогонализированного однофакторного уравнения регрессии второго порядка.
14. Написать формулы для расчета доверительных интервалов коэффициентов ортогонализированного однофакторного уравнения регрессии второго порядка. Сформулировать критерий для проверки регрессионных коэффициентов на значимость.
15. Как найти табличное значение критерия Стьюдента?
16. Написать уравнение для расчета дисперсии адекватности и числа её степени свободы.
17. Сформулировать алгоритм проверки уравнения регрессии любого порядка на адекватность.
18. Как найти табличное значение критерия Фишера?
19. Написать уравнение для расчета абсолютной погрешности Y(Х1) параметра Y(Х1), рассчитанного по ортогонализированному однофакторному уравнению регрессии второго порядка .
20. Сформулировать алгоритм оптимизации изучаемого объекта, описываемого ортогонализированным однофакторным уравнением регрессии второго порядка.