5.3. Проверка однофакторного уравнения регрессии первого порядка на адекватность.

Дисперсия адекватности и число её степеней свободы для однофакторного уравнения регрессии первого порядка равны:

, (22)

, (23)

где n – число дублей в каждом опыте;  ‑ остаточная сумма квадратов;  ‑ расчетные значения параметра Y, полученные по однофакторному уравнению регрессии первого порядка ( ), в котором оставлены только значимые коэффициенты; N ‑ число опытов; В ‑ число значимых коэффициентов однофакторного уравнения регрессии первого порядка.

Адекватность уравнения регрессии, которое характеризуется с числом степеней свободы и с числом степеней свободы , проверяется по критерию Фишера:

‑ экспериментальное значение критерия Фишера F_э, (отношение большей выборочной дисперсии к меньшей):

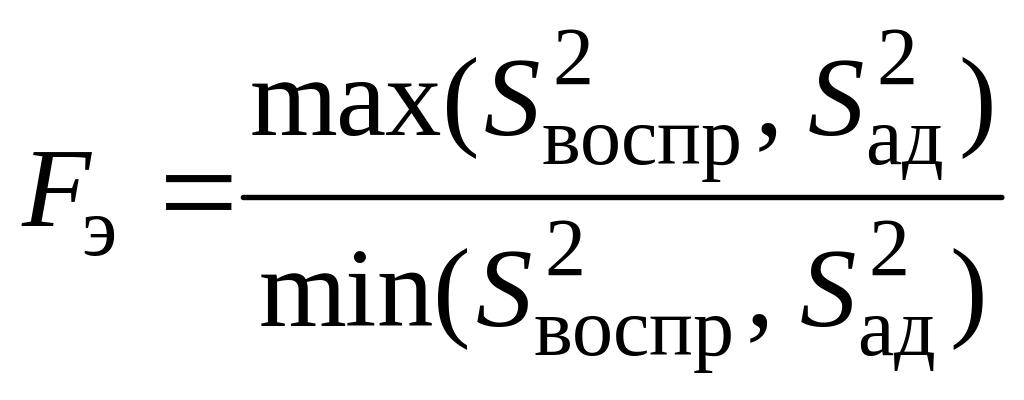, (24)

‑ табличное значение критерия Фишера , где  ‑ число степеней свободы большей дисперсии,  ‑ число степеней свободы меньшей дисперсии, выбирается из таблицы Приложения 4;

‑ критерий адекватности уравнения регрессии (равносильно критерию однородности 2-х дисперсий на однородность):

‑ уравнение регрессии с доверительной вероятностью р адекватно, то есть , если:

, (25)

‑ уравнение с доверительной вероятностью р неадекватно ( ), если:

. (26)

6.4. Предельная абсолютная погрешность параметра Y(Х₁), рассчитанного по однофакторному уравнению регрессии первого порядка , в случае его адекватности определяется по формуле:

, (27)

где  ‑ табличное значение критерия Стьюдента при числе степеней свободы и доверительной вероятности р находится из таблицы Приложения 2.

6. Если полученное однофакторное уравнение регрессии первого порядка неадекватно, следует перейти к построению уравнению регрессии второго порядка.

Типовая задача (вариант № 30).

Цель: Освоить методы моделирования и оптимизации однофакторных стохастических систем.

Формулировка задачи. Зерно, собранное комбайном в поле, имеет влажность  30 %. На току при естественной сушке зерно высыхает до влажности  20 %. Однако для долгосрочного хранения зерна на элеваторе зерно должно иметь влажность 14 %. До этой влажности зерно доводят в специальных сушилах, теплоносителем в которых является горячий воздух.

Важнейшим параметром, характеризующим эффективность работы сушила, является удельный расход энергии (энергия на тонну высушенного зерна). При прочих равных условиях удельный расход энергии (параметр Y, кВтч/т) зависит от температуры теплоносителя (фактор х₁,С ). В данной задаче изучалась зависимость удельного расхода энергии Y от температуры теплоносителя х₁, которая варьировалась в диапазоне:   С.

Математическая формулировка задачи: 1) построить адекватное уравнение регрессии, отражающее зависимость удельного расхода энергии (параметр Y, кВтч/т) от температуры воздуха (фактор х₁ С); 2) рассчитать оптимальное значение фактора х₁(С), при котором удельный расход энергии Y будет минимальным.

Моделирование изучаемой системы начнем с построения однофакторного уравнения регрессии первого порядка. В качестве плана эксперимента возьмем РСП с числом опытов и числом дублей . Результаты эксперимента представлены в таблице 1.

Таблица 1. ‑ Экспериментальные данные для РСП.

N	х1j, С	Yj1, кВтч/т	Yj2, кВтч/т	Yj3, кВтч/т	Yj4, кВтч/т
1	60	73.5	75.3	73.5	74.1
2	75	60.4	60.2	63.7	61.5
3	90	55.4	59.0	58.8	54.8
4	105	54.8	55.5	54.3	51.9
5	120	59.7	62.5	57.9	57.8

План решения задачи.

1. Внимательно прочитать условия задачи.

2. Выполнить переход от натуральных значений фактора х₁ к нормированным Х₁.

3. Создать матрицу планирования эксперимента и выполнить предварительную обработку экспериментальных данных.

4. Создать матрицу моделирования и рассчитать коэффициенты .

5. Произвести статистическую оценку качества полученного однофакторного уравнения регрессии первого порядка (значимость коэффициентов регрессии, адекватность уравнения регрессии).

6. Принять решение о дальнейшем пути исследования изучаемого объекта.

NB!!! Все предварительные расчёты проводить до минимум 4-х значащих цифр.

Решение задачи согласно плану.

1. Пункт плана 1 выполнить самостоятельно.

2. Уровни и интервал варьирования фактора, а также формулы перевода натуральных x₁ в нормированные X₁ и обратно приведены в таблице 2 (см. уравнения (1) – (4)).

Таблица 2. – Уровни и интервал варьирования фактора x₁ (X₁).

Факторы	1-й фактор (семена)
	x1, С	X1
Нижний уровень	x1 max = 120	+ 1
Верхний уровень	x1 min = 60	‑ 1
Основной уровень	x10 = 90	0
Интервал варьирования	x1 = 30
Формулы перевода натуральных x1 в нормированные X1 и обратно	;

3. Создадим матрицу планирования на базе равномерного симметричного плана (РСП), внесём в неё экспериментальные данные из таблицы 1 и проведём предварительную обработку экспериментальных данных (таблица 3) (см. раздел А, п. 3).

Таблица 3. – Матрица планирования на базе РСП для ,

и результаты предварительной обработки данных

N		Yj1,кВтч/т	Yj2,кВтч/т	Yj3,кВтч/т	Yj4,кВтч/т
1	60	73.5	75.3	73.5	74.1	74.10	0.7200
2	75	60.4	60.2	63.7	61.5	61.45	2.5767
3	90	55.4	59.0	58.8	54.8	57.00	4.8800
4	105	54.8	55.5	54.3	51.9	54.13	2.4425
5	120	59.7	62.5	57.9	57.8	59.48	4.8292

3.1. Методика эксперимента. Для повышения точности определения параметра эксперимент проводится в сушиле, оборудованном средствами автоматизации для поддержания основного фактора ‑ температуры теплоносителя (воздух) ( ) на требуемом уровне с точностью С. Другие факторы, такие как объёмный расход воздуха, влажность воздуха, линейная скорость воздуха относительно зерна, также измеряются датчиками и помощью средств автоматизации поддерживаются на фиксированных уровнях. Влажность высушенного зерна поддерживалась на требуемом уровне  %. Если влажность зерна становилась больше 14 %, то скорость конвейерной ленты соответственно увеличивалась, если влажность зерна становилась меньше 14 %, то скорость конвейерной ленты соответственно уменьшалась. Каждые 2 ч по счетчику электроэнергии с относительной погрешностью 0.1 % определялась величина электроэнергии, затраченной на проведение эксперимента (энергия на подогрев воздуха; энергия компрессора на обдув зерна воздухом; энергия двигателя на движение конвейерной ленты). За этот же период времени измерялась масса высушенного зерна с относительной погрешностью 0.1 %. Параметр определялся как отношение затраченной электроэнергии (кВтч) за 2 часа к массе высушенного зерна (т) за этот же период. Таким образом, за одну смену (8 ч) при заданной температуре теплоносителя параметр  определялся 4 раза ( . Полностью определение зависимости параметра от температуры теплоносителя осуществлялась за 5 дней ( ) при температурах 60, 75, 90, 105 и 120 С.

3.2. Проведем предварительную обработку экспериментальных данных (результаты расчета внести в таблицу 3).

Выборочное среднее в каждом опыте (см. уравнение (6)):

, .

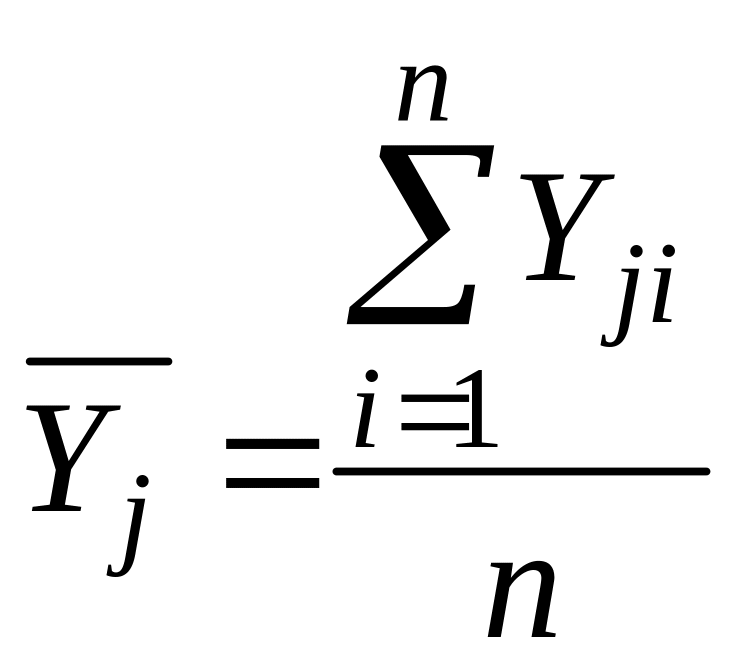Например, выборочное среднее в третьем опыте ( ):

.

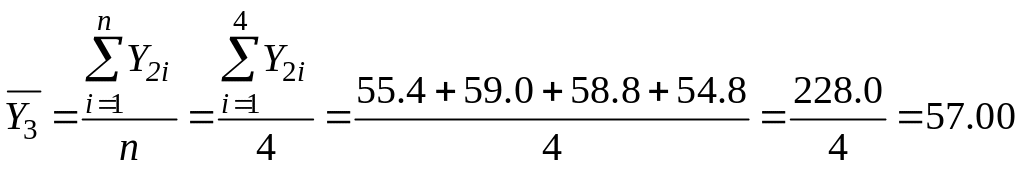Выборочная дисперсия в каждом опыте (см. уравнение (7)):

, .

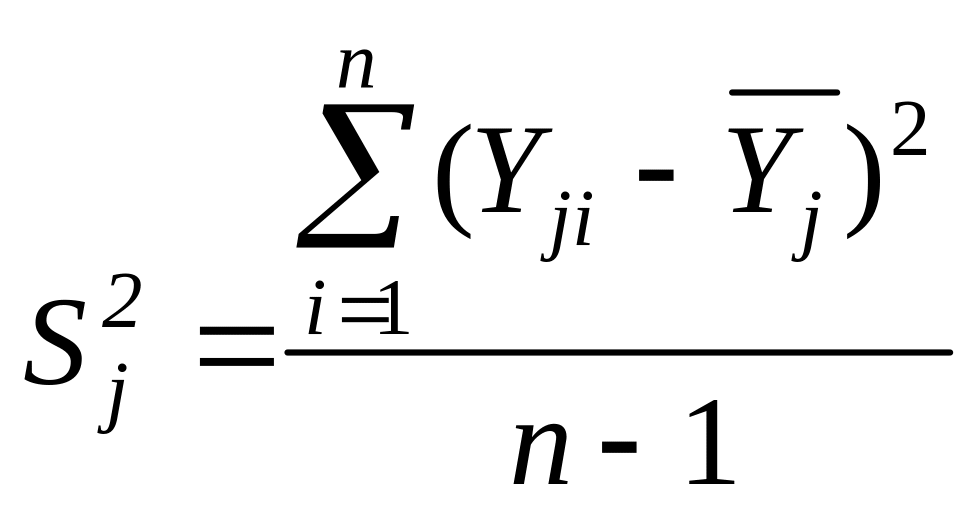Например, выборочная дисперсия в третьем опыте ( ):

.

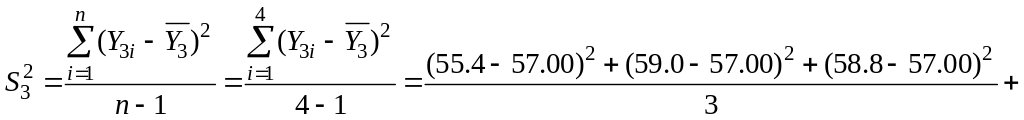
Однородность выборочных дисперсий по критерию Кохрена (см. уравнения (8)):

‑ экспериментальное значение критерия Кохрена G_э :

;

‑ табличное значение критерия Кохрена  при , и доверительной вероятности р = 0.95 выбирается из таблицы Приложения 5:

.

Вывод: выборочные дисперсии однородны, так как (см. уравнение (9)).

Дисперсия воспроизводимости и её число степеней свободы (см. уравнение (11) – (12)):

,

.
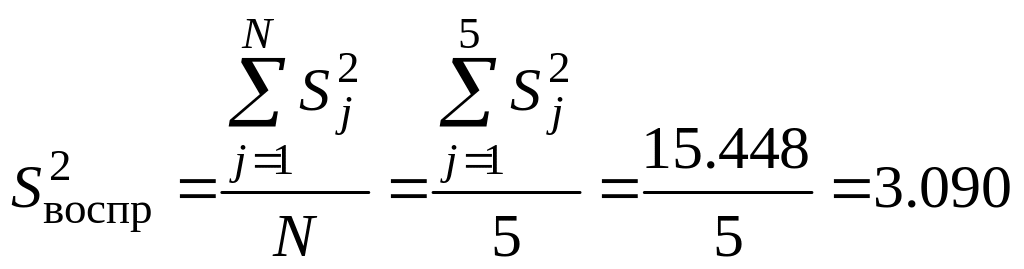