8. Электростатическое поле точечного заряда

9. Электрическое поле заряженной нити

Поток через эту поверхность складывается из потока через боковую поверхность и потоков через два основания цилиндра:

Но потоки через основания цилиндра равны нулю, так как эти основания параллельны линиям . На боковой поверхности цилиндра ׀׀ .

Тогда

Гауссова поверхность заключает в себе заряд .

По теореме Гаусса , тогда получим .

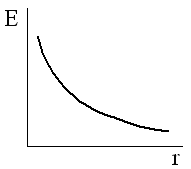
Таким образом, напряженность поля, созданного заряженной нитью, убывает обратно пропорционально расстоянию от нити.

10. Электрическое поле заряженной плоскости

11. Электрическое поле плоского конденсатора

12. Электрическое поле заряженной сферы

По поверхности.

Электрическое поле равномерно заряженной сферы симметрично относительно её центра; значит геометрическое место точек, в которых модули напряженности одинаковы, представляет собой тоже сферу, центр которой совпадает с центром заряженной сферы. Следовательно, в качестве гауссовой поверхности следует выбрать сферу радиуса r.

1. r≥ R. Так как ║‌‌‌ во всех точках гауссовой поверхности, то

Внутрь этой гауссовой поверхности попадает весь заряд, создающий поле.

По теореме Гаусса .

Приравняем правые части равенств и получим , а в точках, лежащих на поверхности заряженной сферы (r = R) ,

2. r<R. Т.к. внутри гауссовой сферы теперь нет зарядов, все они, по условию, распределены по поверхности радиуса R, то N=ES=0. Отсюда E=0.Как следует из полученных расчетов, внутри сферы поле отсутствует, при переходе через заряженную поверхность напряженность скачком возрастает до максимального значения и затем убывает обратно пропорционально квадрату расстояния от центра сферы.

По объёму.

1. также как и в 1. по поверхности.

1. r<R. В этом случае поток вектора напряженности через поверхность гауссовой сферы также равен , а заряд, попавший внутрь этой сферы равен теперь .

Приравнивая правые части равенств, получим , отсюда

.

Таким образом, напряженность поля внутри сферы линейно возрастает от нуля до максимального значения на поверхности сферы, а затем вне сферы убывает обратно пропорционально квадрату расстояния от ее центра

13. Электрическое поле заряженного шара

14. Энергия системы точеных зарядов

Электростатические силы взаимодействия консервативны, следовательно, система зарядов обладает потенциальной энергией. Рассмотрим потенциальную энергию системы двух неподвижных точечных зарядов q1 и q2, находящихся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией.

Где ₁₂ и ₂₁ - потенциалы, создаваемые зарядом q₂ в точке нахождения заряда q₁ и зарядом q₁ в точке нахождения заряда q₂.

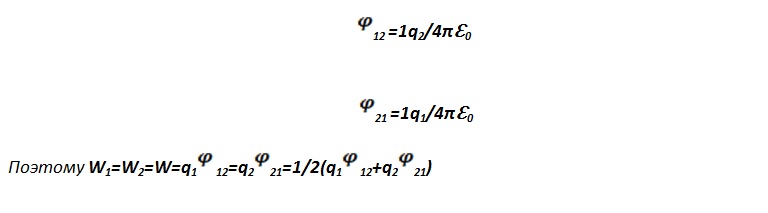
Добавляя к системе из двух зарядов последовательно заряды q₃, q₄,…, можно убедиться в том, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна

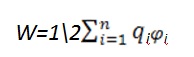
Где _i – потенциал, создаваемый в той точке, где находится заряд q_{i .}