
- •Цели и задачи сопротивления материалов
- •Внешние и внутренние силы
- •Нормальные и касательные напряжения
- •Линейное (одноосное) напряженное состояние
- •Плоское (двухосное) напряженное состояние
- •Главные напряжения
- •Траектории главных напряжений и траектории наибольших касательных напряжений
- •Трехосное (пространственное) напряженное состояние
- •Круги Мора для трехосного напряженного состояния
- •Дифференциальные уравнения равновесия элементарного объема тела
Трехосное (пространственное) напряженное состояние
Для определения
пространственного (трехосного)
напряженного состояния надо знать шесть
величин, а именно – нормальные и
касательные напряжения на трех взаимно
перпендикулярных площадках. Нормальные
напряжения
,
,
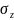 считаются положительными, если они
направлены наружу от соответствующих
площадок. Касательные напряжения на
каждой площадке определяются двумя
компонентами и обозначаются буквой
,
где индекс i
будет указывать направление нормали к
той грани, на которой касательное
напряжение действует, а индекс j
будет указывать направление самого
касательного напряжения. Следовательно,
для трех площадок получается девять
величин. Но вследствие равенства
касательных на каждых двух взаимно
перпендикулярных площадках имеем:
считаются положительными, если они
направлены наружу от соответствующих
площадок. Касательные напряжения на
каждой площадке определяются двумя
компонентами и обозначаются буквой
,
где индекс i
будет указывать направление нормали к
той грани, на которой касательное
напряжение действует, а индекс j
будет указывать направление самого
касательного напряжения. Следовательно,
для трех площадок получается девять
величин. Но вследствие равенства
касательных на каждых двух взаимно
перпендикулярных площадках имеем:
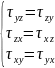
Поэтому остается только шесть величин.
Расположим девять величин
,
,
,
,
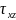 ,
,
,
,
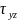 ,
,
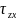 ,
,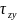 в виде симметричной матрицы:
в виде симметричной матрицы:
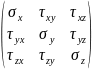
И будем ее называть пространственным тензором напряжений. Вследствие равенства касательных на каждых двух взаимно перпендикулярных площадках, для определения пространственного тензора напряжений достаточно знать только шесть его компонентов , , , , , .
Покажем, что через эти
шесть величин, определяющих направление
на трех взаимно перпендикулярных
площадках, можно выразить напряжения
на любой другой площадке. Для этого
рассмотрим элементарный объем в форме
тетраэдра на рис.9, ребра которого,
сходящиеся в начале координат, взаимно
перпендикулярны и направлены по осям
координат х, у, z. Пусть нормаль
к наклонной площадке АВС, направленная
наружу, имеет направляющие косинусы λ,
μ, ν, и
пусть площадь АВС равна
.
Компоненты полного напряжения р,
действующего на наклонной площадке,
обозначим через
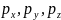 .
В направлении оси х на боковых гранях
тетраэдра действуют следующие напряжения:
.
В направлении оси х на боковых гранях
тетраэдра действуют следующие напряжения:
На грани ОВС – нормальное
напряжение
,
на грани ОСА – касательное напряжение
и на грани ОАВ – касательное напряжение
.
Замечая, что площади граней ОВС, ОСА и
ОАВ равны соответственно
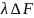 ,
,
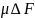 и
и
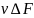 ,
получим из условия равновесия тетраэдра
в направлении оси х первое уравнение
системы:
,
получим из условия равновесия тетраэдра
в направлении оси х первое уравнение
системы:
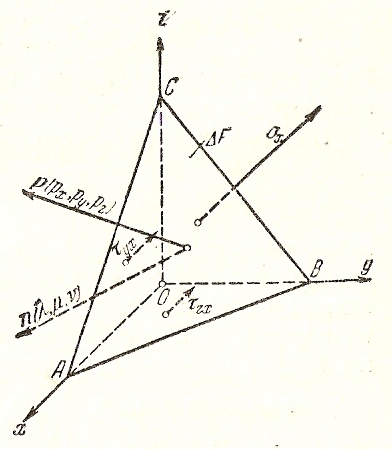 Рис.9
Рис.9
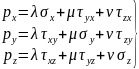
Второе и третье уравнение получаются аналогично из условий равновесия в направлении осей у и z.
Подставляя в равенство
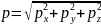 найденные значения
найденные значения
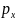 ,
,
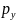 ,
,
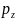 можно получить абсолютное значение
полного напряжения на наклонной площадке
АВС, выраженное через компоненты тензора
напряжений. Проектируя р
на нормаль n
или составляя сумму проекций
,
,
на нормаль, найдем нормальное напряжение
σ:
можно получить абсолютное значение
полного напряжения на наклонной площадке
АВС, выраженное через компоненты тензора
напряжений. Проектируя р
на нормаль n
или составляя сумму проекций
,
,
на нормаль, найдем нормальное напряжение
σ:
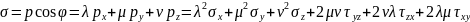
Касательное напряжение на площадке АВС равно
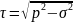
При трехосном напряженном состоянии в каждой точке тела имеются три взаимно перпендикулярные плоскости, в которых касательные напряжения отсутствуют, следовательно, вектор полного напряжения для каждой из этих плоскостей перпендикулярен к ней. Эти плоскости называются главными, а действующие на них напряжения – главными напряжениями. Прямые линии, по которым пересекаются главные плоскости напряженного состояния, называются главными направлениями напряженного состояния.
