5. Плоское (двухосное) напряженное состояние

Напряженное состояние, при котором векторы полных напряжений лежат в одной и той же плоскости, называется плоским или двухосным. Такое напряженное состояние приближенно осуществляется в тонких пластинках, нагруженных силами только в своей плоскости, а также в телах цилиндрической формы, в которых напряжения изменяются вдоль образующей (в этом случае во всех плоскостях, перпендикулярных к образующей, имеют место одинаковые двухосные напряженные состояния).

Теорема: В каждых двух взаимно перпендикулярных плоскостях компоненты касательных напряжений, направленные перпендикулярно к линии пересечения этих плоскостей, равны между собой и при этом направлены либо оба к линии пересечения, либо оба от линии пересечения. Эта теорема справедлива для двухосного и трехосного напряженного состояния.

Рассмотрим частицу тела в форме прямоугольного параллелепипеда со сторонами , , (рис.6), расположенными вдоль осей х, у, z прямоугольной системы координат. Компоненты касательных напряжений, действующие на боковых гранях этого параллелепипеда, будем обозначать буквой с двумя индексами. Причем индекс i будет указывать направление нормали к той грани, на которой касательное напряжение действует, а индекс j будет указывать направление самого касательного напряжения.

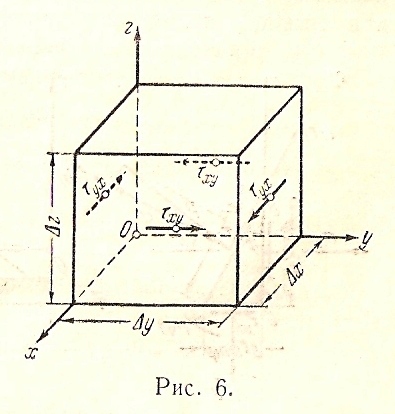
На рис.6 показаны касательные напряжения, действующие на боковых гранях параллелепипеда параллельно плоскости ху. Касательные напряжения перпендикулярные плоскости ху, не показаны, так как они не дают моментов относительно оси z. Для равновесия параллелепипеда необходимо, чтобы сумма моментов действующих на него относительно любой оси и относительно оси z, равнялась нулю. Это условие приводит к уравнению

Откуда получаем, что:

Так как взятые плоскости не отличаются от других плоскостей, то теорема доказана для любых пар взаимно перпендикулярных плоскостей.

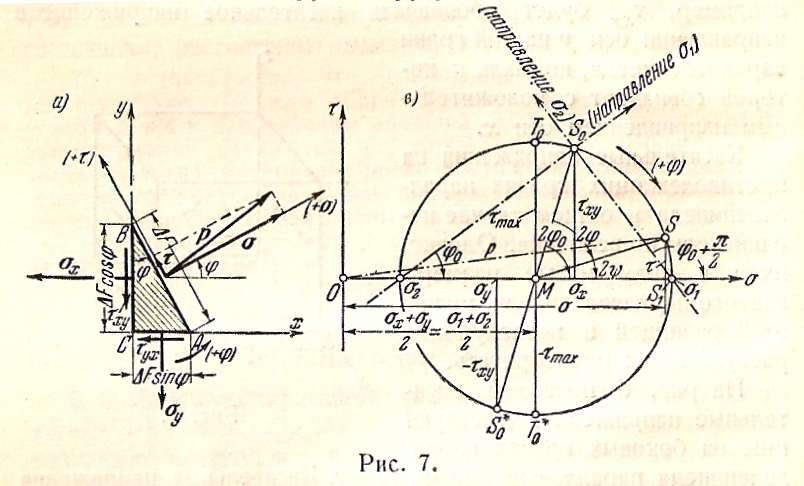
Рассмотрим тело в плоском напряженном состоянии. Плоскость, в которой лежат векторы полных напряжений , совместим с плоскостью рисунка и будем рассматривать напряжения только на тех элементарных площадках, которые перпендикулярны к плоскости рисунка. Проведем площадки ВС и СА, перпендикулярные друг к другу. Пусть нормальные напряжения на этих площадках равны и , а касательные напряжения и . Напишем эти величины в виде матрицы:

И назовем совокупность таких четырех величин плоским тензором напряжений.

Отдельные члены тензора будем называть его компонентами. Так как , то для определения плоского тензора напряжений достаточно знать величину трех его компонентов.

Напряжение на площадке ВС следует считать положительным, а напряжение на площадке СА отрицательным.

Площадки ВС, СА и АB выделяют в рассматриваемом теле маленькую призму АВС. Пусть площадь грани AВ равна . Тогда площадь грани ВС будет , а площадь грани СА будет . Условия равновесия призмы для направлений + и + приводят к уравнениям:

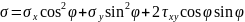
Или после введения удвоенного угла 2φ:

Исключив отсюда φ, получим уравнение:

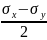Таким образом, при плоском напряженном состоянии значения и , которые могут принимать нормальные и касательные напряжения, ограничиваются значениями координат точек лежащих на окружности. Круг, ограниченный этой окружностью, называется круговой диаграммой Мора, положение его центра определяется отрезком , а радиус – гипотенузой треугольника, потроенного на катетах и (рис.7).