
- •Экзаменационные вопросы по высшей математике
- •3. Найдите общее решение дифференциального уравнения
- •2. Найдите общее решение дифференциального уравнения
- •3. Найти интервал сходимости степенного ряда
- •2. Найдите общее решение дифференциального уравнения
- •2. Найдите общее решение дифференциального уравнения
- •3. Найдите общее решение дифференциального уравнения
- •3. Найдите общее решение дифференциального уравнения
- •2. Дано линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами . Найти частное решение, удовлетворяющее указанным начальным условиям ,
- •3. Дано линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами . Найти частное решение, удовлетворяющее указанным начальным условиям ,
- •2. Дано линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами . Найти частное решение, удовлетворяющее указанным начальным условиям ,
Экзаменационные вопросы по высшей математике
1. Геометрический и физический смысл двойного интеграла
2.
Дан числовой ряд
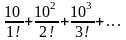 .
Исследуйте сходимость ряда
.
Исследуйте сходимость ряда
3.
Найдите
общее решение дифференциального
уравнения
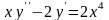
1. Основные свойства двойного интеграла
2.
Исследовать на сходимость числовой ряд
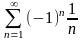
3.
Дано линейное однородное дифференциальное
уравнение второго порядка с постоянными
коэффициентами
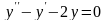 .
Найти частное решение, удовлетворяющее
указанным начальным условиям
.
Найти частное решение, удовлетворяющее
указанным начальным условиям
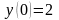 ,
,
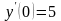
1. Замена переменных в двойном интеграле:
a). Якобиан преобразования G в D;
b). Двойной интеграл в криволинейных координатах;
c). Формула замены переменных при переходе к полярным координатам. В каких случаях удобно переходить к полярным координатам?
2.
Найдите
общее решение дифференциального
уравнения
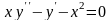
3.
Данный числовой ряд
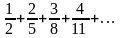 исследовать на сходимость
исследовать на сходимость
1. Приложения двойного интеграла:
а). Формула вычисления объема цилиндрического тела;
b). Формула вычисления площади плоской фигуры;
c). Формула вычисления массы плоской фигуры.
2.
Найдите
общее решение дифференциального
уравнения
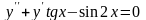
3.
Исследовать на сходимость числовой ряд
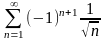
1. Приложения двойного интеграла
a). Формулы вычисления статических моментов фигуры D относительно осей Ох и Оy;
b). Формулы нахождения координат центра масс фигуры D;
c). Чему равен момент инерции фигуры относительно начала координат?
2.
Найдите
общее решение дифференциального
уравнения
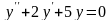
3.
Исследовать на сходимость числовой ряд
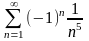
1. Криволинейный интеграл I рода
а). Определение криволинейного интеграла I рода;
b). Определение гладкой кривой;
c). Условие существования криволинейного интеграла I рода.
2.
Данный числовой ряд
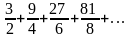 исследовать на сходимость
исследовать на сходимость
3.
Найдите
общий интеграл дифференциального
уравнения
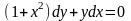
1. Свойства криволинейного интеграла I рода
2.
Найдите общее решение уравнения
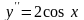
3.
Найти интервал сходимости степенного
ряда
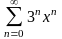
1. Криволинейный интеграл I рода
а). Формула вычисления криволинейного интеграла I рода, если кривая интегрирования представлена в параметрической форме;
b). Формула вычисления криволинейного интеграл I рода, если кривая интегрирования представлена в явном виде;
с). Формула вычисления криволинейного интеграл I рода, если кривая интегрирования задана уравнением в полярных координатах.
2.
Дан числовой ряд
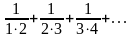 .
Найдите сумму ряда
.
Найдите сумму ряда
3. Найдите общее решение дифференциального уравнения
1. Приложения криволинейного интеграла I рода
а). Чему равна площадь цилиндрической поверхности с направляющей L и образующей, параллельной оси Oz и заключенной между L и поверхностью z = f (x, y)?
b).
Чему равна масса материальной кривой
L
= AB
, имеющая плотность, равную
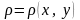 ?
?
2. Найдите общее решение дифференциального уравнения
3. Найти интервал сходимости степенного ряда
1. Криволинейный интеграл II рода
a). Решение, какой задачи приводит к понятию криволинейного интеграла II рода?
b).
Каким равенством определяется
криволинейный интеграл II
рода общего вида
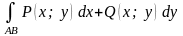 ?
?
2.
Найдите область сходимости ряда

3. .В вазе стоят 9 красных и 7 розовых гвоздик. Сколькими способами можно выбрать из нее 4 красных и 3 розовых гвоздики?
1. Криволинейный интеграл II рода
a). Если кривая АВ задана параметрическими уравнениями, то чему равен интеграл ?
b).
Если кривая АВ
представлена в явном виде непрерывно
дифференцируемой функцией
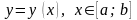 ,
тогда интеграл
определяется равенством
,
тогда интеграл
определяется равенством
