Навчальні завдання

1. Знайти ортогональні траєкторії гіпербол

 Складемо ДР сім’ї гіпербол. Виключимо С з рівняння Диференціюємо рівняння за х:

Для ортогональних ліній Приходимо до ДР:

.

Знаходимо сім’ю ортогональних ліній

2. Знайдемо закон розпаду радіоактивної речовини.

 Позначимо через масу радіоактивної речовини. За час розпадається кількість речовини пропорційна до маси

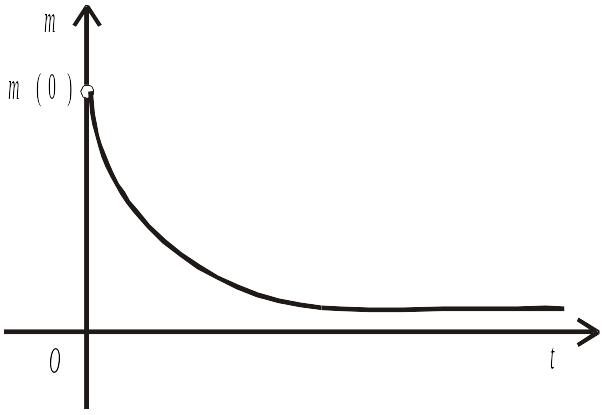
Рис. 8.4

і часу , тобто або При знаходимо ДР з відокремленими змінними:

При t = 0 дістаємо: m (0) = C, .

Маємо експоненціальний закон розпаду радіоактивної речовини.

3. Знайдемо розв’язок однорідного ДР .

 ДР можна записати у вигляді , .

Вводимо нову змінну , y = ux:

, ,

, ,

, , .

4. Знайдемо розв’язок ДР у повних диференціалах.

 , , .

Рівняння можна подати у вигляді .

Звідси знаходимо інтеграл ДР .

5. Розв’яжемо лінійне ДР з початковими умовами х₀ = 1, у₀ = 1:

.

 1. Шукаємо розв’язок за методом Бернуллі:

Зводимо рівняння до системи ДР:

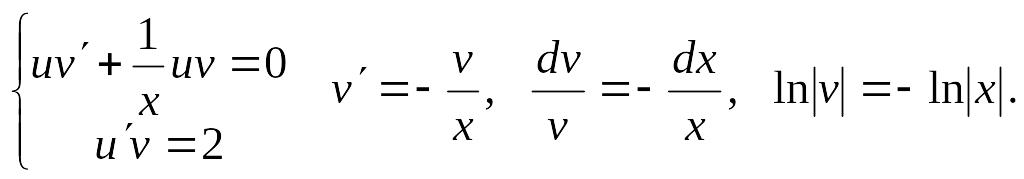
2. Знайдемо розв’язок за методом Лагранжа. Розв’яжемо однорідне рівняння:

, , , , .

Розв’язок неоднорідного ДР шукаємо у вигляді :

, , .

Загальний розв’язок має вигляд .

3. Розв’яжемо ДР за методом Ейлера. Помножимо рівняння на інтегрувальний множник :

. Нехай , , , .

Дістанемо ДР у повних диференціалах

, , , .

Маючи загальний розв’язок, знаходимо частинний розв’язок, що задовольняє початкові умови:

, ; 1 + С = 1, С = 0, у = х.

6. Знайдемо розв’язок ДР Бернуллі , .

 Візьмемо , , .

Знайдемо розв’язок лінійного ДР за методом Бернуллі. Нехай

Записуємо систему ДР:

,

, , , , .

Остаточно маємо шуканий розв’язок: .

Завдання для перевірки знань

Розв’язати диференціальні рівняння:

1. . Відповідь. .

2. . Відповідь. .

3. ; при . Відповідь. .

4. . Відповідь. .

5. . Відповідь. .

6. . Відповідь.

7. . Відповідь. .

8. . Відповідь. .

9. ; при . Відповідь.

10. . Відповідь. .

11. ; при . Відповідь. .

12. . Відповідь.

13. . Відповідь. .

14. . Відповідь. .

15. . Відповідь.

16. . Відповідь. .

17. . Відповідь. .

Завдання для самостійної роботи: № 1-3; 7; 8; 9.