Завдання для перевірки знань
На еліпсі
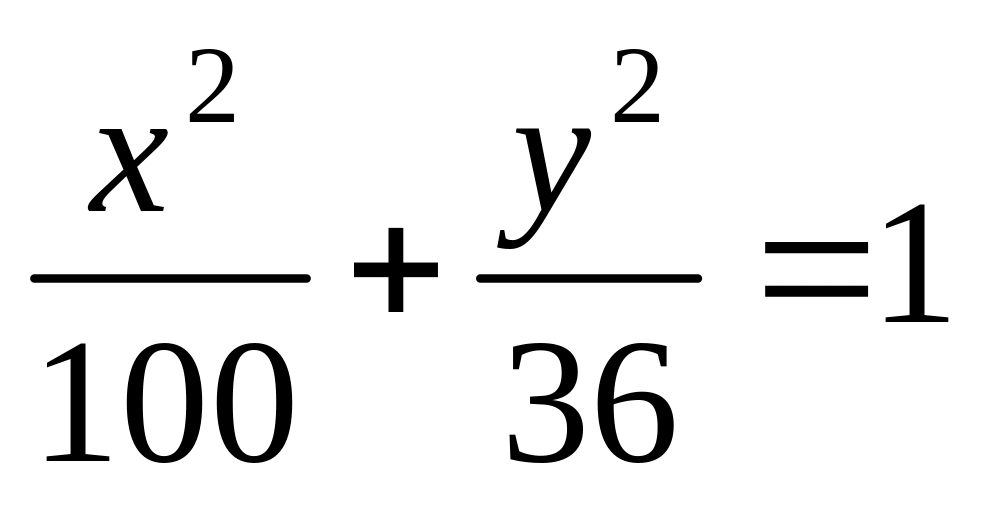знайти точку, відстань якої від правого
фокуса в чотири рази більша за відстань
від лівого фокуса.
Відповідь.
.
Еліпс проходить через точку
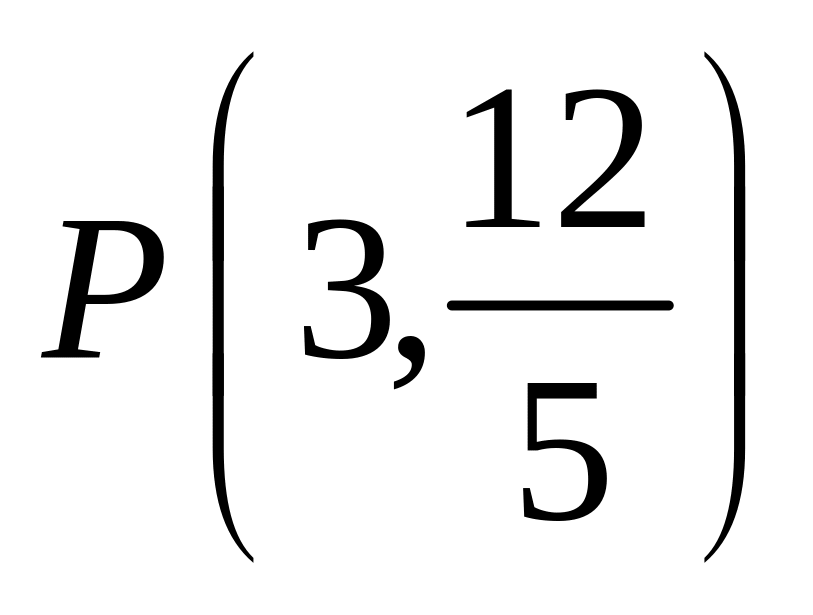і дотикається до прямої 4х
+ 5у
– 25 = 0. Записати рівняння цього еліпса
і знайти координати точки дотику.
Відповідь.
.
Знайти рівняння кола, описаного навколо трикутника з вершинами А(7; 7), В(0; 8), С(– 2; 4).
Відповідь.
Записати рівняння кола з центром у точці (6; 7), що дотикається до прямої
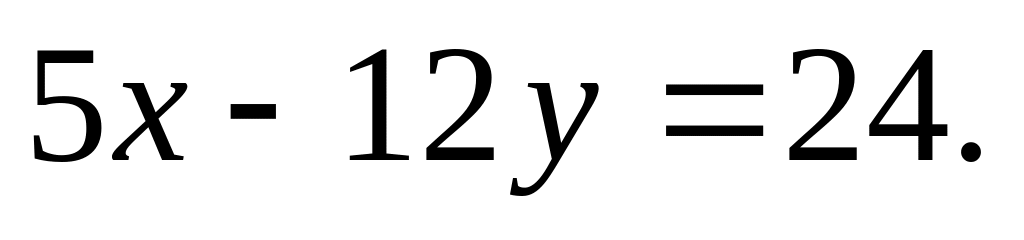
Відповідь.
В еліпс
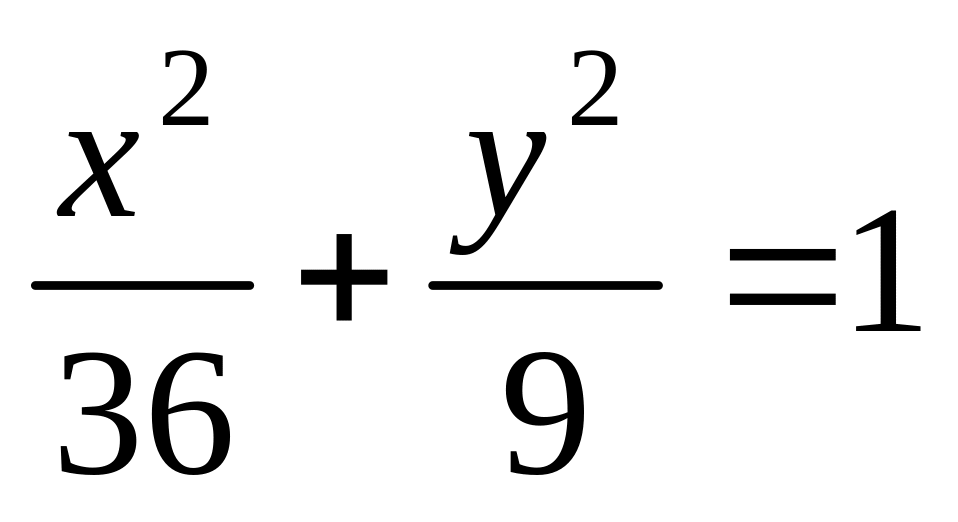вписано правильний трикутник так, що
одна з його вершин збігається з правим
кінцем великої осі. Знайти координати
двох інших вершин.
Відповідь.
.
Записати рівняння прямої, що дотикається до еліпса
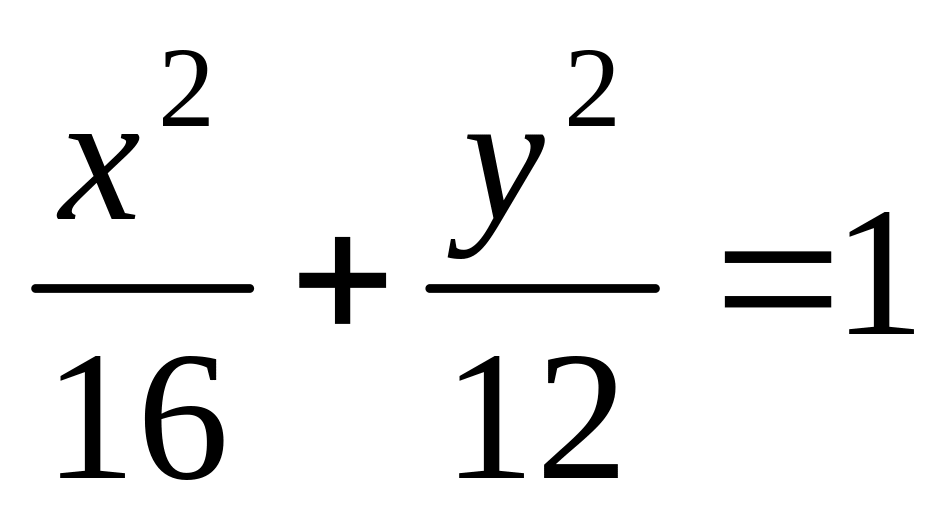у точці (2; – 3).
Відповідь.
Знайти рівняння тих дотичних до еліпса
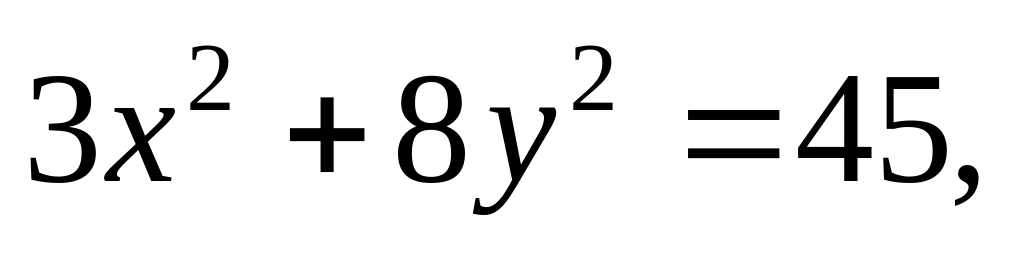відстань яких від центра еліпса дорівнює
3.
Відповідь.
Гіпербола дотикається до прямої
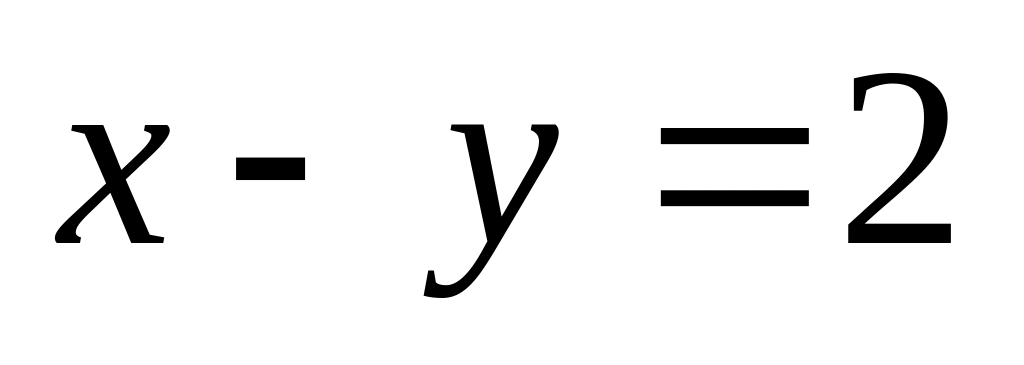у точці (4; 2). Скласти рівняння гіперболи.
Відповідь.
До параболи
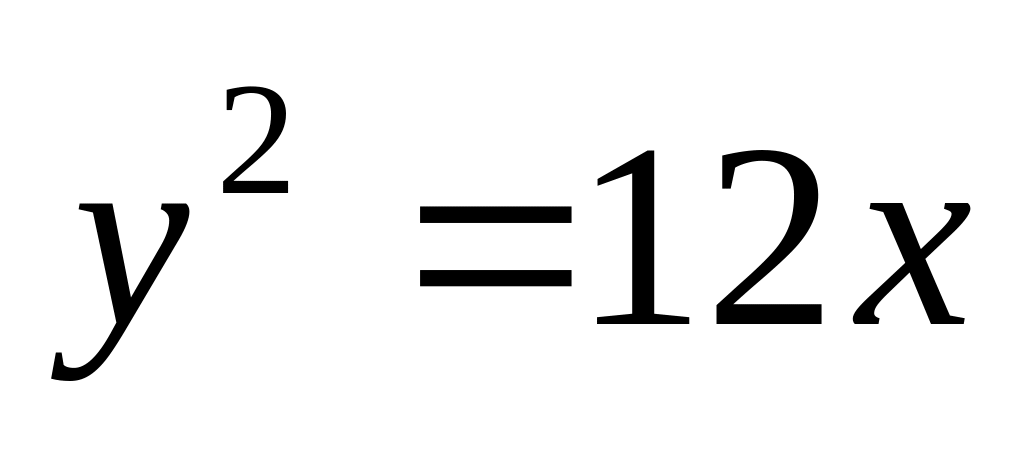провести дотичну паралельно прямій
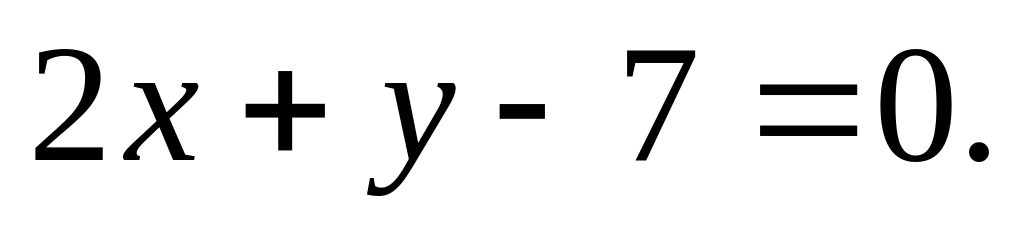
Відповідь.
Знайти кут між асимптотами гіперболи, в якої:
а)
ексцентриситет
б) відстань між фокусами вдвічі більша за відстань між директрисами.
Відповідь. а) 120; б) 90.
Записати рівняння прямої, що дотикається до гіперболи
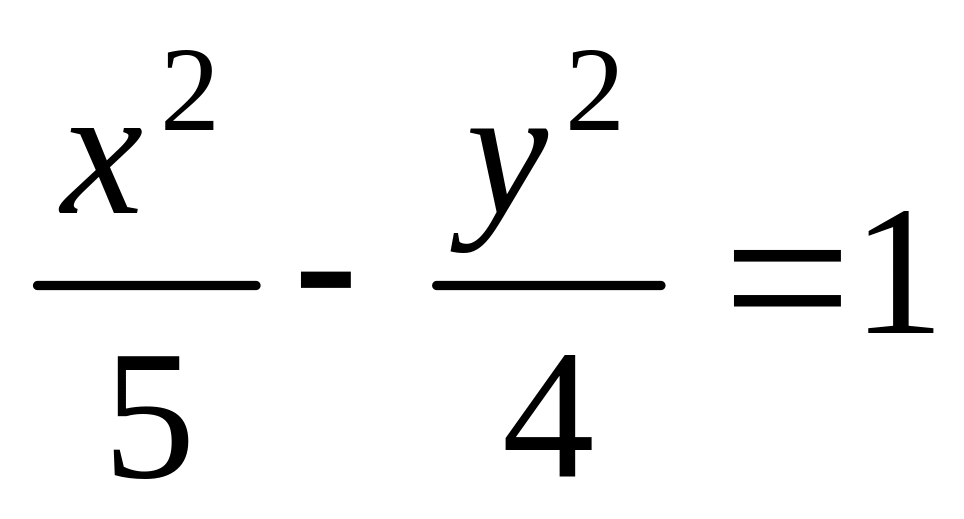у точці (5, – 4).
Відповідь. х + у =1.
Знайти найкоротшу відстань параболи
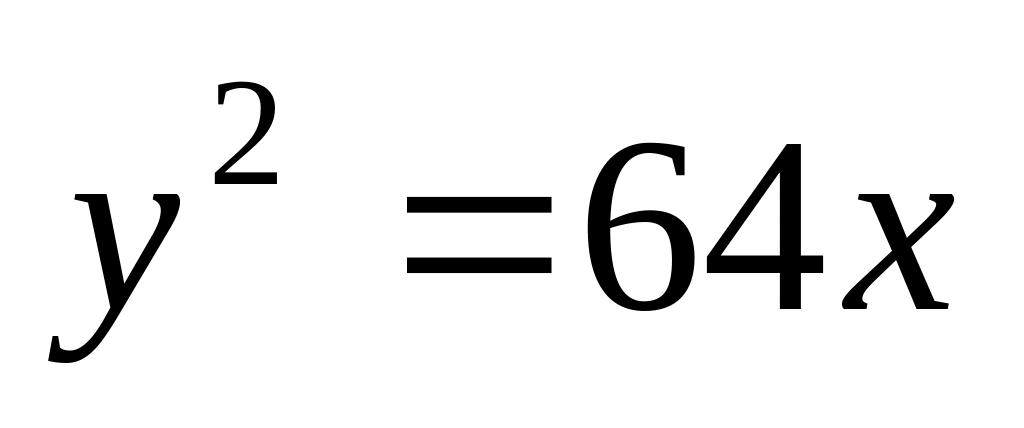до прямої
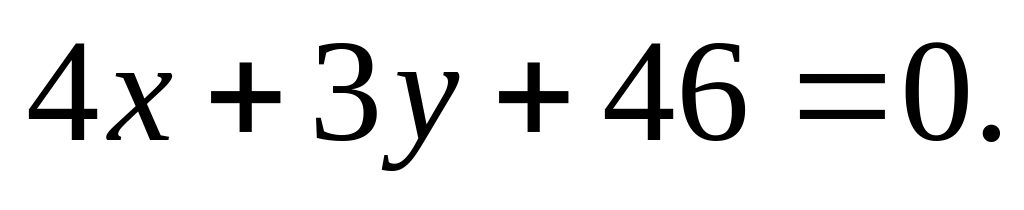
Відповідь. 2.
Визначити типи таких кривих:
а)
б)
в)
г)
д)
Відповідь. а) гіпербола; б) еліпс; в) пара прямих, що перетинаються; г) парабола; д) пара паралельних прямих.
Завдання для
самостійної роботи: № 3; 5; 8; 10.
Практичне заняття № 6
Похідна
План
1. Знаходження похідних функцій.
2. Рівняння дотичної та нормалі до плоскої кривої.
3. Похідна складної функції.
Термінологічний словник ключових понять
Похідна функція — це границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
Геометричний
зміст похідної
—
похідна
чисельно дорівнює кутовому
коефіцієнту дотичної, проведеної до
графіка функції
у точці з абсцисою х.
Навчальні завдання
Приклад. Який кут утворює з віссю Ох дотична до кривої
,
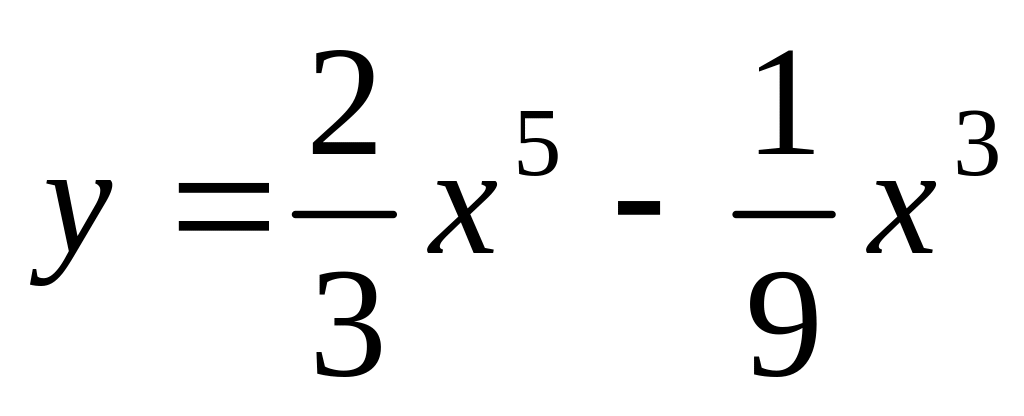проведена в точці з абсцисою х
= 1?
Знаходимо
похідну
;
при х
= 1,
,
таким чином
,
звідки
.
Застосовуючи формули та правила диференціювання, знайти похідні таких функцій:
2.
Приклад.
.
3.
Приклад.
.
.
4.
Приклад.
.
.
5.
Приклад.
.
6.
Приклад.
.
Логарифмуючи
функцію, дістаємо
.
Звідки:
,
,
.
7.
Приклад.
.
Маємо:
,
.
8.
Приклад.
Задано функцію
.
Знайти
Маємо:
,
,
.
Завдання для перевірки знань
Знайти похідні функцій:
1.
.
Відповідь.
.
2.
.
Відповідь.
.
3.
.
Відповідь.
4.
. Відповідь.
.
5.
.
Відповідь.
.
6.
.
Відповідь.
.
Застосовуючи формули та правила диференціювання, знайти похідні таких функцій:
7.
Відповідь.
.
8.
.
Відповідь.
.
9.
.
Відповідь.
.
10.
.
Відповідь.
.
11.
.
Відповідь.
.
12.
.
Відповідь.
.
13.
.
Відповідь.
.
14.
.
Відповідь.
.
15.
.
Відповідь.
.
16.
. Відповідь.
.
17.
. Відповідь.
.
18.
. Відповідь.
.
19.
. Відповідь.
.
20.
. Відповідь.
.
21.
. Відповідь.
.
22.
. Відповідь.
.
Знайти похідні другого порядку від функцій:
1.
. Відповідь.
.
2.
. Відповідь.
.
3.
. Відповідь.
.
4.
.
Відповідь.
.
5.
. Відповідь.
.
6.
. Відповідь.
.
7.
. Відповідь.
.
9.
. Відповідь.
.
Завдання для
самостійної роботи: № І (1-4); ІІ (1-3); ІІІ
(1-3).
Практичне заняття № 7
Знаходження інтегралів безпосередньо і заміною
План
1. Методи інтегрування невизначеного інтеграла.
2. Інтегрування раціональних функцій.
3. Інтегрування тригонометричних функцій.