
- •Невизначений інтеграл лекція 12. Поняття первісної та невизначеного інтеграла. Властивості невизначеного інтеграла. Таблиця основних формул інтегрування
- •12.1. Первісна функція і невизначений інтеграл
- •12.2. Властивості невизначеного інтеграла
- •14.7. Інтеграли з нескінченними межами (невласні інтеграли I роду)
- •14.8. Інтеграл від необмеженої функції (невласні інтеграли II роду)
- •Диференціальні рівняння
- •15.1. Диференціальні рівняння, основні визначення
- •15.2. Диференціальні рівняння першого порядку (загальні поняття)
- •15.3. Диференціальні рівняння із розділеними змінними
- •15.4. Диференціальні рівняння із змінними, які розділяються
- •Лекція 16. Однорідні рівняння, їх розв'язок.
- •16.1. Однорідні рівняння першого порядку
- •Лекція 17. Лінійні диференціальні рівняння першого порядку. Підстановка бернуллі. Метод варіації довільної сталої
- •17.1. Лінійні рівняння першого порядку. Підстановка Бернуллі
- •17.2. Метод Лагранжа (метод варіації довільної сталої) для розв'язку лінійних рівнянь першого порядку
- •Лекція 18. Диференціальні рівняння виших порядків. Рівняння, які допускають зниження порядку. Задача коші
- •18.1. Рівняння виду
- •18.3. Рівняння II порядку, що дозволяють зниження порядку
- •19.1. Лінійні однорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •19.2. Лінійні неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •Числові ряди лекція 21. Числовий ряд, основні означення.Необхідна умова збіжності. Дії з рядами. Ряди з додатними членами та їх властивості
- •21.1. Визначення числового ряду. Сума ряду
- •21.2. Властивості числових рядів із додатними членами
- •21.3. Необхідна ознака збіжності ряду
- •Лекція 22. Достатні ознаки збіжності: порівняльна, даламбера, радикальна. Інтегральна ознака коші
- •22.1. Ознака порівняння
- •Лекція 23. Знакозмінні ряди. Абсолютна і умовна збіжність. Ряди зі знакочергуванням. Ознака лейбніца. Властивості знакозбіжних рядів
- •23.1. Знакозмінні ряди. Теорема Лейбніца
- •23.2. Знакопереміжні ряди. Абсолютна й умовна збіжність
- •23.3. Властивості абсолютно й умовно збіжних рядів
- •Функціональні ряди лекція 24. Область збіжності функціонального ряду
- •24.1. Область збіжності функціонального ряду
- •Означення. Ряд
- •Для всіх значень х в області збіжності ряду має місце співвідношення , тому
- •Лекція 25. Степеневий ряд, його область та інтервал збіжності. Властивості степеневих рядів. Радіус збіжності степеневого ряду
- •25.1. Степеневий ряд, його область та інтервал збіжності. Радіус збіжності степеневого ряду
- •Невизначений інтеграл
- •Визначений інтеграл
Числові ряди лекція 21. Числовий ряд, основні означення.Необхідна умова збіжності. Дії з рядами. Ряди з додатними членами та їх властивості
21.1. Визначення числового ряду. Сума ряду
Означення.
Нехай дана нескінченна послідовність
чисел
![]() Вираз
Вираз
![]() (21.1)
називається числовим
рядом.
При цьому числа
називаються членами
ряду,
(21.1)
називається числовим
рядом.
При цьому числа
називаються членами
ряду,
![]() - загальний
член ряду.
- загальний
член ряду.
Означення. Сума скінченого числа n перших членів ряду називається n-ою частковою сумою ряду:
![]() .
.
Розглянемо
часткові суми
![]() ,
,
![]() ,
,
![]() ,…,
...
,…,
...
Означення.
Якщо існує кінцева границя
![]() ,
то її називають сумою
ряду
(21.1) і говорять, що ряд збігається. Якщо
,
то її називають сумою
ряду
(21.1) і говорять, що ряд збігається. Якщо
![]() не існує, то говорять, що ряд (21.1)
розбігається і суми не має.
не існує, то говорять, що ряд (21.1)
розбігається і суми не має.
Приклад. Розглянемо ряд
![]() (21.2)
(21.2)
Це
геометрична
прогресія
з першим членом а
і знаменником q
![]() .
.
Сума n
перших членів геометричної прогресії
дорівнює (при
![]() ):
):
![]()
![]()
Якщо
![]() ,
то ряд (21.2) має вигляд
,
то ряд (21.2) має вигляд
![]() У цьому випадку
У цьому випадку
![]() ,
,
![]() ,
ряд розбігається.
,
ряд розбігається.
Якщо
![]() ,
то ряд (21.2) має вигляд
,
то ряд (21.2) має вигляд
![]() У цьому випадку
У цьому випадку
![]() Отже,
Отже,
![]() границі не має - ряд розбігається.
границі не має - ряд розбігається.
Теорема.
Геометричний ряд збігається при
![]() і розбігається при
і розбігається при
![]() .
.
21.2. Властивості числових рядів із додатними членами
Теорема 1. Якщо до ряду (21.1) додати або відняти кінцеве число членів ряду, то отриманий ряд збігається або розбігається одночасно з рядом (21.1).
Теорема
2.
Сталий множник виноситься за знак суми
ряду:
![]() .
.
Теорема
3.
Два збіжні ряди можна почленно складати
і їх сума дорівнює:
![]() .
.
Теорема 4. Сума (різниця) збіжного ряду і розбіжного є розбіжний ряд.
21.3. Необхідна ознака збіжності ряду
Теорема. Якщо ряд збігається, то його n-й член прямує до нуля при необмеженому зростанні n.
Доказ.
Нехай ряд
![]() збігається, тобто має місце рівність
збігається, тобто має місце рівність
![]() ,
де S
- сума ряду; то тоді має місце також
рівність
,
де S
- сума ряду; то тоді має місце також
рівність
![]() ,
тому що при
,
тому що при
![]() і
і
![]() .
Віднімаючи почленно з першої рівності
другу, получимо
.
Віднімаючи почленно з першої рівності
другу, получимо
![]() або
або
![]() .
.
Але
![]() .
.
Отже,
![]() ,
що і було потрібно довести.
,
що і було потрібно довести.
Зауваження.
Якщо
,
то ряд може бути збіжним і розбіжним, а
якщо
![]() ,
то ряд розбіжний.
,
то ряд розбіжний.
Приклад.
Ряд
![]() розбіжний, тому що
розбіжний, тому що
![]() .
.
Приклад.
Розглянемо ряд
![]() , який називається гармонічним.
, який називається гармонічним.
Тут
![]() ,
але проте ряд розбігається. Справді,
зараз ми доведемо, що
,
але проте ряд розбігається. Справді,
зараз ми доведемо, що
![]() при
.
при
.
Для доведення замінимо деякі члени ряду меншими числами і переконаємося, що навіть сума менших доданків буде прагнути до нескінченності. Випишемо декілька перших членів гармонічного ряду, розбивши їх на групи таким чином:
![]()
У кожній із круглих дужок замінимо усі доданки останнім, який залишимо без зміни. Одержимо (під кожній дужкою підписане число доданків у ній)
 Цілком
очевидно, що від такої заміни сума членів
у кожній дужці зменшилася і стала рівною
Цілком
очевидно, що від такої заміни сума членів
у кожній дужці зменшилася і стала рівною
![]() .
Оскільки таких дужок можна брати скільки
завгодно, сума їх буде прагнути до
нескінченності.
.
Оскільки таких дужок можна брати скільки
завгодно, сума їх буде прагнути до
нескінченності.
Із сказаного ясно, що часткові суми гармонічного ряду будуть нескінченно зростати, отже, ряд розбігається.
Лекція 22. Достатні ознаки збіжності: порівняльна, даламбера, радикальна. Інтегральна ознака коші
22.1. Ознака порівняння
Ознака
порівняння.
Нехай дані два ряди з невід'ємними
членами
![]() (22.1)
і
(22.1)
і
![]() (22.2) і нехай кожний член ряду (22.1) не
більше відповідного члена ряду (22.2),
тобто
(22.2) і нехай кожний член ряду (22.1) не
більше відповідного члена ряду (22.2),
тобто
![]()
![]() .
Тоді:
.
Тоді:
1) Якщо збігається ряд (22.2), то збігається і ряд (22.1).
2) Якщо розбігається ряд (22.1), то розбігається і ряд (22.2).
Для порівняння часто використовують ряди:
![]() ,
- збігається (геометрична прогресія)
,
- збігається (геометрична прогресія)
![]()
Приклад.
Дослідити на збіжність ряд
![]()
Розв'язок.
Члени даного ряду менше відповідних
членів ряду
![]() .
.
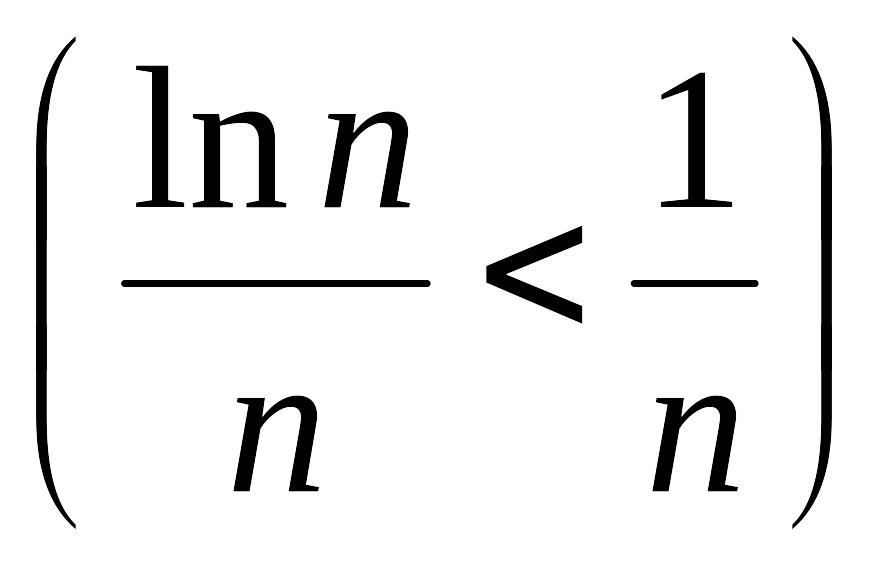 .
Так як ряд
,
складений із менших членів розбігається,
то і вихідний ряд теж розбігається.
.
Так як ряд
,
складений із менших членів розбігається,
то і вихідний ряд теж розбігається.
Приклад. Дослідити на збіжність ряд
![]()
Розв'язок.
Порівняємо даний ряд із рядом
![]() .
Тому що
.
Тому що
![]() і ряд
збігається як нескінченно спадаюча
геометрична прогресія, то і даний ряд
теж збігається.
і ряд
збігається як нескінченно спадаюча
геометрична прогресія, то і даний ряд
теж збігається.
22.2. Гранична форма ознаки порівняння
Гранична
форма ознаки порівняння.
Якщо
і
-
ряди з невід'ємними членами й існує
кінцевий, відмінний від нуля
![]() ,
то розглянуті ряди одночасно збігаються
або розбігаються.
,
то розглянуті ряди одночасно збігаються
або розбігаються.
Приклад.
Дослідити на збіжність ряд
![]() .
.
Розв'язок. Порівняємо ряд із гармонічним рядом .
![]() .
.
Отже, даний ряд розбігається.
22.3. Ознака Даламбера
Ознака
Даламбера.
Нехай маємо ряд із додатними членами
.
Якщо існує
![]() ,
то при
,
то при
![]() ряд збігається, при
ряд збігається, при
![]() ряд розбігається, при
потрібні додаткові дослідження - ознака
відповіді не дає.
ряд розбігається, при
потрібні додаткові дослідження - ознака
відповіді не дає.
Приклад.
Дослідити на збіжність ряд
![]() .
.
Розв'язок.
Скористаємося ознакою Даламбера; маємо
![]() ,
,
![]() ;
виходить,
;
виходить,
![]() .
.
Даний ряд збігається.
22.4. Радикальна ознака Коші
Радикальна
ознака Коші.
Якщо для ряду з невід'ємними членами
існує
![]() ,
то при
ряд збігається, при
ряд розбігається, при
потрібні додаткові дослідження - ознака
відповіді не дає.
,
то при
ряд збігається, при
ряд розбігається, при
потрібні додаткові дослідження - ознака
відповіді не дає.
Приклад.
Дослідити на збіжність ряд
![]() .
.
Розв'язок.
Тут зручно застосувати ознаку Коші,
оскільки
![]() ,
а границя останнього дробу знаходиться
просто:
,
а границя останнього дробу знаходиться
просто:
![]() .
.
Даний ряд збігається.
22.5. Інтегральна ознака Коші
Інтегральна ознака Коші. Нехай дано ряд із невід'ємними членами, члени якого є значеннями неперервної функції при цілих значеннях аргументу х:
![]() і
нехай
монотонно спадає на інтервалі
і
нехай
монотонно спадає на інтервалі
![]() .
Тоді ряд збігається, якщо збігається
невласний інтеграл
.
Тоді ряд збігається, якщо збігається
невласний інтеграл
![]() ,
і розбігається, якщо цей інтеграл
розбігається.
,
і розбігається, якщо цей інтеграл
розбігається.
Приклад.
Дослідити на збіжність ряд
![]() .
.
Розв'язок.
Скористуємося інтегральною ознакою
Коші:
![]() ; отже,
; отже,
![]() .
.
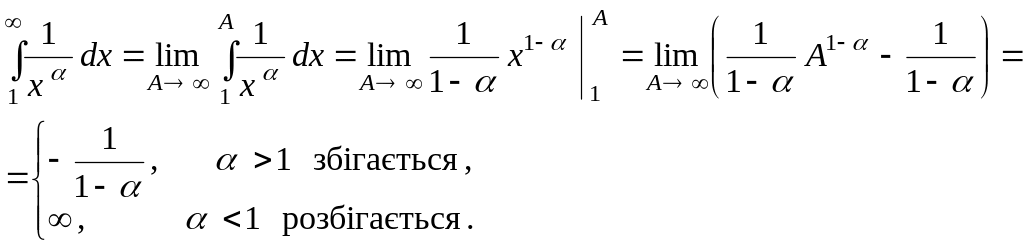 При
:
При
:
![]() .
Ряд розбігається.
.
Ряд розбігається.
