
- •Невизначений інтеграл лекція 12. Поняття первісної та невизначеного інтеграла. Властивості невизначеного інтеграла. Таблиця основних формул інтегрування
- •12.1. Первісна функція і невизначений інтеграл
- •12.2. Властивості невизначеного інтеграла
- •14.7. Інтеграли з нескінченними межами (невласні інтеграли I роду)
- •14.8. Інтеграл від необмеженої функції (невласні інтеграли II роду)
- •Диференціальні рівняння
- •15.1. Диференціальні рівняння, основні визначення
- •15.2. Диференціальні рівняння першого порядку (загальні поняття)
- •15.3. Диференціальні рівняння із розділеними змінними
- •15.4. Диференціальні рівняння із змінними, які розділяються
- •Лекція 16. Однорідні рівняння, їх розв'язок.
- •16.1. Однорідні рівняння першого порядку
- •Лекція 17. Лінійні диференціальні рівняння першого порядку. Підстановка бернуллі. Метод варіації довільної сталої
- •17.1. Лінійні рівняння першого порядку. Підстановка Бернуллі
- •17.2. Метод Лагранжа (метод варіації довільної сталої) для розв'язку лінійних рівнянь першого порядку
- •Лекція 18. Диференціальні рівняння виших порядків. Рівняння, які допускають зниження порядку. Задача коші
- •18.1. Рівняння виду
- •18.3. Рівняння II порядку, що дозволяють зниження порядку
- •19.1. Лінійні однорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •19.2. Лінійні неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •Числові ряди лекція 21. Числовий ряд, основні означення.Необхідна умова збіжності. Дії з рядами. Ряди з додатними членами та їх властивості
- •21.1. Визначення числового ряду. Сума ряду
- •21.2. Властивості числових рядів із додатними членами
- •21.3. Необхідна ознака збіжності ряду
- •Лекція 22. Достатні ознаки збіжності: порівняльна, даламбера, радикальна. Інтегральна ознака коші
- •22.1. Ознака порівняння
- •Лекція 23. Знакозмінні ряди. Абсолютна і умовна збіжність. Ряди зі знакочергуванням. Ознака лейбніца. Властивості знакозбіжних рядів
- •23.1. Знакозмінні ряди. Теорема Лейбніца
- •23.2. Знакопереміжні ряди. Абсолютна й умовна збіжність
- •23.3. Властивості абсолютно й умовно збіжних рядів
- •Функціональні ряди лекція 24. Область збіжності функціонального ряду
- •24.1. Область збіжності функціонального ряду
- •Означення. Ряд
- •Для всіх значень х в області збіжності ряду має місце співвідношення , тому
- •Лекція 25. Степеневий ряд, його область та інтервал збіжності. Властивості степеневих рядів. Радіус збіжності степеневого ряду
- •25.1. Степеневий ряд, його область та інтервал збіжності. Радіус збіжності степеневого ряду
- •Невизначений інтеграл
- •Визначений інтеграл
Невизначений інтеграл лекція 12. Поняття первісної та невизначеного інтеграла. Властивості невизначеного інтеграла. Таблиця основних формул інтегрування
12.1. Первісна функція і невизначений інтеграл
Займаючись диференціюванням функцій, ми ставили перед собою таку задачу: по даній функції знайти її похідну. Тепер перейдемо до вивчення оберненої задачі: знайти функцію, знаючи її похідну.
Означення.
Функція
![]() називається первісною
для функції
називається первісною
для функції
![]() для
для
![]() ,
якщо у всіх точках
,
якщо у всіх точках
![]() виконується рівність
виконується рівність
![]() .
.
Якщо
функція
має первісну
,
то вона має нескінченну множину первісних,
причому всі первісні знаходяться у
виразі
![]() ,
де С - деяке дійсне число.
,
де С - деяке дійсне число.
Означення.
Невизначеним
інтегралом
від функції
називається множина всіх її первісних
і позначається символом
![]() .
Таким чином, за означенням,
.
Таким чином, за означенням,
![]() ,
якщо
.
При цьому функцію
називають підінтегральною
функцією,
,
якщо
.
При цьому функцію
називають підінтегральною
функцією,
![]() - підінтегральним
виразом,
знак
- підінтегральним
виразом,
знак
![]() -
знаком
інтеграла.
-
знаком
інтеграла.
Знаходження невизначеного інтеграла називається інтегруванням функції.
12.2. Властивості невизначеного інтеграла
1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції, тобто, якщо , то і
![]() .
.
2. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу
![]() .
.
3. Невизначений інтеграл від диференціала деякої функції дорівнює цієї функції плюс довільна стала
![]() .
.
4. Невизначений інтеграл від алгебраїчної суми двох або декількох функцій дорівнює алгебраїчній сумі інтегралів:
![]() .
.
5.
Постійний множник можна виносити за
знак інтеграла, тобто, якщо
![]() ,
то
,
то
![]() .
.
6. Якщо , то
![]() .
.
12.2. Таблиця інтегралів
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ЛЕКЦІЯ 13. МЕТОДИ ІНТЕГРУВАННЯ
13.1. Безпосереднє інтегрування
Безпосереднім інтегруванням будемо називати інтегрування за допомогою властивостей невизначеного інтеграла, тотожних перетворень підінтегральної функції і таблиці основних інтегралів.
Приклад.
![]() .
.
Приклад.
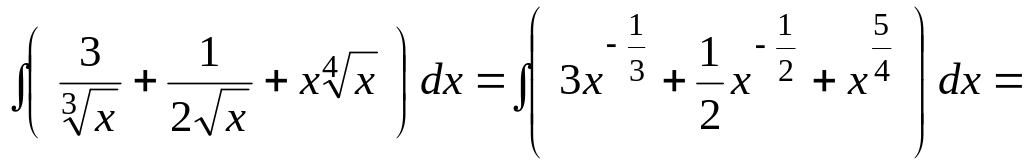
![]() .
.
Приклад.
Використавши властивість № 6 знайти
![]() .
.
Приклад.
![]() .
.
Приклад.
![]() .
.
13.2. Інтегрування методом заміни змінної
Заміна змінної в невизначеному інтегралі проводиться за допомогою підстановок двох видів:
1)
![]() ,
де
,
де
![]() - монотонна, неперервно диференційовна
функція нової змінної t.
Тоді
- монотонна, неперервно диференційовна
функція нової змінної t.
Тоді
![]() .
Формула заміни змінної в цьому випадку
має вид
.
Формула заміни змінної в цьому випадку
має вид
![]() .
.
2)
![]() ,
де t
- нова змінна. Формула заміни змінної
при такій підстановці має вид
,
де t
- нова змінна. Формула заміни змінної
при такій підстановці має вид
![]() .
.
Приклад.
![]()
Приклад.
![]() .
.
Приклад.
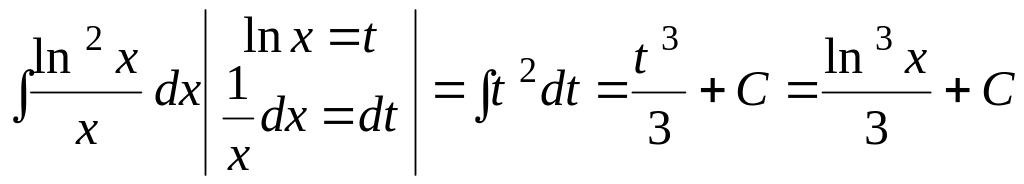 .
.
Приклад.
![]() .
.
13.3. Метод інтегрування частинами
Нехай
![]() і
і
![]() -
дві неперервно диференційовані функції
від х.
Тоді використавши формулу для диференціала
добутку
-
дві неперервно диференційовані функції
від х.
Тоді використавши формулу для диференціала
добутку
![]() :
:
![]() .
.
Маємо
![]() або
або
![]() .
(1)
.
(1)
Ця
формула називається формулою
інтегрування частинами.
За допомогою цієї формули знаходження
інтеграла
![]() зводиться до знаходження іншого інтеграла
зводиться до знаходження іншого інтеграла
![]() ;
її застосування доцільно в тих випадках,
коли останній інтеграл або простіше
вихідного, або йому подібний.
;
її застосування доцільно в тих випадках,
коли останній інтеграл або простіше
вихідного, або йому подібний.
При цьому за u береться така функція, яка при диференціюванні спрощується, а за dv - та частина підінтегрального виразу, інтеграл від якої відомий або може бути знайдений.
Класи
інтегралів, що інтегруються частинами:
![]() ,
,
![]() ,
,
![]() ,
де
,
де
![]() - многочлен, за u
слід прийняти
,
а за dv
- відповідно вирази
- многочлен, за u
слід прийняти
,
а за dv
- відповідно вирази
![]() ,
,
![]() ,
,
![]() ;
для інтегралів виду
;
для інтегралів виду
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() за u
приймаються відповідно функції
за u
приймаються відповідно функції
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() , а за dv
- вираз
, а за dv
- вираз
![]() .
.
Приклад.
![]()
![]() .
.
Приклад.
![]()
![]() .
.
Приклад.
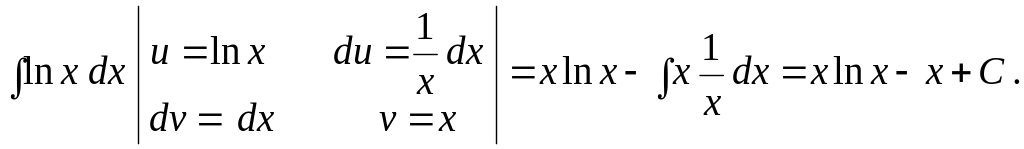
Приклад.
![]()
Проінтегрувавши частинами ще раз маємо
![]()
Після двократного інтегрування частинами, ми в правій частині знову одержали початковий інтеграл. Таким чином, приходимо до рівняння з невідомим інтегралом. З цього рівняння знаходимо
![]() тобто
тобто
![]()
ВИЗНАЧЕНИЙ ІНТЕГРАЛ
14.2. Формула Ньютона - Лейбніца
![]() ,
(2)
,
(2)
де
![]() -
первісна функції
-
первісна функції
![]() або невизначений інтеграл.
або невизначений інтеграл.
Приклад. Обчислити визначений інтеграл:
![]() .
.
14.3. Властивості визначеного інтеграла
Визначений інтеграл має ті ж властивості, що й невизначений. Крім того:
1о.
Якщо відрізок інтегрування [a,
b]
розбитий на дві частини [a,
с]
і [с,
b],
то
![]() .
.
2о.
![]() .
.
3о.
![]() ,
якщо
,
якщо
![]() .
.
4о.
![]() ,
якщо
,
якщо
![]() .
.
14.4. Заміна змінної у визначеному інтегралі
Має місце наступна формула заміни змінної у визначеному інтегралі
![]() ,
,
![]() ,
,
![]() .
.
Приклад. Обчислити визначені інтеграли:
а)
![]()
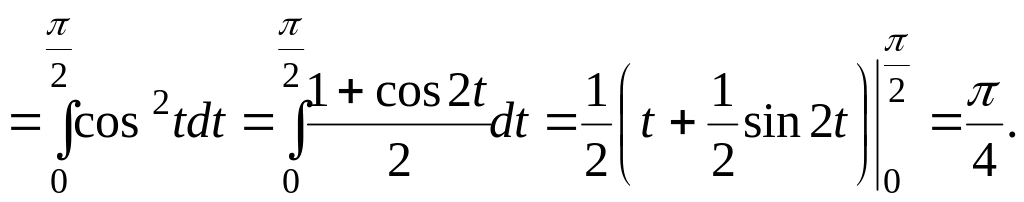
б)
![]()
![]()
14.5. Інтегрування частинами у визначеному інтегралі
Застосувавши формулу Ньютона-Лейбница до формули інтегрування частинами, маємо
![]()
![]() (3)
(3)
Приклад. Обчислити визначений інтеграл:
![]()
14.6. Обчислення площ плоских фігур за допомогою визначеного інтеграла
 Якщо
на [a,
b]
функції
Якщо
на [a,
b]
функції
![]() і
і
![]() неперервні, то площа області, обмеженої
знизу графіком функції
,
зверху - графіком функції
,
зліва - прямою
неперервні, то площа області, обмеженої
знизу графіком функції
,
зверху - графіком функції
,
зліва - прямою
![]() ,
справа - прямою
,
справа - прямою
![]() обчислюється за формулою:
обчислюється за формулою:
![]()
Я кщо
на [a,
b]
функції
кщо
на [a,
b]
функції
![]() і
і
![]() неперервні, то площа області, обмеженої
зліва графіком функції
,
справа - графіком функції
,
знизу - прямою
неперервні, то площа області, обмеженої
зліва графіком функції
,
справа - графіком функції
,
знизу - прямою
![]() ,
зверху - прямою
,
зверху - прямою
![]() обчислюється за формулою:
обчислюється за формулою:
![]()
П риклад.
Обчислити площу області, обмеженої
лініями
риклад.
Обчислити площу області, обмеженої
лініями
![]() ,
,
![]() ,
,
![]() .
.
Розв'язок.
![]() (кв.
од.)
(кв.
од.)

Приклад.
Обчислити площу області, обмеженої
лініями
![]() ,
,
![]() ,
віссю ординат і прямою
,
віссю ординат і прямою
![]() .
.
Розв'язок.![]()
![]()
