3.3.2 Второй и третий квадранты.
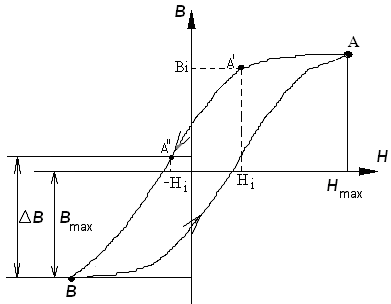
по формуле
,
где 
модуль
значения напряженности в исследуемой
точке;
замыкаем К, П – в положение 1. Магнитное состояние – т.А;
выбираем предел измерения , устанавливая
,
равное
.
Размыкаем К;изменяя , устанавливаем ток . Магнитное состояние образца - т. ;
замыкаем К, тогда магнитное состояние – т.А;
магнитная подготовка: оставляем П в положении 1;
размыкаем К. Магнитное состояние - т. ;
не включая интегратор (И), размыкаем К. Магнитное состояние - т.
;включаем интегратор (И) и размыкаем К. Магнитное состояние – т.В. Интегратор покажет значение, пропорциональное В:
.
3.4 Погрешности определения основной кривой намагничивания.
(Погрешности определения параметров динамического цикла определяются аналогично)
Уравнение измерения:
;
где 
.
По заданному (с погрешностью) току мы определим величины (тоже с погрешностью):
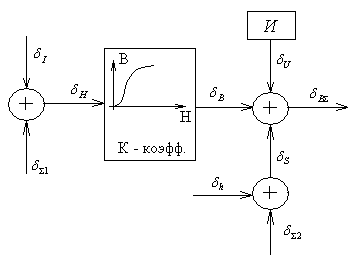
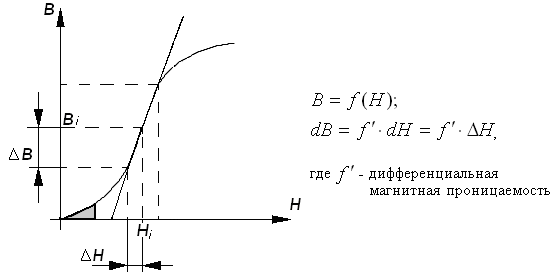
На рисунке обозначено:
относительная погрешность установки
тока
,
определяется классом точности амперметра;
относительная погрешность определения
суммы
,
определяется погрешностью изменения
и
;
относительная погрешность установки
заданной напряженности;
относительная погрешность измерения
потока интегратором (И);
относительная погрешность площади
сечения образца;
относительная погрешность определения
В;
относительная погрешность измерения
толщины образца;
относительная погрешность разности
суммарная погрешность измерения
индукции.
Выясним, каким образом
трансформируется в
.
1) Сделаем это качественным методом:
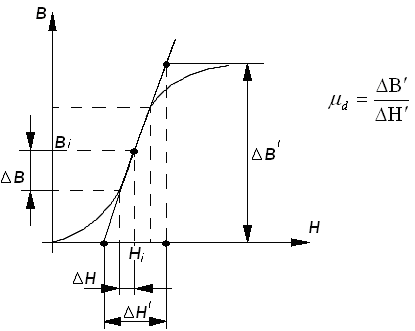
Из рисунка видно, что
можно определить по динамической
проницаемости.
Общее выражение для относительной погрешности измерения индукции:
;
.
Чтоб вычислить относительную погрешность, разделим правую и левую части на В:
.
Правую часть умножим и разделим на Н:
.
Запишем уравнение погрешности при следующих условиях поведения объекта:
1) ток
устанавливается амперметром с классом
точности
.
Тогда относительная погрешность :
,
где 
предел измерения амперметра;
то значение тока, которое мы устанавливаем.
2) диаметры
,
и
измеряются с одинаковой абсолютной
погрешностью
.
Тогда:
,
где 
средний диаметр образца.
;
.
3) для измерения использован прибор Ф5050. Воспользовавшись данными его технических характеристик, запишем:
,
где 
предел измерения прибора;
результат измерения.
Исходя и полученных выше уравнений, запишем:
.
3.5 Приборы, применяющиеся при измерении индукции импульсно-индукционным методом измерения.
При импульсно-индукционном методе измерений ЭДС которая индуцируется в измерительной обмотке по модулю равна следующему выражению:
.
Для того чтобы определить индукцию необходимо вычислить интеграл:
,
где 
время изменения напряженности;
изменение потокосцепления.
Таким образом, приборы, которые используются при импульсно-индукционном методе измерения, должны быть интеграторами.
Используются такие приборы:
цифровые интеграторы;
баллистические гальванометры;
магнитоэлектрические веберметры и т.д.