2 Величины, описывающие поведение магнитных материалов в магнитном поле.

2.1 Намагничиваемость вещества.

Мысленно сделаем следующий опыт: предположим, что имеется соленоид, по которому протекает ток . Количество витков соленоида = . Контур интегрирования ( ) проходит внутри соленоида.

Для циркуляции:

Эта формула показывает, что единственной причиной поля является ток.

В этот соленоид поместим магнитный материал:

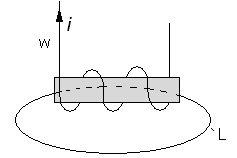
Опыт показывает, что магнитное поле в каждой точке контура усиливается, следовательно, индукция в каждой точке увеличится.

Если учитывать, что индукция обусловлена потоком, то в правую часть уравнения для второго рисунка при возросшей индукции необходимо добавить слагаемое, которое имеет структуру . Пока назовем элементарным током.

Таким образом, для второго рисунка можно написать формулу:

Назовем - внешние потоки.

Элементарные токи создаются вращающимися электронами, орбиты которых пронизываются контуром интегрирования, а также движущимися зарядами внутри ядра, если контур интегрирования проходит через ядро.

Попробуем ответить на вопрос: создаются ли токи всем объемом вещества, или только частью его?

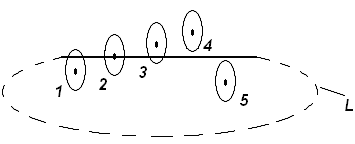
Учитывая рис.2, можно сделать вывод, что а атомы 4, 5 не создают циркуляцию, а 1, 2, 3 – создают.

Следовательно, циркуляцию создает «столбик» вещества, который имеет форму цилиндра, диаметр которого равен удвоенному диаметру орбиты

электрона, а длина – длине образца.

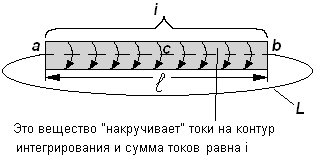
рис.3

Попробуем ответить на вопрос: как сравнить материалы по способности увеличивать поле?

Для того чтоб сравнить материалы, имеющие разную длину по способности «накручивать» токи на контур интегрирования разделим токи на длину образца. Этой величиной можно пользоваться, если она одинакова во всех точках вещества. Если это условие не выполняется, переходим к характеристике в каждой точке: ,

где бесконечно малое приращение тока;

бесконечно малая длина.

Эта величина называется намагниченностью вещества, вернее его модуль.

Модуль намагничиваемости вещества ( ) направлен так же как и индукция и определяется по формуле:

Физический смысл : это ток, накручиваемый на контур интегрирования длиной 1 метр.

Модуль для хороших материалов может достигать .

2.2 Напряженность магнитного поля.

Вернемся к уравнению .

Для рис.3: - поскольку токи распространяются только по длине acb мы можем распространить по всему контуру.

С учетом последнего уравнения запишем: .

Разделим обе части на : .

Объединим интегралы в правой и левой части: .

По определению величина равна напряженности магнитного поля: .

Напряженность и модуль намагничиваемости имеют одинаковые единицы измерения ( ). Если нет магнитного вещества, то и мы получаем уравнение, которое не противоречит напряженности в вакууме: .

Напряженность создается внешним воздействием (током ) и не зависит от свойств материала.

При магнитных измерениях стараются выбрать такой метод, чтобы было одинаковым по всему контуру интегрирования.

1.

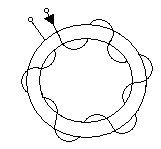
На кольцевую форму образца равномерно наносится обмотка.

2. Если длина катушки достаточно превышает ее диаметр, то есть точные формулы расчета напряженности.

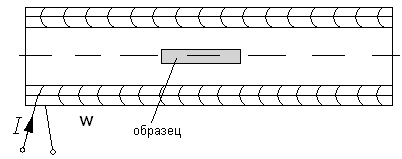
Эта схема позволяет исследовать не замкнутые пластины.

3. Кольцо Гельмгольца.

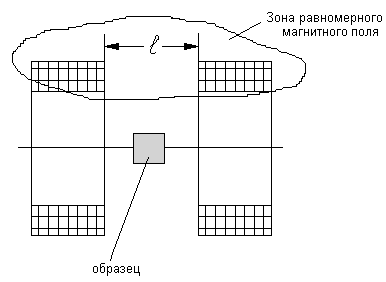
Преимуществом, по сравнению с предыдущим вариантом, является то, что посередине есть пространство, в которое свободно можно внести образец (тело).

Если постоянно ( ) то напряженность не всегда следует измерять, ее можно задать, установить с помощью амперметра и коэффициента, зависящего от геометрических размеров образца т.е. коэффициента пропорциональности :

.

Выводы:

1. Три вектора: индукция , напряженность и намагниченность полностью определяют поведение материала в магнитном поле.

Вектор определяет вектор индукции , который создается самим веществом.

Вектор определяет часть вектора ( ), которая создается внешними токами (токам намагничивания).

Вектор характеризует суммарное магнитное поле в веществе, создаваемое как внешним, так и внутренним воздействием.

2. Размерность и отличается от размерности , но мы можем всегда привести их к одной размерности: .