1.2 Циркуляция вектора магнитной индукции

, где L – замкнутый контур

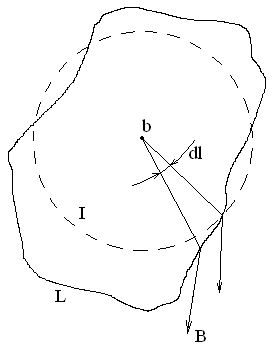
Попробуем вычислить циркуляцию для простейшего случая.

Имеется проводник с током, который протекает перпендикулярно плоскости доски. Выберем любой замкнутый контур L, который расположен в плоскости доски. Для вычисления выберем участок dl, индукция в этой точке будет направлена по касательной.

Предположим

1)

- в данной формуле 1 виток, если витков много, то умножим на их количество.

Рассмотрим частный случай:

2) в каждой точке этого контура

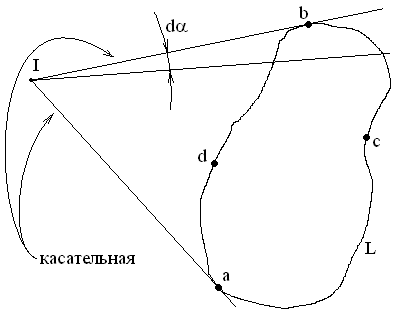
Начинаем обход с точки b по контуру => … один раз , второй раз => . Этот интеграл равен

Циркуляция отлична от нуля только в том случае, если ток пронизывает контур интегрирования L. Если этот контур не пронизывают токи, то циркуляция равна нулю. Таким образом циркуляцию можно рассматривать как меру

тока, которая пронизывает контур.

Рассмотрим частный случай:

3) предположим контур интегрирования такой:

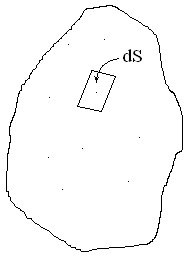
где –плотность тока

I –суммарный ток через этот контур

S –площадь, ограниченная замкнутым контуром L.

В левой части уравнения интеграл по контуру, а в правой части интеграл по площади, охваченной этим контуром.

1.3 Ротор вектора индукции

1)

В этом случае циркуляция:

2)

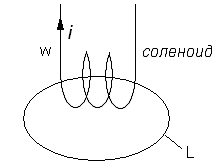
Контур интегрирования проходит внутри соленоида.

3)

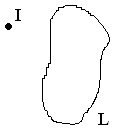рис. 1

Предположим, что ток проходит перпендикулярно рисунку и контур интегрирования не пронизывается током.

1.3 Напряженность магнитного поля в вакууме

Возьмем уравнение и разделим на :

По определению, величину назовем напряженностью магнитного поля в вакууме – H.

В результате:

Вектор H имеет такое же направление, как и вектор B и отличается от B на какой-то коэффициент. Следовательно, нет смысла вводить еще один вектор напряженности (во всяком случае, для вакуума).

Предположим, есть вектор плотности тока, который перпендикулярен каждой точке плоскости рисунка:

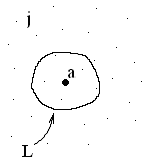
рис.2

j – плотность тока

Выбираем точку A и окружаем ее контуром L. Контур L ограничивает (охватывает) площадь S. Вычислим циркуляцию вектора B по контуру L:

- циркуляция.

Можно сказать, что эту циркуляцию генерирует контур L со своей площадью. Естественно эта циркуляция зависит от площади.

(Нам хотелось бы создать такую величину, которая бы характеризовала циркуляцию вектора.)

Чтобы оценить способность генерировать циркуляцию в точке A будем стягивать контур L к точке A так, чтобы она (точка A) все время оставалась внутри контура. При этом будем вычислять интеграл:

(*)

Если , то эту величину (*) называют модулем ротора индукции B.

Ротор направлен так, что обход по контуру, если смотреть из острия этого вектора, происходит в положительном направлении.

Вывод: как и любое векторное поле, вектор магнитной индукции порождает две величины:

1. скалярная величина ;

2. векторная величина ;

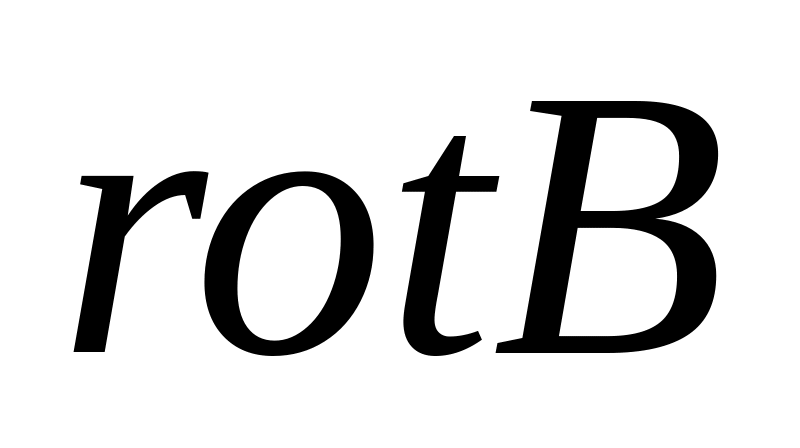Только для вектора магнитной индукции . Такое поле называется вихревым или соленоидным.

Формула Стокса.

Позволяет заменить интеграл по контуру интегралом по площади (или наоборот):

.

Взаимосвязь ротора вектора индукции с вектором плотности тока:

(Вернемся к рисунку 2). Ток, пронизывающий площадь , можно вычислить по формуле:

(при условии перпендикулярности к доске вектора . При условии другого угла ( ) формула принимает вид: ). Следовательно, плотность тока – скаляр, ток – вектор.

Учтем формулу

.

Тогда

.

В этом уравнении слева – интеграл по контуру, справа – интеграл по площади.

Применим формулу Стокса:

- интеграл по одной переменной.

Перепишем это уравнение следующим образом:

Мы получили одно из основных уравнений Максвелла:

.

Вывод: для вектора магнитной индукции дивергенция = 0, а ротор = .