1.1.3 Формула Остроградского

,

где замкнутая поверхность;

объем, который заключен в замкнутой поверхности.

Формула позволяет заменить интеграл по поверхности интегралом по объему.

Как мы знаем: .

Следовательно .

Последнее уравнение – это еще одна запись принципа непрерывности магнитного поля.

1.1.4 Основные уравнения, связывающие электрические и магнитные величины.

Среди основных величин в системе СИ есть одна величина – сила электрического тока, которая позволяет установить вместе с другими единицами единицы измерения электрических и магнитных величин.

Формула Ампера.

Она используется для установления силы электрического тока:

где токи, протекающие по двум проводникам бесконечной длины и бесконечно малого сечения, расположенные на расстоянии b друг от друга;

сила взаимодействия на расстоянии 1м;

магнитная постоянная, одна из фундаментальных постоянных электромагнитного поля.

Для установления магнитной постоянной примем:

тогда:

- это коэффициент, определяемый выбором системы единиц.

Поле движущегося заряда.

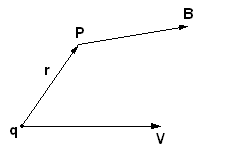
Сконструируем формулу для вычисления индукции , будем при этом учитывать:

1. Эта формула содержит .

2. Индукция – величина векторная, зависящая от векторов 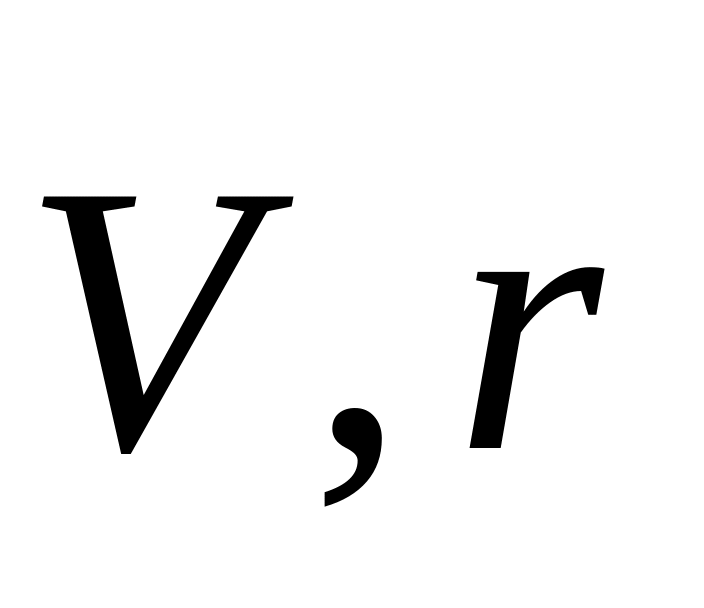, следовательно, формула содержит множитель .

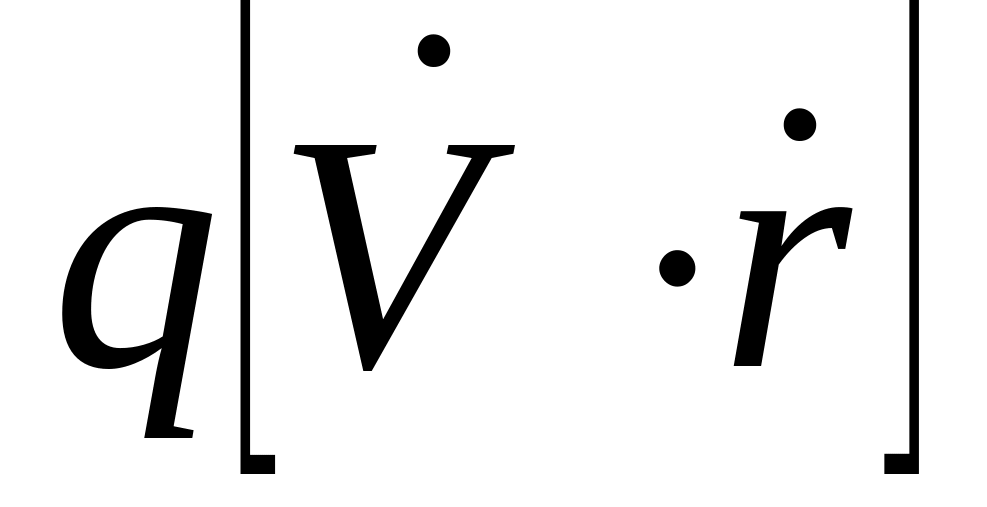3. - пропорционально модулю вектора. Это противоречит опыту – индукция с увеличением расстояния должна уменьшаться, значит нужно добавить такой множитель, чтобы индукция была обратно пропорциональна квадрату расстояния: нужно добавить .

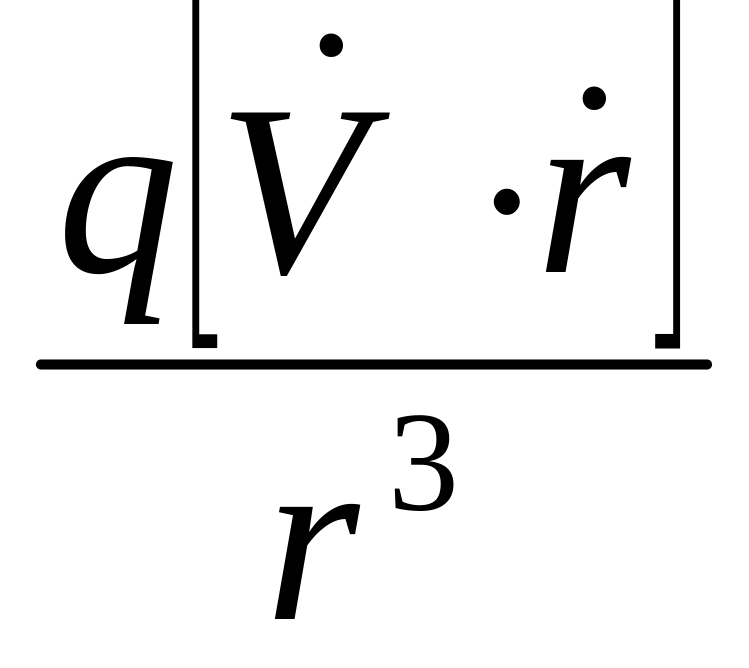Можем записать: . (Эта формула не когерентна, потому что с ее помощью не возможно вывести единицы измерения ).

Вектор направлен таким образом, что если смотреть из острия этого вектора, то поворот вектора до совпадения с происходит в положительном направлении, т.е. против часовой стрелки. Поворот производится по меньшему углу.

Закон Био-Савара-Лапласа.

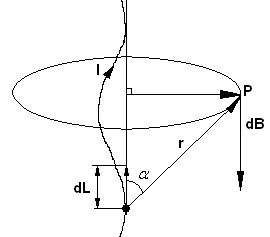
Вычислим индукцию , которая создается элементом проводника в точке Р. По проводнику протекает ток . Сконструируем формулу для вычисления :

.

Эта формула была получена Лапласом на основании экспериментальных данных, которые были получены Био и Саваром. Формула более универсальна и позволяет вычислить индукцию в точке Р в зависимости от конфигурации проводника. В частности, в случае если проводник выполнен в виде прямой, которая лежит в плоскости доски. Тогда индукция в точке Р, расположенной на расстоянии от проводника:

.

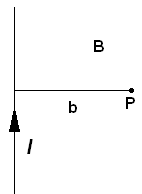
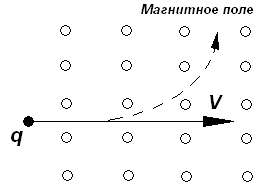
Сила Лоренца.

Установлено, что на заряд, движущийся в магнитном поле, действует сила :

- это формула подвижного заряда,

где заряд;

скорость движения заряда;

индукция.

Т.к. сила действует перпендикулярно скорости, то изменить кинетическую энергию тела, которое несет заряд невозможно. Изменяется только направление движения.

Замечания к формуле:

1. сила является только одной из составляющих сил, действующих на заряд. Если есть электрические и магнитные силы, то суммарная сила:

,

где напряженность эл. поля.

2. это уравнение когерентное – удобное для установления единиц измерения индукции. Если заряд равен 1Кл. и движется со скоростью 1 м/с в равномерном магнитном поле и сила взаимодействия равна 1Н, то индукция магнитного поля принимается равной единице, т.е. 1Тл.

Взаимосвязь основных уравнений.

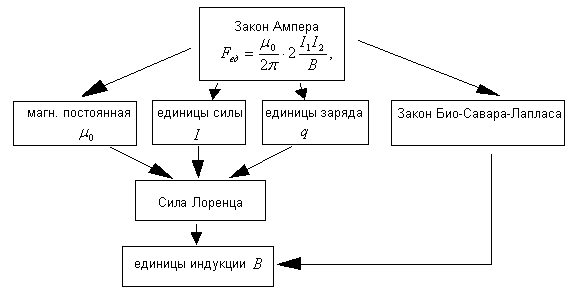
Замечание: Две формулы 1)поле подвижного заряда и 2) Био-Савара-Лапласа взаимосвязаны таким образом, что если принять одно из этих уравнений основным, то другое выводится автоматически. Можно считать, что движение заряда в магнитном поле – это результаты экспериментальных данных, тогда формула Био-Савара-Лапласа выводится автоматически. Из этой формулы видно, что единственным источником магнитного поля является ток (движущий заряд).