1 Магнитное поле в вакууме и его основные характеристики.

1.1 Индукция магнитного поля.

Магнитное поле проявляется в:

• возникновении ЭДС;

• возникновении заряда;

• эффекте Холла.

1.1.1 Опыт с баллистическим гальванометром.

Баллистический гальванометр – магнитоэлектрический механизм, у которого противодействующий момент приблизительно равен нулю, а момент инерции – на много больше, чем у обычных гальванометров.

Таким гальванометром можно измерять заряд, который проходит через его (гальванометра) рамку.

Опыт заключается в следующем:

1) Имеется любой источник магнитного поля (например, катушка). Будем исследовать магнитное поле в точке С.

2) Имеется рамка площадью S, которая соединена с баллистическим гальванометром. Сопротивление цепи r.

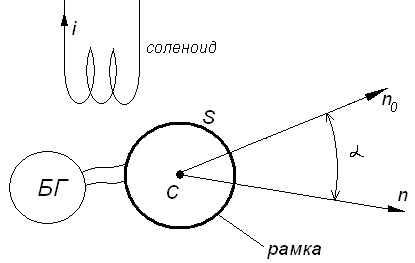
Рамку из исследуемой точки будем перемещать в точку А, в которой магнитное поле практически отсутствует и фиксируем заряд, который покажет БГ.

По результатам серии опытов можно сделать такие выводы:

1. Заряд не зависит от положения т.А (рамку мы можем переместить в любую другую точку, в которой магнитное поле практически отсутствует);

2. Заряд q пропорционален площади рамки S;

3. Заряд обратно пропорционален сопротивлению контура r;

4. Заряд q зависит от исходного положения рамки – т.е. существует такое направление 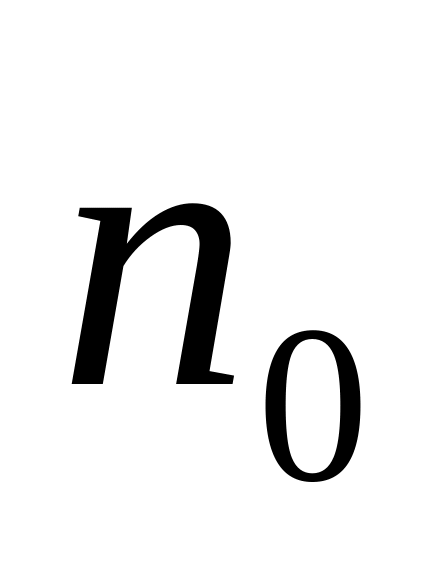, при котором при прочих равных условиях заряд q будет максимальным (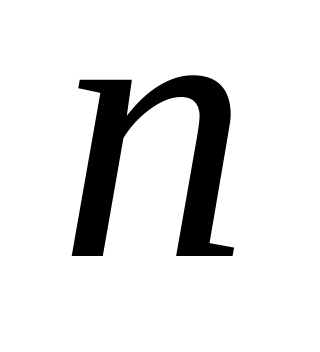 - направление рамки, при котором проводится опыт);

5. Заряд q пропорционален числу витков соленоида.

где В – индукция магнитного поля.

Вектор площади определяется следующим образом:

Модуль вектора равен площади рамки и направлен перпендикулярно площади рамки таким образом, что если смотреть из острия этого вектора, то обход рамки будет в положительном направлении (против часовой стрелки).

Введем новый параметр:

где A – магнитный поток.

Таким образом, векторное поле индукции В порождает скалярную величину – поток магнитной индукции.

.

Если т.А

Разделим уравнение на время, которое нам понадобилось чтоб переместить рамку из т.С в т.А.

,

,

,

,

или с учетом знака:

.

Это одна из форм записи закона электромагнитной индукции (уравнение максвелла). Оно широко используется для измерения индукции и магнитного потока.

Введем еще одну величину – потокосцепление:

где число витков рамки.

.

Попробуем узнать потокосцепление соленоида:

где коэффициент пропорциональности.

Если размер соленоида не изменится под действием тока, тогда не зависит от времени:

Тогда

Таким образом, индуктивность соленоида. Она пропорциональна потоку, сцепленному с соленоидом.

1.1.2 Принцип непрерывности магнитного поля. Формула Остроградского.

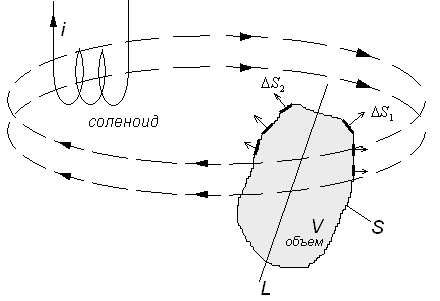
вычислим поток через замкнутую поверхность, имеющую площадь S. Можно провести такую замкнутую линию L таким образом, чтоб в любой точке справа от L линии магнитной индукции входили в этот объем, а слева – выходили.

В каждой части поверхности S выделим очень маленькую площадь . Выберем положительный обход поверхности и представим вектором. Векторы этих площадок всегда направлены от поверхности. Таким образом, вектора и имеют между собой тупой угол. Следовательно, поток, пронизывающий имеет знак «-».

Угол между и - острый, поэтому поток, пронизывающий имеет знак «+».

Для каждой площади справа от линии L найдется площадь слева от линии, так что суммарный поток через эти площадки = 0.

.

Перемещая площадь вдоль линий магнитной индукции мы убеждаемся в том, что для любого положения справедливо уравнение . Это нас приводит к выводу о том, что линии магнитной индукции непрерывны и замкнуты.

Векторное поле, для которого выполняется это уравнение называется соленоидальным, а векторное поле, для которого выполняется это уравнение – вихревым.

Как охарактеризовать способность порождать вектор в каждой точке?

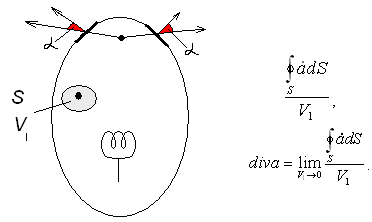
Дивергенция вектора характеризует возможность порождения потока в каждой точке пространства.

Предположим, что у нас есть вектор а, который пронизывает замкнутую поверхность S.

Обозначим объем, ограниченный площадью S как . Введем новую величину, которая равна:

.

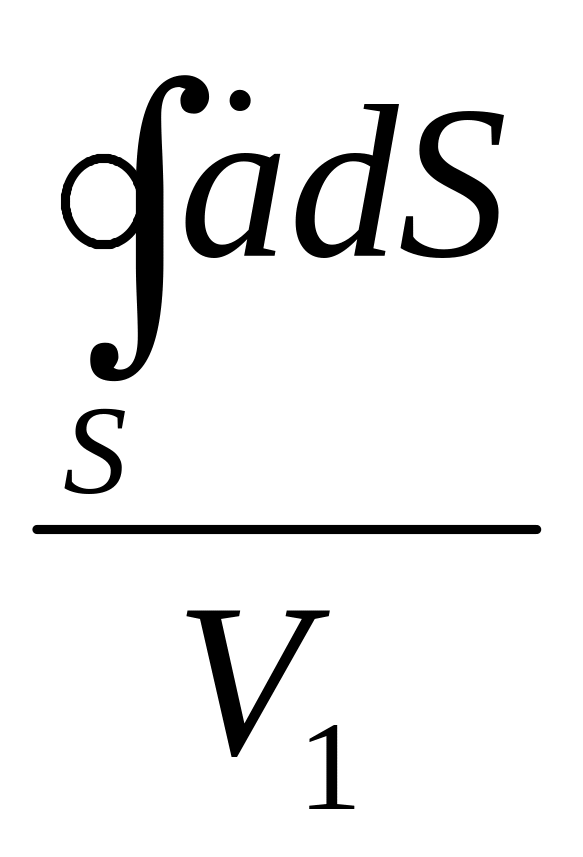Эта величина характеризует способность объема порождать вектор . Устремим к нулю и выведем величину – дивергенция вектора , которая определяется этим уравнением.