7.1 Комплексная магнитная проницаемость.

Погрешность модели заключается в замене динамического цикла эллипсом. Т.е. при измерении потерь погрешность зависит от того, с какой точностью эллипс отображает динамический цикл.

Уравнение эллипса (для нашего случая) можно записать в параметрической форме следующим образом:

(1)

Минус во втором уравнении говорит о том, что индукция всегда отстает от напряженности:

Синусоидальная форма параметрического уравнения эллипса позволяет использовать аппарат векторных диаграмм и аппарат анализа цепей на переменном синусоидальном токе.

Второе уравнение (из системы (1)) можно записать таким образом:

.

Это уравнение позволяет ввести понятие комплексной магнитной проницаемости:

,

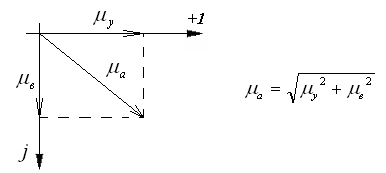
где амплитудная магнитная проницаемость (полная магнитная проницаемость):

;

действительная часть полной магнитной проницаемости. Будем ее называть консервативной или упругой магнитной проницаемостью:

;

мнимая часть полной магнитной проницаемости (еще она называется консумтивной или вязкой):

.

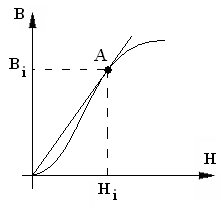
ОКН:

По этому графику можно отметить точку, в которой максимальная магнитная проницаемость.

Если динамический цикл заменим на эллипс:

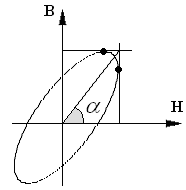
Мы можем показать точку, в которой .

.

Выводы: значение напряженности , значение индукции для эллипсовидной формы динамического цикла наблюдаются в разных точках, следовательно нет точки на кривой динамического цикла, в которой и и достигают максимальных значений.

7.2 Связь комплексной магнитной проницаемости и ее составляющих с потерями на перемагничивание.

Эту связь можно установить из уравнения удельных потерь на перемагничивание, т.е. потерь энергии на единицу объема:

.

Если мы заменили динамический цикл эллипсом:

где ;

.

Первый интеграл = 0, т.к. это – интеграл синусоиды за период Т.

;

.

Вывод из последней формулы: удельные потери на перемагничивание прямопропорциональны вязкой магнитной проницаемости и не зависят от упругой магнитной проницаемости .

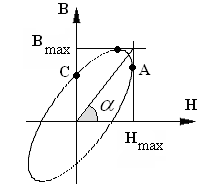
7.3 Связь комплексной магнитной проницаемости и ее составляющих с параметрами эллипса.

Эту связь устанавливаем на основе параметрического задания эллипса:

.

Из уравнения (1) видно, что при .

При этом .

Вычислим отношение отрезков:

.

Таким образом, зная соотношение эллипса, мы можем определить .

= соотношению индукции, соответствующей максимальной напряженности к этой (максимальной) напряженности.

Предположим, что . При этом . Ищем эту точку на эллипсе – это т.С.

Значение индукции в точке, где принято называть остаточной индукцией.

Тогда в этой точке индукция, а точнее ее модуль будет равен:

.

Вывод: вязкая проницаемость равна отношению остаточной индукции к максимальному значению напряженности.

Потери на перемагничивание.

; (1)

. (2)

Уравнение (2) запишем в другом виде:

.

Слагаемое в правой части уравнения умножим и разделим на :

.

С учетом уравнения (1) и выражений для и запишем:

.

При рассмотрении потерь энергии на перемагничивание слагаемое можно не учитывать, т.к. удельные потери определяются только вязкой проницаемостью . Знак минуса тоже не учитываем, потому что потери всегда имеют только положительный знак.

Тогда:

;

;

. (3)

Уравнение эллипса можно записать в следующем виде:

. (4)

Следовательно, разделим и правую и левую часть уравнения (3) на :

. (5)

Сравнив уравнения (4) и (5), получим:

;

.

Известно, что площадь эллипса равна:

, (6)

где удельные потери на перемагничивание.

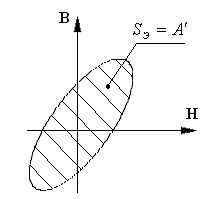
Если есть возможность определить площадь , то по формуле (6) можно рассчитать значение .