4.2 Измерение индукции на переменном токе.

Если мы определяем точку :

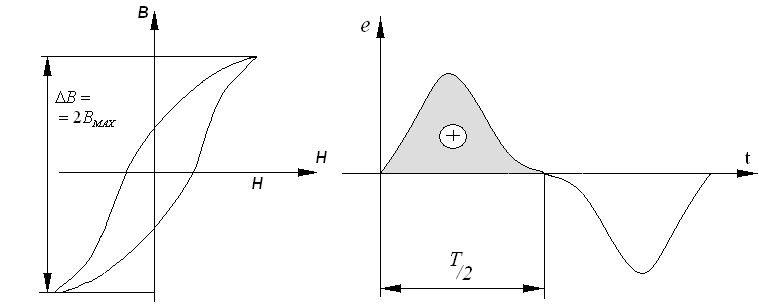
При изменении напряженности от до изменение индукции будет равно:

.

Этому максимальному изменению индукции соответствует максимальное изменение интеграла:

.

Если мы определяем точку :

Это означает, что мы должны проинтегрировать положительную полуволну функции .

.

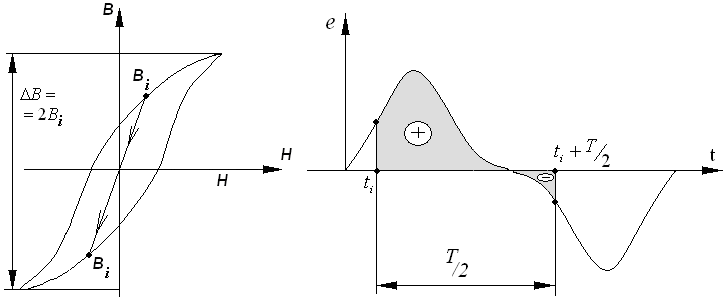
В измерительной обмотке индуцируется ЭДС:

,

.

Вычислим среднее значение напряжения во вторичной обмотке за время, равное половине периода:

.

Из рисунка ясно, что , следовательно:

.

Из последней формулы следует, что среднее значение напряжения во вторичной обмотке пропорционально мгновенному значению индукции.

4.3 Выводы.

1) При синусоидальном токе намагничивания напряжение во вторичной обмотке образца, а в общем случае трансформатора (т.к. он тоже состоит их двух обмоток) не будет синусоидальным.

Для такого преобразования ( на входе и на выходе) необходимо, чтоб коэффициент преобразования должен быть функцией, представляющей собою линейную зависимость:

Но в нашем случае функцией коэффициента преобразования является кривая динамического цикла.

Удельные потери на перемагничивание:

.

Мы знаем, что - не синусоидальна мы можем разложить ее в ряд Фурье, в котором участвуют частоты 1-й, 2-й, n-й гармоники:

Интеграл от выражения - не равен нулю.

Интеграл от выражения - равен нулю.

Функция синуса ортогональна, а это значит, что интеграл:

Следовательно, если намагничивание осуществляется на переменном токе (напряжение синусоидальное), то удельные потери на перемагничивание будут только на первой гармонике, не смотря на то, что - не синусоидальна.

Вывод: тогда для испытания магнитомягких материалов можно использовать компенсатор переменного тока, который работает только на первой гармонике.

Зададимся вопросом: какая должна быть цепь для того, чтоб была синусоидой?

Необходимо, чтоб сопротивление цепи везде было одинаковым (т.е. линейным, т.е. независимым). Но образец не имеет постоянного сопротивления. Чтоб сопротивление было постоянным надо в цепь поставить большое сопротивление.

2) Значение индукции и напряженности достигают своих максимальных значений в разные моменты времени:

если учесть только первую гармонику индукции , то

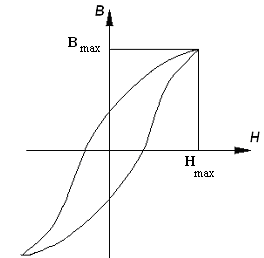
превращается в

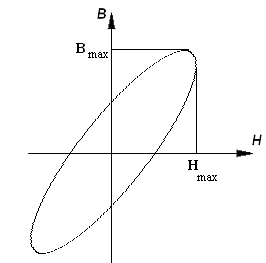
Построим феррометр:

Зависимость :

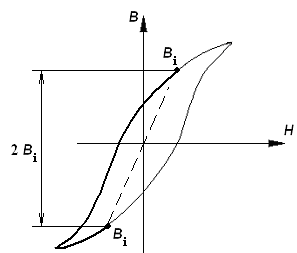
Зависимость :

Для этого мы используем катушку взаимной индуктивности:

.

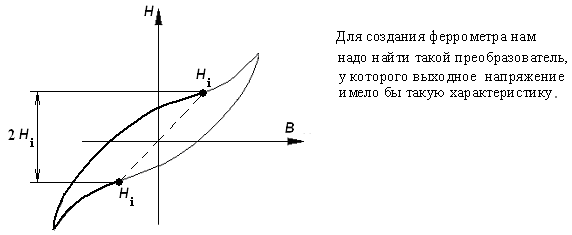
4.3 Измерение напряженности.

Используя одну и ту же форму уравнения:

• ЭДС во вторичной обмотке катушки взаимной индуктивности:

,

где взаимная индуктивность;

мгновенное значение тока в первичной обмотке.

• ЭДС во вторичной обмотке образца:

.

Можно измерить мгновенное значение тока в намагничивающей обмотке и, следовательно, мгновенное значение напряженности, используя фазочувствительный вольтметр, т.е. вольтметр с управляемым началом генерирования.

Таким образом, феррометр представляет собой два одинаковых вольтметра средних значений, причем начало интегрирования этих вольтметров выбирается одинаковым. Тогда показания одного вольтметра будут пропорциональны индукции, а показания второго – напряженности.

Для измерения напряженности используем катушку взаимной индуктивности, ЭДС вторичной обмотки которой:

,

где взаимная индуктивность;

мгновенное значение тока в первичной обмотке.

Тогда среднее значение напряжения за время интегрирования, равное периода:

,

где начало интегрирования.

С учетом закона полного тока, запишем:

;

;

;

.