3.5.2.2 Применение бг для испытания магнитомягких материалов.

На рисунке обозначено:

число витков измерительной обмотки;

сопротивление в цепи БГ (т.е. сумма сопротивления БГ, сопротивления образца и сопротивления обмотки);

переменное сопротивление, позволяющее выбрать режим работы.

,

где удельный противодействующий момент;

коэффициент успокоения;

момент инерции.

изменяется в зависимости от суммарного сопротивления в цепи БГ ( ). Для того, чтоб установить режим БГ указывается внешнее критическое сопротивление .

1) Если (не учитывается сопротивление обмотки), то будет критический режим, т.е. .

2) Если , то режим периодический, .

3) Если , то режим апериодический, .

При измерении потокосцепления в обмотке возникает ЭДС, которая, в соответствии со вторым законом Кирхгофа, уравновешивается падением напряжения на активном сопротивлении и ЭДС самоиндукции в обмотке :

, (4)

где индуктивность вторичной обмотки .

С другой стороны, мы знаем, что ЭДС ( ) связана с потокосцеплением следующим уравнением, где левая часть взята по модулю:

(5)

Подставим уравнение (5) в (4) и проинтегрируем полученное уравнение за время (где время изменения потокосцепления):

.

Второе слагаемое в правой части равно нулю, т.к. в момент , а после коммутации (в момент времени ) :

.

Потокосцепление прямо пропорционально числу витков :

,

.

Поток пропорционален .

Обозначим:

,

где постоянная БГ по потоку.

Получим:

.

Учтем, что ,

где площадь сечения образца.

И окончательно получим:

.

Таким образом, мы доказали, что с помощь БГ можно измерить изменение индукции, которое пропорционально первому максимальному отклонению БГ.

Чувствительность и, следовательно, можно изменять с помощью сопротивления .

3.5.2.3 Определение постоянной бг.

Т.к. постоянная зависит от конструктивных параметров гальванометра ( ) а также от значения сопротивления , то перед использованием БГ возникает необходимость экспериментального определения постоянной БГ.

В качестве меры магнитного потока используется катушка взаимной индуктивности.

Схема эксперимента:

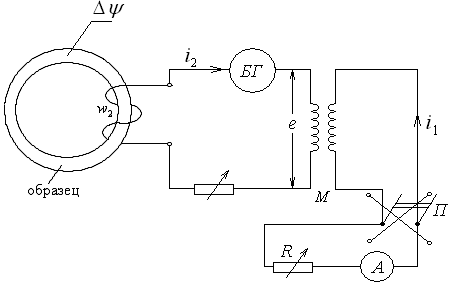
На рисунке обозначено:

взаимная индуктивность;

переключатель (изменяет полярность тока в первичной обмотке ).

При коммутации первичного тока во вторичной обмотке возникает ЭДС:

.

Эта ЭДС уравновешивается падением напряжения на активном сопротивлении цепи БГ ( ) и ЭДС самоиндукции индуктивности в цепи БГ:

,

где ток в цепи гальванометра;

суммарное сопротивление в цепи БГ;

суммарная индуктивность.

Проинтегрируем это уравнение за время коммутации :

.

Т.к. ток в момент времени и в момент времени равен нулю, то , тогда:

.

Откуда получим:

, (6)

где изменение тока .

Формула (6) позволяет экспериментально определить постоянную БГ перед испытаниями магнитомягких материалов.