Уравнения жесткости конечного элемента

Рассмотрим сначала линейно-упругую задачу деформирования твердого тела при малых деформациях и малых перемещениях. Принимается, что конечные элементы взаимодействуют только через общие узлы. Внутренние распределенные силы, действующие по границам элемента е, заменяются статически эквивалентными узловыми силами, составляющими вектор узловых сил элемента . Внешние распределенные массовые и поверхностные силы, действующие на конечный элемент, приводятся к статически или энергетически эквивалентным узловым силам, образующим соответственно векторы и 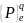. К эквивалентным узловым силам приводятся также силы инерции (как массовые силы), начальные деформации, в том числе начальные напряжения (вектор ).

Матричное уравнение жесткости элемента имеет вид:

где матрица жесткости элемента, состоящая из коэффициентов жесткости;

вектор узловых перемещений элемента.

Обоснование уравнения (3) может быть выполнено с помощью теории упругости или сопротивления материалов, но такой подход имеет ряд недостатков [3]. Более эффективными и во многих случаях более корректными способами обоснования уравнений жесткости элементов являются вариационные методы и методы невязок [1 — 9]. Заметим, что вариационные методы позволяют получать общую систему уравнений равновесия всей модели без введения узловых сил , то есть без предположения о взаимодействии элементов только через узлы и без составления соотношений (3) для жeсткости элементов. Однако в вычислительном процессе МКЭ удобно вначале определять матрицы элементов , а затем из них собирать общие матрицы системы уравнений равновесия модели по стандартным правилам суммирования компонентов матриц с одинаковыми индексами.

Если задача деформирования динамическая, то, в уравнение (3) добавляются узловые силы, эквивалентные массовым силам инерции, зависящим от ускорения. Демпфирование учитывается эквивалентными объемными силами вязкого сопротивления, пропорциональными скорости. В результате получается дифференциальное матричное уравнение:

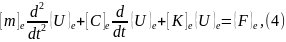
где матрица демпфирования элемента, зависящая от коэффициента вязкого демпфирования ;

матрица масс элемента, зависящая от плотности материала элемента .

Разрешающие уравнение мкэ

Из условий равновесия узлов или с помощью вариационных принципов, а также методов невязок, применяемых ко всей конечно- элементной модели, составляется общая система уравнений равновесия всей конечно-элементной модели исследуемого деформируемого тела. Для статических задач она имеет вид:

где общая (глобальная) матрица жесткости конечно-элементной модели;

{ Р } общий вектор заданных внешних узловых сил;

общие (глобальные) векторы узловых сил, эквивалентных распределенным поверхностным и массовым силам, начальным деформациям, начальным напряжениям.

Компоненты матрицы являются коэффициентами жесткости модели. Они вычисляются путем суммирования соответствующих коэффициентов жесткости конечных элементов. Матрица жесткости для конечно-элементной модели обладает симметрией, имеет ленточную структуру и редкое заполнение.

Общий вектор заданных внешних узловых сил {Р} можно пред­ ставить в виде:

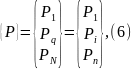
где подматрица из n₁ компонентов силы, приложенной в узле i. Для трехмерной задачи будем иметь . Как видно из выражения (6), индексация компонентов может быть или по общим номерам степеней свободы модели или по общим номерам узлов с добавлением индекса узловой степени свободы, как у общего вектора узловых перемещений (2).

Общие (глобальные) векторы узловых сил собираются из компонентов соответствующих элементных векторов. Их структура такая же, как у вектора .

В динамических задачах на основании принципа Даламбера в уравнения (5) добавляются силы инерции. Так как силы инерции выражаются через ускорения, которые являются вторыми производными от перемещений, то уравнения равновесия (5) превращаются в общие (глобальные) дифференциальные уравнения движения, в которых внешние силы могут быть переменными:

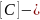где и общие (глобальные) матрицы масс и демпфирования модели, которые собираются из компонентов соответствующих элементных матриц.

С помощью уравнений (7) выполняются различные виды динамического анализа: модальный анализ, где определяются собственные частоты и формы конструкций; гармонический анализ, где определяется отклик системы на внешнюю периодическую силу с различной частотой; полный анализ динамического процесса, где производится интегрирование дифференциальных уравнений движения.

В статических задачах задаваемые перемещения (связи) должны исключать возможность перемещения нагруженной конструкции как абсолютно твердого тела. Только в этом случае разрешающая система уравнений (5), после учета граничных условий, будет иметь единственное решение. До учета связей исходная система (5) имеет линейно зависимые уравнения, определитель ее матрицы жесткости равен нулю, следовательно, матрица жесткости свободного тела является сингулярной, и нельзя найти однозначного решения для узловых перемещений. [5, 7] Динамические задачи, описываемые уравнениями (7), могут решаться без наложения связей - перемещений.