2. В процессе измерений

а) способ замещения – метод сравнения с мерой. в котором измеряемую величину замещают мерой с известным значением величины.  Объект заменяется образцовой мерой, находящейся в тех же условиях, что и сам объект (это одна из модификаций метода сравнения);

б) способ компенсации погрешности по знаку  измерения проводят дважды так, чтобы не известная по величине, но известная по своей природе погрешность входила в результат измерения с противоположным знаком, и находят полусумму этих результатов. Так исключают погрешность из-за трения, люфта и т.д. Разновидность – метод противопоставления;

в) способ симметричных наблюдений  измерения проводят последовательно через одинаковые интервалы изменения аргумента. За окончательный результат принимается среднее значение любой пары симметричных наблюдений относительно середины интервала измерений. Погрешности от температуры, давления, времени, ...;

г) способ рандомизации, т.е. перевод систематических погрешностей в случайные.

Пусть имеется n однотипных приборов с систематическими погрешностями одинакового происхождения. От прибора к прибору погрешность меняется случайным образом. Следовательно, можно произвести измерения разными приборами и усреднить результаты.

3. После проведения измерений. При обработке результатов могут быть исключены систематические погрешности с известными значениями и знаками. Для этого в неисправленные результаты наблюдений вводятся поправки или поправочные множители. После внесения поправок получается исправленный результат измерения – полученное при измерении значение величины и уточненное путем введения в него необходимых поправок на действие систематических погрешностей.

Поправка – это значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности: q=-_C; Х=Х́+q, где Х́ – неисправленный результат.

Поправочный множитель – числовой коэффициент, на который умножают неисправленный результат измерения с целью исключения влияния систематической погрешности: Х=Х́.

1.3. Случайные погрешности и обработка результатов измерений

1.3.1. Распределения случайных величин и их числовые характеристики

Вследствие того, что результат измерения Х содержит случайную погрешность , он сам является случайной величиной.

Основной характеристикой случайной величины является функция распределения вероятностей, которая устанавливает связь между возможными значениями случайной величины и вероятностями их появления при многократных измерениях.

Существуют две формы представления этой функции: интегральная и дифференциальная.

Интегральной функцией распределения результата наблюдений является функция F(х) – вероятность того, что результат наблюдения Х окажется меньше некоторого текущего значения х: F(х)=Р{Х<х}.

Это положительная неубывающая функция (рисунок 1.3.1):

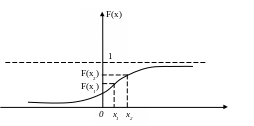
Рисунок 1.3.1 – Интегральная функция распределения результатов наблюдений

Основное свойство этой функции: вероятность того, что случайная величина принимает значения в интервале {х₁, х₂}, равна разности значений функции на концах интервала:

Р{х₁Х х₂} = F(х₂) - F(х₁).

Если обозначить приращение х₂ - х₁=х, то одинаковым приращениям х соответствуют различные значения приращения вероятности F(х). Тогда можно ввести понятие плотности распределения вероятностей случайной величины, или плотности вероятностей, которая будет иметь следующий вид:

.

Функции распределения достаточно полно могут быть определены своими числовыми характеристиками, к которым относятся начальные и центральные моменты.

Начальным моментом является математическое ожидание случайной величины степени:

, где

n – количество наблюдений.

В большинстве случаев начальный момент 1 порядка совпадает с истинным значением измеряемой величины.

Центральный момент к-порядка - математическое ожидание к-й степени центрированной случайной величины (т.е. разности между значением случайной величины и ее математическим ожиданием). Применительно к измерениям центрированная случайная величина будет случайной погрешностью:

 = = Х - Q .

Оценка математического ожидания будет состоятельной, несмещенной и эффективной оценкой истинного значения физической величины.

Состоятельной называют оценку, которая приближается к истинному значению измеряемой величины при n .

Несмещенной называется оценка, математическое ожидание которой равно истинному значению оцениваемой величины.

Эффективной является несмещенная оценка, для которой дисперсия минимальна.

Центральным моментом 2 порядка будет дисперсия результатов наблюдений:

.

Это рассеяние результатов наблюдений относительно математического ожидания. Недостаток такого представления погрешности измерения заключается в том, что она имеет размерность квадрата измеряемой величины. Поэтому на практике используют значение среднеквадратического отклонения результата измерения

.

В отличие от результатов измерения, числовые характеристики функции распределения являются детерминированными, а не случайными. Следовательно, чтобы найти точные значения, необходимо произвести бесконечно большое число наблюдений. Отсюда возникает задача определения приближенных значений, полученных в некотором количестве независимых наблюдений. В математической статистике такие приближенные значения, выраженные одним числом, называются ТОЧЕЧНЫМИ ОЦЕНКАМИ. Любая точечная оценка, вычисленная на основе опытных данных, представляет собой случайную величину, зависящую от самого оцениваемого параметра и от числа опытов. Распределение оценки зависит от распределения исходной случайной величины. Оценки классифицируются следующим образом:

- состоятельные, когда при увеличении числа наблюдений они приближаются к значению оцениваемого параметра;

- несмещенные, если математическое ожидание равно оцениваемому параметру;

- эффективные, если ее дисперсия меньше дисперсии любой другой оценки этого параметра.