
- •Определение производной. Ее физический смысл. Определение дифференцируемой функции. Сформулировать теорему о связи между дифференцируемостью и непрерывностью функции.
- •Геометрический смысл производной. Уравнения касательной и нормали
- •Теорема о дифференцировании суммы, произведении, частного (доказать для суммы).
- •Сформулировать теорему о дифференцировании обратной функции
- •Дифференцирование основных элементарных функций.
- •Логарифмическое дифференцирование
- •Дифференцирование параметрически заданных функций.
- •Понятие дифференциала функции, его формы записи.
- •Геометрический смысл и свойства дифференциала.
- •Производные высших порядков. Вторая производная функции, заданной параметрически
- •Сформулировать теоремы Ролля и Коши. Геометрический смысл теоремы Ролля.
- •Теорема Лагранжа. Ее геометрический смысл. Сформулировать следствия из теоремы Лагранжа.
- •Определения возрастающей, убывающей, монотонной функции. Сформулировать необходимое условие монотонности функции. Достаточное условие монотонности функции.
- •Определения точек максимума, минимума и экстремума функции. Сформулировать необходимое условие экстремума. Критические точки.
- •Достаточное условие экстремума
- •Определение точки перегиба графика функции. Необходимое условие точки перегиба
- •Определение
- •Определение точек, «подозрительных на перегиб». Достаточное условие точки перегиба
- •Определение асимптоты графика функции. Виды асимптот. Уравнения асимптот
- •Определение первообразной. Сформулировать теоремы о существовании первообразной и о виде первообразной
- •Неопределенный интеграл. Его свойства. Таблица неопределенных интегралов
- •Метод подведения под знак дифференциала и замены переменной
- •Метод интегрирования по частям
- •Интегрирование дробно-рациональных функций. Интегрирование простых дробей
- •Задача о площади криволинейной трапеции
- •Понятие определенного интеграла. Его свойства
- •Интеграл с переменным верхним пределом. Сформулировать теорему Барроу. Формула Ньютона-Лейбница Интеграл с переменным верхним пределом
- •Способы вычисления определенного интеграла: интегрирование по частям, замена переменной, интеграл, взятый по симметричному интервалу
- •Вычисление площади плоской фигуры в декартовой и полярной системах координат
- •Вычисление длины кривой
Сформулировать теоремы Ролля и Коши. Геометрический смысл теоремы Ролля.
(Теорема Ролля) Пусть функция f(x)
непрерывна на отрезке [a, b];
дифференцируема в интервале (a, b);
на концах отрезка [a, b] принимает равные значения.
Тогда существует точка c (a, b) такая, что f'(c) = 0.
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 118.
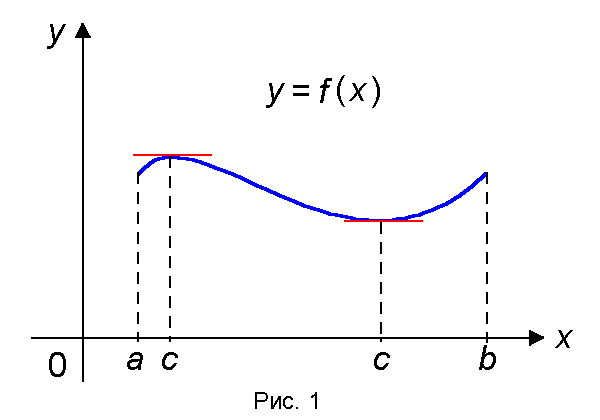
Геометрическая интерпретация теоремы Ролля
Из теоремы Ролля следует, что существует точка с (a, b), в которой касательная к графику функции f(x) параллельна оси ОX (рис. 1).
(Теорема Коши) Пусть функции f(x) и g(x)
непрерывны на отрезке [a, b];
дифференцируемы в интервале (a, b);
x (a, b) g'(x) ≠ 0 .
Тогда существует точка c (a, b) такая, что
|
=
. |
(3) |
Формула (3) называется формулой Коши.
Теорема Лагранжа. Ее геометрический смысл. Сформулировать следствия из теоремы Лагранжа.
(Теорема Лагранжа) Пусть функция f(x)
непрерывна на отрезке [a, b];
дифференцируема в интервале (a, b).
Тогда существует точка с (a, b) такая, что
|
f(b) − f(a) = f '(c) · (b − a) . |
(1) |
Формула (1) называется формулой Лагранжа, или формулой конечных приращений
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 119.
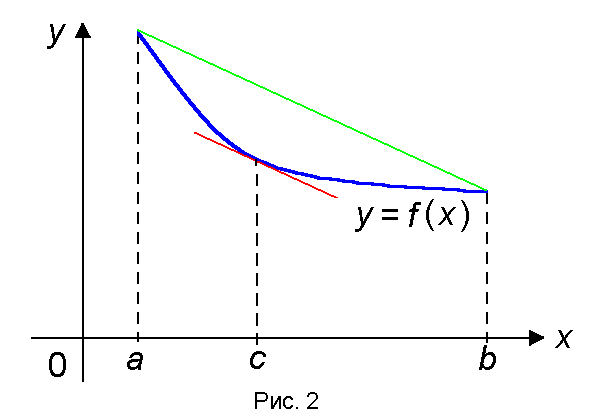
Геометрическая интерпретация теоремы Лагранжа
Представим формулу (1) в виде
|
= f '(c) . |
(2) |
Число
f(b) − f(a) |
b − a |
есть угловой коэффициент прямой, проходящей через концы графика функции y = f(x) — точки (a, f(a) ) и (b, f(b) ), а f '(c) — угловой коэффициент касательной к этому графику в точке (c, f(c) ). Из формулы (2) следует, что существует точка с (a, b), в которой касательная к графику функции f(x) параллельна прямой, проходящей через концы графика (или совпадает с ней) (рис. 2).
Следствие 1. Пусть f(x) - непрерывна на [a;b] ,диф-ма на (a;b) и в каждой точке интервала её производная равна нулю, то f(x) - const.
Следствие 2.
Пусть функции f(x) и g(x) непрерывны на [a;b] и диф-мы на (a;b), и пусть на (a;b) :
f '(x)=g '(x),следовательно f(x) = g(x) +c;
Следствие 3. Пусть f(x) и g(x) непрерывны на [a;b] и диф-мы на (a;b), то если f(a)>=g(a) и для любого x, принадлежащнего(a;b) f ' (x)>=g'(x), следовательно для любого x ,принадлежащего (a;b], f(x)>=g(x).
Замечание:если одно из исходных неравенств строго, то f(x) >g(x).
Правило Лопиталя.
Правило
Лопиталя представляет
собой метод вычисления пределов, имеющих
неопределенность
типа ![]() или
или ![]() .
Пусть a является
некоторым конечным действительным
числом или равно бесконечности.
.
Пусть a является
некоторым конечным действительным
числом или равно бесконечности.
Если
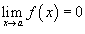 и
и  ,
то
,
то 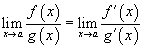 ;
;Если
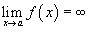 и
и 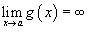 ,
то аналогично
.
,
то аналогично
.
Правило
Лопиталя можно также применять к
неопределенностям типа ![]() .
Первые две неопределенности
.
Первые две неопределенности ![]() можно
свести к типу
или
с
помощью алгебраических преобразований.
А неопределенности
можно
свести к типу
или
с
помощью алгебраических преобразований.
А неопределенности ![]() сводятся
к типу
сводятся
к типу ![]() с
помощью соотношения
с
помощью соотношения
![]()
