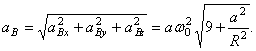3) Скорость точек тела.

По теореме Даламбера-Эйлера за малое время движение тела можно представить как вращение вокруг неподвижной оси с некоторой угловой скоростью (рис.23).

Рис.23

 

Тогда скорость точки : В пределе, при , угловая скорость будет приближаться к мгновенной угловой скорости , направленной по мгновенной оси вращения , а скорость точки - к истинному значению:

.

Но таким же образом находится скорость точки при вращении тела вокруг оси, по которой направлен вектор , в нашем случае – по мгновенной оси вращения . Поэтому скорость точки можно определить как скорость её при вращении тела вокруг мгновенной оси . Величина скорости (рис.23).

Рис. 9.9.

 Определение скоростей то­чек тела значительно упроща­ется, если извест­на мгновенная ось вращения . Иногда её можно найти, если уда­стся обна­ружить у тела хотя бы ещё одну точку, кроме , скорость кото­рой в данный момент равна нулю, и провести ось из не­подвижной точки О через эту точку. Так как мгновенная ось вращения – геометрическое ме­сто точек, скорости которых равны нулю в данный момент времени.

Пример 6. Водило , вращаясь вокруг вертикальной оси с угловой скоростью , застав­ляет диск радиуса кататься по горизон­тальной плоскости (рис.24).

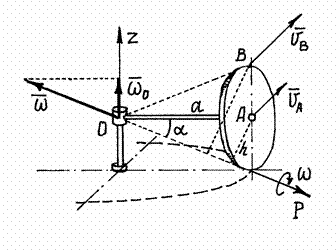
Рис.24

 

Рис. 9.10.

 Если представить диск как ос­нование конуса с вершиной в не­подвиж­ной точке , то движение диска можно назвать вращением вокруг этой неподвижной точки .

Так как скорость точки касания диска с плоскостью равна нулю, то мгновенная ось вращения проходит через эту точку. И вектор мгновенной угловой скорости будет направлен по этой оси.

Точка вместе с водилом вращается вокруг оси . Поэтому её ско­рость (рис.24). Эта скорость определяет направление вращения диска вокруг оси и направление вектора . Величина угловой ско­рости (h – рас­стояние от до оси ). Теперь можно найти скорость любой точки диска, рассматривая его движение как вращение вокруг оси . Так, например, скорость точки : . Так как и , то и

 

4) Ускорение точек тела.

Сначала определим угловое ускорение тела . При движении тела вектор угловой скорости изменяется и по величине, и по направлению. Точка распо­ложен­ная на его конце будет двигаться по некоторой траектории со скоростью (рис.25).

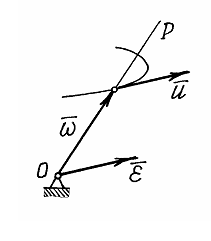
Рис.25

 

Если рас­сматривать вектор как ра­диус-вектор этой точки, то .

Итак. Угловое ускорение тела можно опреде­лить как скорость точки, расположенной на конце вектора угловой скорости:

.

Этот результат называется теоремой Резаля.

Теперь обратимся к определению ускорения точек. Ускорение какой-либо точки тела

,

есть сумма двух векторов.

Первый вектор . Модуль его , где h₁ – расстояние от точки до вектора . Направлен он перпендику­лярно и . Но таким же способом определяет­ся касательное ускорение. Поэтому первую состав­ляющую ускорения определяют как ка­сательное ускорение, предпола­гая, что тело вращается вокруг оси, совпадающей с векто­ром . И обо­значается этот вектор ускорения так

Второй вектор Модуль его , но , т.к. векторы и перпендикулярны друг другу.

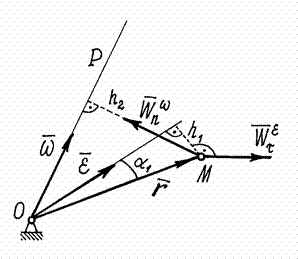
Рис.26

 

Значит , где h₂ – расстояние от точки М до мгновенной оси , до вектора .

Направлен вектор перпендикулярно и , т.е. так же как вектор нормального ускорения при вращении вокруг оси , или вектора . Поэтому этот вектор ускорения и обозначают, соответственно, так:

Итак, ускорение точек тела, вращающегося вокруг неподвижной точки, определяется как сумма двух ускорений:

Этот результат называется теоремой Ривальса.

Заметим, что в общем случае векторы и не совпадают и угол между и не равен , векторы не перпендикулярны друг другу, как это было при вращении тела вокруг неподвижной оси.

 

Пример 7. Продолжим исследование движения диска (пример 6). Модуль угловой скорости Значит вектор вместе с осью , которая всегда проходит через точку касания диска с плоскостью, вращается вокруг оси и описывает конус. Точка М на конце вектора движется по окружности радиуса с угловой скоро­стью . Поэтому угловое ускорение диска .

Откладывается вектор из неподвижной точки О. Направлен он, как скорость , перпендикулярно водилу , параллельно оси х (рис. 27).

Рис.27

 

Найдём ускорение точки В.

Ускорение Направлен вектор перпендикулярно и расположен в плоскости .

Ускорение Вектор направлен по , перпендикулярно мгновенной оси . Модуль вектора найдём с помощью проекций на оси :

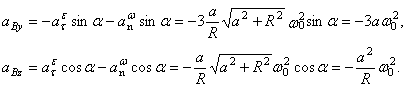
Значит