Курсовая работа по электродинамике

1. Задача 1.100

Рассмотрим бесконечную заряженную полосу на плоскости xOy. Полоса вытянута вдоль оси Оу и занимает положение [-a,a] по иси Ох. Заряд на елиницу длины полосы равен τ. Найти потенциал поля, создаваемого заряженной полосой в точках плоскости xOy.

Решение:

Рассмотрим пластину длины L, где a<<L

Тогда площадь пластины равна S= 2La, тогда получим:

, так как по условию

(*), тогда потенциал поля создаваемого заряженной полосой в точках плоскости хОу выражается формулой

,

подставляя выражение полученное из (*) получаем:

(**)

Заметим что в точках x=a и x=-a функция имеет перегиб, в чем легко убедиться если извлечь первые и вторые производные из (**)

1. Задача 2.12

Металлические концентрические сферы с радиусами и (<) имеют заряды и . Опишите распределение заряда на сферах. Найдите напряженность и потенциал поля , созданного сферами. Постройте схематично графики зависимостей (r) и (r) следующего случая:

=–2q; =–3q;

Решение:

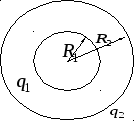
Используем запись теоремы Гаусса для центрально-симметричного случая, где в качестве поверхности взята сфера:

Для потенциала будем иметь:

(*)

Рассмотрим 3 случая:

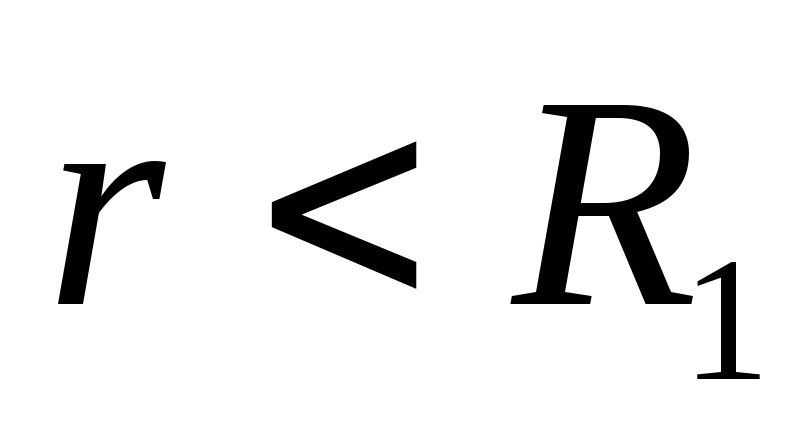1. , тогда получаем

Следовательно , т.е. .

Отсюда .

2. 

По теореме Гаусса:

Из формулы (*) получаем:

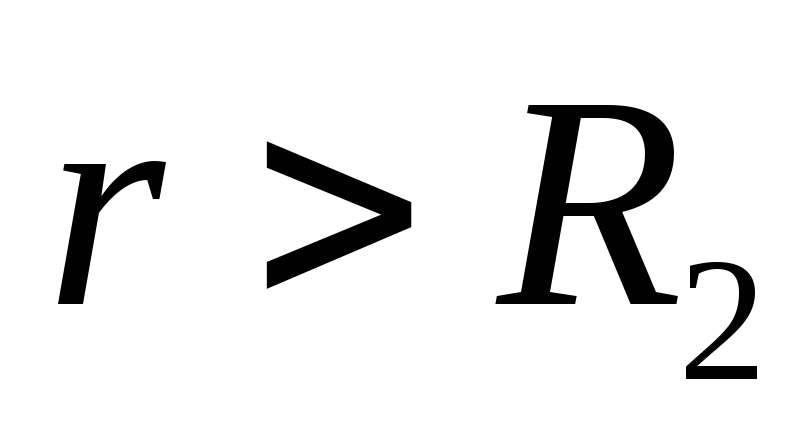3. , получим

Соединив воедино формулы мы получим:

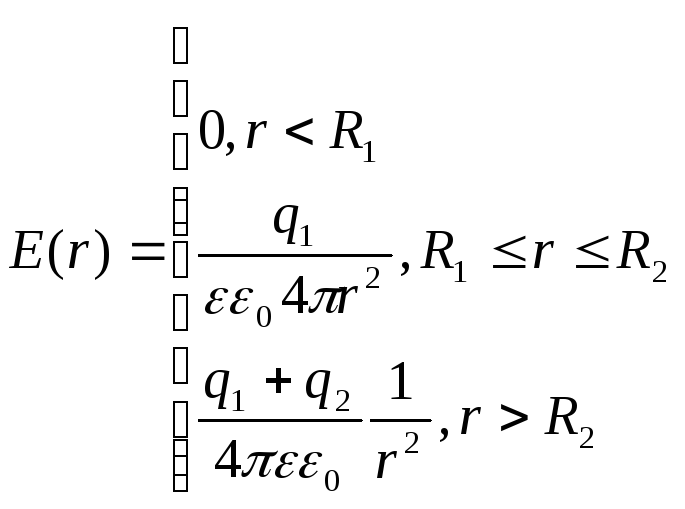
(2.8)

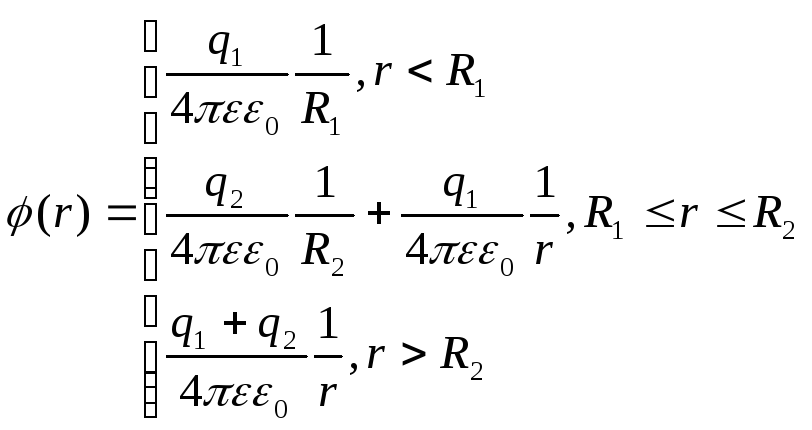
Теперь воспользуемся условием =–2q; =–3q, получим:

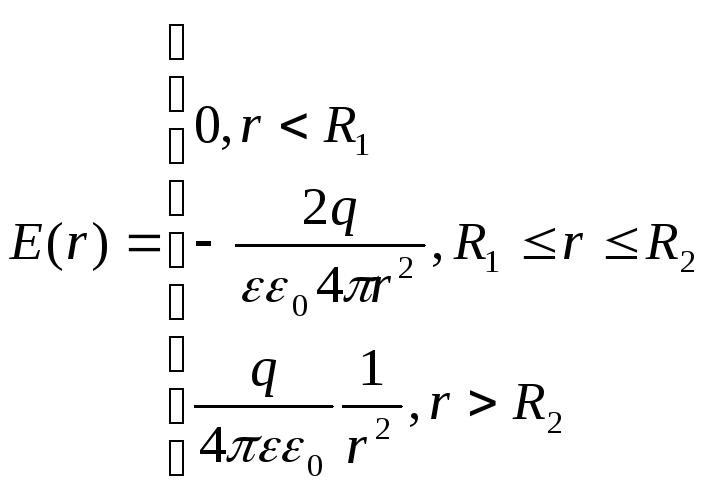
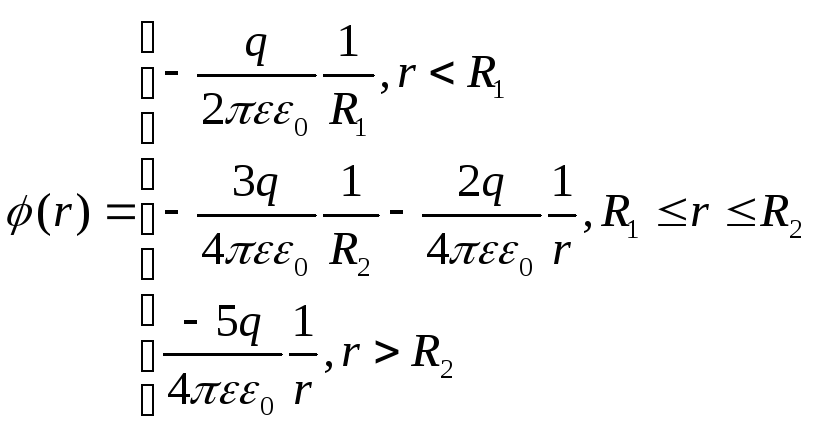
Построим график зависимости (r)