Свойства многомерного нормального распределения

Все одномерные плотности вероятности - это плотности вероятности одномерной нормальной случайной величины с параметрами, определяемыми координатами вектора X и главной диагональю ковариационной матрицы B. Кроме того, подвектор вектора из kэлементов, где также распределен нормально.

Если все коэффициентыкорреляционной или ковариационной матрицы B(все ее недиагональные элементы) равны нулю, то показать самим, что компоненты случайной величины являются независимыми.

если ,то многомерная плотность распадается на произведение одномерных, значит независимы.

Теорема.

Проводим линейное преобразование Y=AX. A -квадратная невырожденная матрица, тогда вектор Yтакже имеет n-мерное нормальное распределение вида

Следствие: Из доказательства теоремы вытекает, что ковариационная матрица

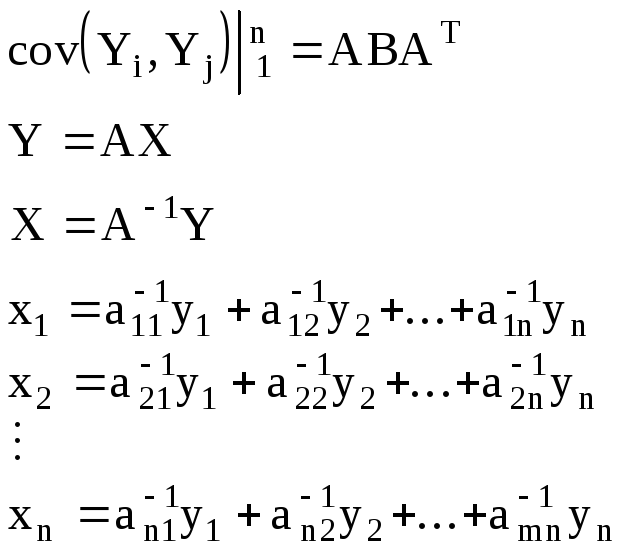
Оператор Aпереводит произвольную область из арифметического пространства R_nв некоторую область того же пространства.

Рассмотрим произвольную область S,принадлежащую пространству элементарных событий случайной многомерной величины X. Ей соответствует область Dв пространстве элементарных событий случайного вектора Y.При этом

Запишем эти вероятности

где |I| - якобиан перехода

Т.к. область Sи соответственно Dпроизвольны, то плотность вероятности случайного вектора xравна

n-мерная плотность вероятности случайного вектора Yравна

Преобразуемпоказатель степени e

Можно показать, что если нормальное распределение имеет данный вид, то B -ее ковариационная матрица

Следствие.

- многомерный нормальный вектор. A -прямоугольная матрицаТогда Y=AXимеет нормальное распределение вида

Y - m-мерный вектор.

Для определенности положим, что матрица Aимеет вид

A = (A₁ A₂)

A₁ - квадратная матрица размером

A₂ - матрица размерности

Рассмотрим матрицу размерности . Считается, что mпервых столбцов независимы.

равен определителю полученной квадратной матрицы и не равен нулю.

E - единственная квадратная матрица размерности

Следовательно, на основании доказанной теоремы, вектор Yимеет многомерное нормальное распределение.

Z=CX

Компоненты вектора Zимеют вид

Пусть матрица А произвольная, но т.к. ее ранг равен m она содержит m линейно независимых столбцов. Путем перестановки столбцом соберем эти столбцы в первые m. И соответствующим образом пронумеруем компоненты вектора Х. Попадаем в предыдущий случай.

Предельные случайные последовательности.

Рассмотрим вероятностное пространство в котором задана счетная последовательность случайных величин, каждая из которых является измеримой

Покажем, что событие измеримо, т.е. имеет вероятность наступления. Действительно событие

Каждое из этих событий в пересечении принадлежит - алгебре. По определению - алгебры ей принадлежит и счетное перечисление этих событий, таким образом событие имеет вероятность наступления.

Пусть последовательность имеет предел при , который может быть постоянной или случайной величиной. В теории вероятности этот предел понимают следующим образом: под сходимостью последовательности к пределу понимают событие А которое может задаваться следующим образом:

1.

Событие А состоит из всех m, удовлетворяющих условию: для любого как угодно большого rсуществует такое m, что для всех n выполняется

2. А: Если предел ,то

Для любого, как угодно большого r существует такое m, что для всех n выполняется

3.Если предел случайная величина, то

Показать самим, что событие А с - алгебре и следовательно имеет вероятность наступления

любое событие измеримо, как доказывалось ранееизмеримы, и следовательно имеет вероятность наступления. Разность -алгебре. Следовательно событие А имеет вероятность наступления.

Если предел константа, то эквиваленты 1 и 2, если случайная величина - то 1 и 3.