Инфинитные орбиты

При r, стремящемся к бесконечности, ζ стремится к −¹⁄₁₂. Поэтому орбиты, неограниченно удаляющиеся или приближающиеся из бесконечности к центральному телу, соответствуют периодическим решениям, в которых -1/12 попадает в доступный ζ интервал, то есть при e₃ ≤ −¹⁄₁₂ ≤ ζ ≤ e₂.

Асимптотически круговые орбиты

Другой специальный случай соответствует −e₃ = 2e₂ = 2e₁, то есть два корня G(ζ) положительны и равны друг другу, а третий — отрицателен. Орбиты в таком случае представляют собой спирали, скручивающиеся или накручивающиеся при стремлении φ к бесконечности (не важно, положительной или отрицательной) на окружность радиуса r, определяемого соотношением (16)

(16)

Обозначив повторяющийся корень e = n²/3, получаем уравнение орбиты, которое легко проверить непосредственной подстановкой:

В таких случаях радиальная координата частицы заключена в пределах 2r_s—3r_s.

Уравнение таких орбит можно получить из выражения эллиптической функции Вейерштрасса через эллиптические функции Якоби (17)

(17)

где   и модуль

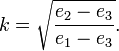
В пределе совпадающих e₂ и e₁, модуль стремится к единице, а w переходит в n(φ-φ₀). Выбирая φ₀ мнимым, равным   (четверть периода), приходим к приведённой выше формуле.

Падение на центр

В действительных решениях  , в которых φ₀ равняется ω₁ или некоторым другим действительным числам, ζ не может стать меньше e₁ из-за уравнений движения 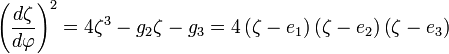(18

(18)

ζ безгранично возрастает, что соответствует падению на центр r = 0 после бесконечного числа оборотов вокруг него.

Вывод уравнения орбит Из уравнения Гамильтона — Якоби

Преимущество этого вывода состоит в том, что он применим и к движению частиц, и к распространению волн, что легко приводит к выражению для отклонения света в гравитационном поле при использовании принципа Ферма. Основная идея состоит в том, что благодаря гравитационному замедлению времени части волнового фронта, которые находятся ближе к гравитирующей массе, двигаются медленнее чем те, которые находятся дальше, что приводит к искривлению распространения волнового фронта.

В силу общей ковариантности уравнение Гамильтона — Якоби для одной частицы в произвольных координатах можно записать в виде (19)

(19)

В метрике Шварцшильда это уравнение примет вид

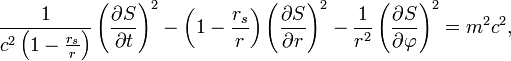
где плоскость отсчёта θ сферической системы координат расположена в плоскости орбиты. Время t и долгота φ — циклические координаты, поэтому решение для функции действия S запишется в виде (20)

(20)

где E и L представляют энергию частицы и её угловой момент, соответственно. Уравнение Гамильтона — Якоби приводит к интегральному решению для радиальной части S_r(r)

Дифференцируя функцию S обычным образом

приходим к уравнению орбиты, полученному ранее

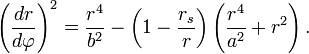
Этот подход можно использовать для элегантного вывода скорости прецессии орбиты.

В пределе нулевой массы m (или, что эквивалентно, бесконечного a), радиальная часть действия S становится равной 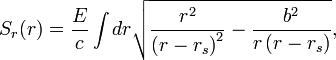(21)

(21)

из этого выражения выводится уравнение для отклонения луча света

.