Приближённая формула для отклонения света

В пределе массы частицы m, стремящейся к нулю (или, эквивалентно,  ), уравнение орбиты переходит в

Разлагая это выражение по степеням отношения r_s/r, в первом приближении получаем отклонение δφ безмассовой частицы при пролёте мимо гравитирующего центра:

Константу b здесь можно интерпретировать как прицельный параметр — расстояние наибольшего приближения. Приближение, использованное при выводе этой формулы, достаточно точное для большинства практических приложений, включая измерениягравитационного линзирования. Для света, проходящего вблизи солнечной поверхности, отклонение составляет около 1,75 угловой секунды.

Связь с классической механикой и прецессия эллиптических орбит

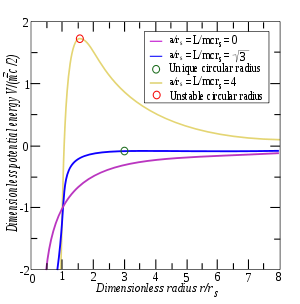
Эффективный потенциал для различных значений момента импульса. При малых r потенциал уменьшается (в отличие от классической задачи Кеплера), позволяя частице падение на центр. Тем не менее, при  родившаяся снаружи частица не может преодолеть потенциальный барьер и избегает захвата. При предельном нормированном угловом моменте   существует метастабильная круговая орбита, обозначенная зелёной окружностью, и есть бесконечно накручивающиеся на неё и скручивающиеся с неё спиральные орбиты. При малых a / r_s частица захватывается и падает на центр.

Уравнения движения частицы в поле Шварцшильда 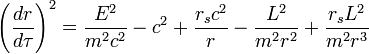(8)

(8)

можно переписать, используя определение гравитационного радиуса r_s:

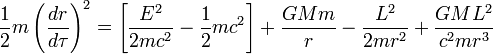
что эквивалентно движению нерелятивистской частицы с энергией   в одномерном эффективном потенциале (9)

Первые два члена соответствуют известным классическим: гравитационному потенциалу притяжения Ньютона и центробежному потенциалу отталкивания, и только третий член не имеет аналога в классической задаче Кеплера. Как показано ниже и в другой статье, такой член приводит к прецессии эллиптических орбит на угол δφ за каждый оборот

где A — большая полуось орбиты, а e — её эксцентриситет.

Третий член имеет характер притяжения и меняет поведение потенциала при малых r — вместо того, чтобы уходить в  , препятствуя падению частицы на центр (как это было в классической задаче Кеплера), потенциал уходит на  , позволяя частице падать (см. подробнее падение в чёрную дыру).

Круговые орбиты и их стабильность

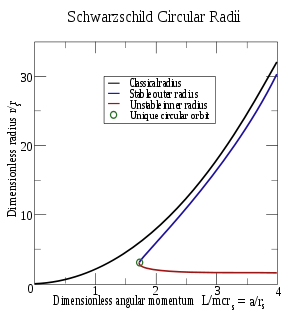
Радиусы стабильных (голубая кривая) и нестабильных (красная кривая) орбит в зависимости от нормированного углового момента a/r_s = L/mcr_s. Графики встречаются в единственной точке (обведённой зелёной окружностью), где  . Для сравнения приведены также радиусы всегда стабильных орбит классической задачи Кеплера (чёрная кривая).

Эффективный потенциал V можно переписать через параметры длины a и b 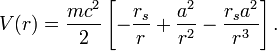(9):

(9)

Круговые орбиты возможны при эффективной силе, равной нулю

т. е. когда две притягивающие силы — Ньютонова гравитация (первый член) и её релятивистская поправка (третий член) — точно сбалансированы отталкивающей центробежной силой (второй член). Существуют два радиуса, на которых достигается эта компенсация,

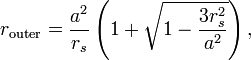
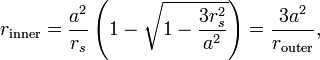
которые прямо выводятся из квадратного уравнения выше. Внутренний радиус r_inner оказывается нестабильным при любых значениях a, так как сила притяжения там растёт быстрее, чем сила отталкивания, поэтому любое возмущение приводит к падению частицы на центр. Орбиты внешнего радиуса стабильны — там релятивистское притяжение невелико, и их характер почти совпадает с траекториями нерелятивистской задачи Кеплера.

Когда a много больше r_s (классический случай), размеры орбит стремятся к

Подставляя определения a и r_s в r_outer, получаем классическую формулу для частицы на круговой орбите вокруг гравитирующего центра массой M

где ω_φ — орбитальная угловая скорость частицы.

Когда a² стремится к 3r_s² (сверху), внешний и внутренний радиусы смыкаются к

Решение квадратного уравнения гарантирует, что r_outer всегда больше 3r_s, а r_inner лежит между ³⁄₂ r_s и 3r_s. Круговые орбиты с радиусом меньше ³⁄₂ r_s невозможны. Сама орбита r_inner = ³⁄₂ r_s является предельным случаем для безмассовых частиц, когда  , поэтому сферу этого радиуса иногда называют фотонной сферой.