Прецессия эллиптических орбит

В нерелятивистской задаче Кеплера частица следует всегда по одному и тому же идеальному эллипсу(красная орбита). Общая теория относительности изменяет силу, действующую на частицу, так что притяжение растёт быстрее, чем в теории Ньютона (в шварцшильдовых координатах). Это возмущение вызывает вращение почти эллиптической орбиты (голубой) — прецессию в направлении вращения планеты; этот эффект надёжно измерен для Меркурия, Венеры и Земли. Жёлтая точка представляет собой центр притяжения, например, Солнце.

Скорость прецессии орбиты можно вывести из эффективного потенциала V. Малое отклонение по радиусу от орбиты-окружности r=r_outer будет осциллировать с частотой (10)

(10)

Разложение в ряд даёт

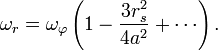
Умножение на период обращения T приводит к прецессии на одном обороте

где ω_φT = 2п и использовано определение a. Подставляя r_s, получаем

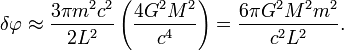
Используя большую полуось орбиты A и эксцентриситет e, связанные соотношением

мы приходим к наиболее известной формуле прецессии (11)

(11)

Точное решение для орбиты в эллиптических функциях

Вводя безразмерную переменную

уравнение для орбиты

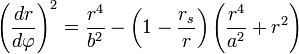
можно привести к упрощённому виду

где постоянные безразмерные коэффициенты g₂ и g₃ определены как

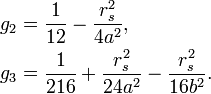
Решение этого уравнения для орбиты задаётся в виде неопределённого интеграла (12)

(12)

Отсюда следует, что с точностью до фазового сдвига,  , где   — эллиптическая функция Вейерштрасса с параметрами g₂ и g₃, и φ₀ — постоянная интегрирования (возможно комплексная).

Качественный характер возможных орбит

Полный качественный анализ возможных орбит в поле Шварцшильда впервые был проведён Ю. Хагихарой в 1931 году.

Траектории в поле Шварцшильда описываются уравнением движения (13)

(13)

Если дискриминант   больше 0, то кубическое уравнение

имеет три различных действительных корня e₁, e₂ и e₃, которые можно упорядочить по убыванию

e₁ > e₂ > e₃.

В таком случае решение   является эллиптической функцией с двумя полупериодами, одним чисто действительным

и вторым — чисто мнимым

Оставшийся промежуточный корень определяет комплексный полупериод ω₂ = -ω₁ - ω₃. Эти величины связаны с соответствующими корнями через уравнения   (i= 1, 2, 3). Следовательно, при   (n — целое число) производная ζ обращается в 0, то есть траектория достигает периастра или апоастра — точки максимального приближения и удаления, соответственно:

так как

Качественный характер орбиты зависит от выбора φ₀. Решения с φ₀ = ω₂ соответствуют либо орбитам, колеблющимся от ζ=e₂ до ζ=e₃, либо траекториям, уходящим на бесконечность (ζ=-1/12). Наоборот, решения с φ₀, равным ω₁ или любому другому действительному числу, описывают орбиты, сходящиеся к центру, так как действительное ζ не может быть меньше e₁ и поэтому будет неотвратимо расти до бесконечности.

Квази -эллиптические орбиты

Решения  , в которых φ₀ = ω₂, дают действительные значения ζ при условии, что энергия E удовлетворяет неравенству E² < m² c⁴. В таком случае ζ принимает значения в интервале e₃ ≤ ζ ≤ e₂. Если оба корня больше -1/12, то ζ не может принять этого значения, соответствующего уходу частицы на бесконечность, поэтому тело будет совершать финитное движение, которое можно представить как движение по прецессирующему эллипсу. Радиальная координата тела будет бесконечно колебаться между (14), (15)

(14)

и

(15)

которые соответствуют экстремальным значениям ζ. Действительный период эллиптической функции Вейерштрасса составляет 2ω₁; таким образом, частица возвращается к тому же радиусу, когда угловая координата возрастает на 2ω₁, что, вообще говоря, отличается от 2π. Поэтому орбита как правило прецессирует, однако при   угол прецессии за один оборот (2ω₁ - 2π) довольно мал.

Стабильные круговые орбиты

Специальный случай 2e₂ = 2e₃ = −e₃ соответствует решению с ζ = const = e₂ = e₃. Получается круговая орбита с r = r_outer, не меньшим 3r_s. Такие орбиты устойчивы, так как малые возмущения параметров приводят к расщеплению корней, приводя к квази-эллиптическим орбитам. Например, если частицу чуть "подтолкнуть" в радиальном направлении, то она станет колебаться около невозмущённого радиуса, описывая прецессирующий эллипс.