22. Понятие и меры вариации

Вариация – колеблемость, многообразие, изменяемость величины признака у единиц совокупности. Измерение вариации позволяет определить степень воздействия на данный признак других варьирующих признаков. Вариация существует в пространстве и во времени. Показатели, характеризующие вариацию: Абсолютные: 1) R (размах вариации) = x_max – x_min; показывает, насколько велико различие между единицами совокупности, имеющими максимальное и минимальное значения. Недостаток: оценивает только границы варьирования признака и не отражает колеблемость признака внутри этих границ; 2) 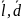(среднее линейной отклонение); отражает все колебания варьирующих признаков и дает обобщающую характеристику степени колеблемости признака в совокупности. 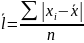- простое; 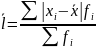– взвешенное; 3) 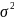(дисперсия) – средний квадрат отклонений значений признака от их средней величины; 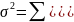– простая, 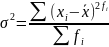- взвешенная; 4) 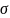(среднее квадратическое отклонение) – обобщающая характеристика размеров вариации признаков совокупности. 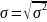. Относительные: 5) V (показатель вариации); V = 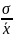∙ 100%. V < 30% → совокупность однородна, V > 30% → совокупность неоднородна. 6) 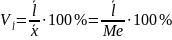(линейный коэффициент вариации)

23. Свойства дисперсии

В вариационном ряду распределения с равными интервалами дисперсию можно рассчитать, используя «способ моментов», который основан на свойствах дисперсии: 1) дисперсия постоянной величины равна нулю; 2) уменьшение всех значений признака на одну и ту же величину А не изменяет дисперсию, следовательно, средний квадрат отклонений можно определить не по заданными значениям признака, а по их отклонениям от какого-либо постоянного числа; 3) уменьшение всех значений признака в k раз уменьшает дисперсию в k² раз, а среднее квадратическое отклонение в k раз, следовательно, все значения признака можно разделить на какое-то постоянное число, определить среднее квадратическое отклонение, а затем умножить его на это постоянное число. 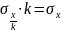. 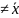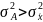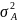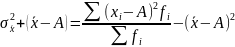4) если вычислить от любой величины А, отличающейся от средней (А ), то будет больше , вычисленной от ( ), следовательно = , т.е. имеет свойство минимальности. Если А=0, то 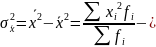. В условиях нормального распределения существует зависимость между величиной и количеством наблюдений:

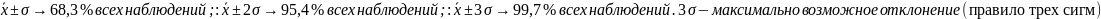
24. Виды дисперсии и правила их сложения.

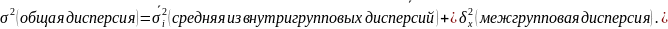
Статистическая совокупность характеризуется признаками: факторными (оказывает влияние) и результативными (зависит от). Для выявления взаимосвязи исходная совокупность делится на 2 или более групп по факторному признаку. Выводы о степени их взаимосвязи основываются на анализе вариаций результативного признака; при это применяется правило сложения дисперсий: 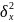отражает ту часть результативного признака, которая обусловлена воздействием факторного признака. Это воздействие проявляется в отклонении групповых средних от общей средней. 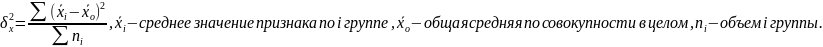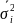отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме тех, по которым осуществлялась группировка. 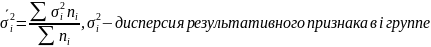. Эмпирическое корреляционное распределение (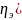 характеризует тесноту связи между факторным и результативным признаками. 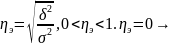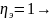группировочный признак не влияет на результативный, результативный признак изменяется только в зависимости от признака, положенного в основании группировки, следовательно, влияние других факторных признаков равно нулю.