17. Сущность средних показателей и исходное соотношение средней.

Средняя величина – обобщенная качественная характеристика признака статистической совокупности конкретных условий места и времени. Показатель в форме средней величины отражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Сущность средней заключается в том, что в ней взаимозаключаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайны факторов, и учитываются изменения, вызванные действием основных факторов (отражает основные факторы, черты, признаки). Средняя величина отражает типичный уровень признака и абстрагируется от индивидуальных особенностей, присущих отдельным единицам. Исходное соотношение средней (ИСС) – логическая форма для расчета величины. ИСС = . Объем осредняемого признака – суммарное значение осредняемого признака. Пример: Расчет возраста: ИСС = 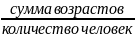. В зависимости от того, в каком виде представлены исходные данные для расчета средней, зависит, каким образом будет реализовано исходное соотношение. Виды средней величины могут быть простыми и взвешенными. 1) Средняя арифметическая; 2) Средняя гармоническая; 3) Средняя геометрическая; 4) Средняя квадратическая/кубическая; 5) Структурные средние величины (мода, медиана)

18. Средние арифметические

Данные несгруппированы – средняя арифметическая простая. = 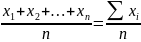. Данные сгруппированы – средняя арифметическая взвешенная. , – частота (сколько раз значение признака встречается в совокупности)

19. Свойства средней арифметической.

Используются для упрощения расчетов: 1) произведение средней на сумму частот = сумма произведений отдельных вариантов на соответствующие им частоты. . 2) сумма отклонений индивидуального значения признака от средней арифм. = 0. . 3) если все осредняемые величины уменьшить/увеличить на постоянное число А, то средняя арифм. соответственно уменьшится/увеличится на А. . 4) Если все варианты значения признака уменьшить/увеличить в k раз, то средняя соответственно уменьшится/увеличится в k раз. . 5) если все частоты (f_i) уменьшить/увеличить в k раз, то средняя не изменится. . 6) сумма квадратов отклонений индивидуального значения признаков от средней арифм. меньше, чем сумма квадрата и отклонений от любой другой произвольной величины С.

20. Средние гармонические – величина, обратная средней арифм. из обратных значений признаков. – простая, – взвешенная. Средние арифм. и средние гармонич. могут применяться в одних и тех же ситуациях, но по разным данным. Не известен числитель → средняя арифм.; не известен знаменатель → средняя гармонич.

21. Другие виды средних величин.

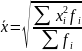1) Средняя геометрическая – применяется в случаях определения средней по значениям, имеющим большой разброс или в случая определения средней по относительным показателям. – простая, – взвешенная. 2) Средняя квадратическая – используется когда вместо индивидуальных значений признака представлены квадраты исходных величин. – простая, – взвешенная. 3) Средняя хронологическая – используется для определения средних значений рядов динамики. Средняя хронологическая простая используется в моментальных рядах с равными промежутками времени (t). , где n – количество дат, в которых известно количество признака. Средняя хронологическая взвешенная используются для определения средней величины в рядах динамики с неравными интервалами времени: 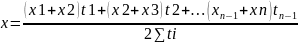, где ti – промежутки времени между иксами. 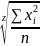5) Средняя степенная: , z = 1 → сред. арифм., z = 0 → сред. геометр., z = -1 → сред. гармонич., z = -2 → сред. квадратич.