
- •1. Метод Данилевского
- •1.1 Метод Гаусса.
- •1.2 Метод Гаусса с выбором главного элемента. ( )
- •1.3 Метод оптимального исключения ( )
- •1.4 Метод прогонки.
- •II. Методы, основанные на разложении матрицы коэффициентов.
- •2.1. Метод квадратного корня (случай эрмитовой матрицы)
- •2.2 Частный случай метода квадратного корня (случай симметричной матрицы)
- •2.3 Схема Халецкого (случай матрицы с отличными от 0 глав. Минорами).
- •Приближенные (итерационные) методы.
- •2.1 Метод простой итерации.
- •2.2 Метод Якоби.
- •2.3 Метод Зейделя.
- •2. Решение полной проблемы собственных чисел.
- •1. Метод Данилевского
- •2. Итерационный метод вращений.
- •Решение нелинейных уравнений.
- •1.2.1 Метод половинного деления (метод дихотомии).
- •1.2.2 Метод Ньютона или метод касательных
- •1) Существование производных 1-го и 2-го порядков;
- •1.2.3 Метод хорд. Метод секущих.
- •1.2.4 Метод простой итерации.
- •III. Решение дифференциальных уравнений.
- •Задачи с начальными условиями для оду (задача Коши).
- •Численные методы решения дифференциальных уравнений Одношаговые методы. Метод Эйлера и его модификации
- •Одношаговые методы. Метод Эйлера и его модификации.
- •1 Метод Эйлера
- •2. Метод Рунге-Кутта.
- •Многошаговые методы
- •1. Формулировка методов
- •Постановка линейных краевых задач для оду 2-го порядка.
- •Конечно-разностный метод решения краевой задачи.
2.2 Метод Якоби.
Пусть матрица
![]() системы (1) представлена в виде
системы (1) представлена в виде
![]() ,
,
где
![]() – диагональная, а
– диагональная, а
![]() и
и
![]() – соответственно левая и правая строго
треугольные (т.е. с нулевой диагональю)
матрицы. Тогда система (1) может быть
записана в виде
– соответственно левая и правая строго
треугольные (т.е. с нулевой диагональю)
матрицы. Тогда система (1) может быть
записана в виде
![]() , (11)
, (11)
и, если на диагонали исходной матрицы нет нулей, то эквивалентной (1) задачей вида (2) будет
![]() ,
,
т.е. в равенствах (2) и (3) следует положить
![]() .
.
Основанный на таком приведении системы (1) к виду (2) метод простой итерации (3) называют методом Якоби:
![]() (12)
(12)
Обратной
матрицей к матрице
![]() служит диагональная матрица
служит диагональная матрица
![]() с элементами диагонали
с элементами диагонали
![]() .
Метод Якоби решения системы (1) в
координатной форме имеет вид
.
Метод Якоби решения системы (1) в
координатной форме имеет вид

Теорема 3. (Достаточный признак сходимости). В случае диагонального преобладания в матрице системы (1) метод Якоби (12) сходится.
Диагональное преобладание в матрице означает, что
 .
(13)
.
(13)
2.3 Метод Зейделя.
Под
методом Зейделя (МЗ) обычно понимается
такой вариант МПИ (3) решения СЛАУ,
приведенной к виду (2), при котором для
подсчета (k+1)-го
приближения неизвестного
![]() при
при
![]() используются уже вычисленные ранее
(k+1)-е
приближения неизвестных
используются уже вычисленные ранее
(k+1)-е
приближения неизвестных
![]() ,
,
![]() ,…
,…![]() .
Таким образом, для системы (2) расчеты
ведутся по формулам
.
Таким образом, для системы (2) расчеты
ведутся по формулам
 (14)
(14)
или
![]()
Если преобразование системы (1) к виду (2) основано на представлении (11) (метод Якоби) , то соответствующие расчетные формулы имеют вид
 (15)
(15)
где
![]() ;
;
![]() – заданное начальное приближение.
– заданное начальное приближение.
Теорема 5. Если матрица системы (1) имеет диагональное преобладание, то метод Зейделя (15) сходится, причем быстрее, чем метод Якоби.
Замечание. В соответствии с теоремой 5 в МЗ (15) в указанных условиях допустимо использование оценок погрешности метода Якоби. Естественно, они заведомо грубее.
Наряду с рассмотренными применяют и другие способы приведения системы (1) к виду (2) для ее решения методом Зейделя.
2. Решение полной проблемы собственных чисел.
1. Метод Данилевского
Сведение
матрицы
![]() преобразованием подобия к
канонической форме Фробениуса Ф:
преобразованием подобия к
канонической форме Фробениуса Ф:

Преобразование
![]() матриц
матриц
![]() и
с помощью невырожденной матрицы
и
с помощью невырожденной матрицы
![]() называется преобразованием подобия.
называется преобразованием подобия.
По
первой строке полученной матрицы
![]() составляется собственный многочлен
:
составляется собственный многочлен
:
![]() .
.
Собственные векторы матрицы
![]()
Умножая
на собственный вектор
![]() ,
получим для собственного вектора
,
получим для собственного вектора
![]() матрицы А
выражение
матрицы А
выражение
![]()
2. Итерационный метод вращений.
Идея в преобразовании матриц к диагональной форме
Любую симметричную действительную матрицу можно привести к диагональному виду преобразованием подобия
![]() , (1)
, (1)
где
![]() – ортогональная матрица (
– ортогональная матрица (![]() )
и
)
и
![]() – диагональная, элементами которой
являются собственные значения
– диагональная, элементами которой
являются собственные значения
![]() матрицы
.
Так как для ортогональной матрицы
обратная совпадает с транспонированной
(
матрицы
.
Так как для ортогональной матрицы
обратная совпадает с транспонированной
(![]() ),
то (1) равносильно
),
то (1) равносильно
![]() (2)
(2)
Метод
вращений
обладает быстрой сходимостью–
это
итерационный процесс, где на каждом
шаге осуществляется такое преобразование
подобия, что
![]() – наибольший недиагональный элемент
по абсолютной величине обращается в 0.
В качестве
– наибольший недиагональный элемент
по абсолютной величине обращается в 0.
В качестве
![]() выбирается матрица вращения. Т.к. матрица
симметричная, то достаточно рассмотреть
элементы выше главной диагонали.
выбирается матрица вращения. Т.к. матрица
симметричная, то достаточно рассмотреть
элементы выше главной диагонали.
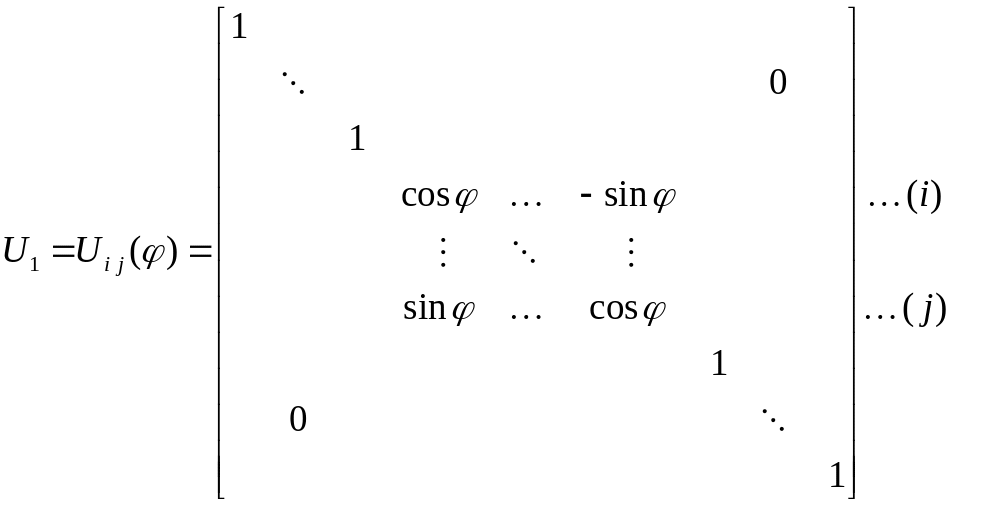 (3)
(3)
Опред.
Вещественные матрицы, отличающиеся от
единичной матрицы, четырьмя элементами,
расположенными на пересечении строк и
столбцов с номерами
![]() и имеющими вид (3) называются матрицами
вращения, в
которой угол
и имеющими вид (3) называются матрицами
вращения, в
которой угол
![]() определяется из условия , что наибольший
недиагональный элемент после преобразования
подобия =0
определяется из условия , что наибольший
недиагональный элемент после преобразования
подобия =0
