Плотность, коэффициент теплопроводности, теплоемкость и коэффициент температуропроводности при нормальных условиях

Вещество	, кг/м3	, Вт/м∙K	С, кДж/кг∙K	a∙106, м2/с
Окись углерода Воздух (сухой) Азот Кислород Латунь Олово Алюминий Медь Вода	1,25 1,293 1,25 1,429 8600 7230 2670 8800 999,9	0,0233 0,0244 0,0243 0,0247 85 64 204 384 0,5513	1,039 1,005 1,03 0,915 0,377 0,221 0,921 0,381 4,212	17,9 18,8 18,9 18,9 33,8 41,1 86,7 112,5 0,131

При выводе уравнений (4.5.10–4.5.11) предполагалось, что поток тепла распространяется в одном направлении (вдоль оси X). Нетрудно обобщить эти уравнения на случай, когда температура в веществе изменяется в трех направлениях и зависит от времени, т. е. является функцией .

Для этого в веществе выделим элементарный параллелепипед с объемом dV = dx dy dz (рис. 62).

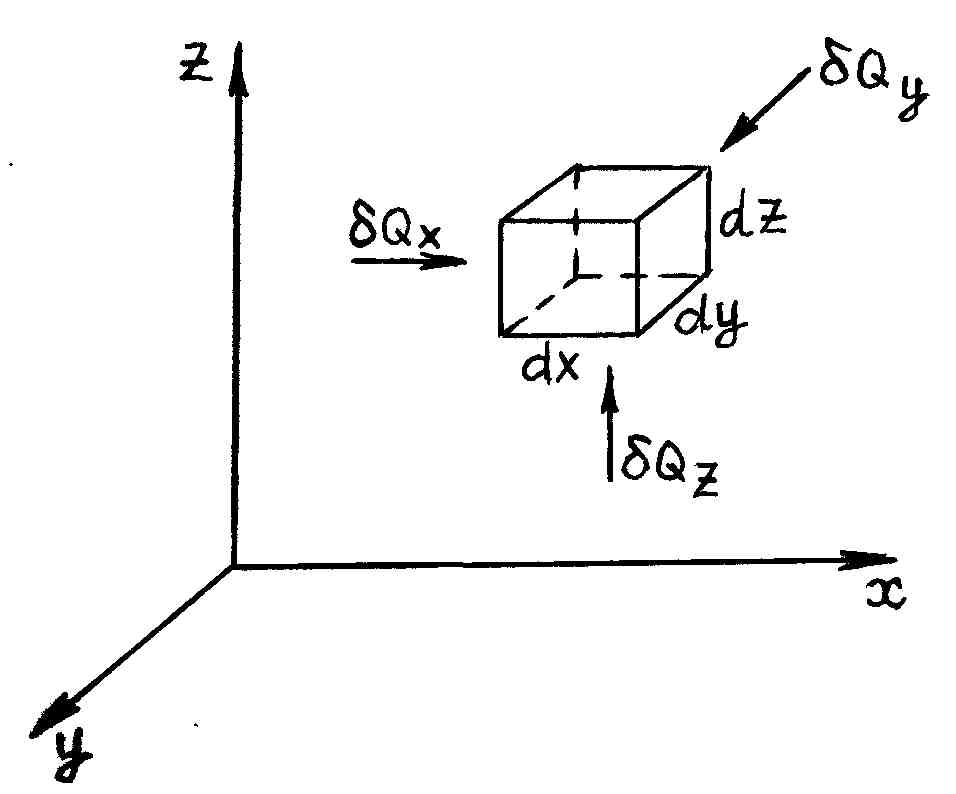
Р и с. 62

В этом случае температуры граней различны, поэтому теплота в параллелепипеде будет распространяться в направлении осей X, Y и Z.

Согласно закону Ж. Фурье (4.5.1), через грань dydz за время dt в объем dV втекает в направлении оси X количество теплоты

, (4.5.12)

через противоположную грань из того же объема dV вытекает в том же направлении количество теплоты

(4.5.13)

где – температура второй грани, а величина определяет приращение температуры в направлении оси X.

Так как макроскопическая работа не совершается, то приращение внутренней энергии вещества, находящегося в параллелепипеде, из-за движения теплоты в направлении оси X будет равно

. (4.5.14)

Совершенно аналогично приращения внутренней энергии в параллелепипеде в направлении осей X и Y представятся в виде

, (4.5.15)

. (4.5.16)

Суммарное приращение внутренней энергии вещества, находящегося в параллелепипеде, за время dt равно

. (4.5.17)

С другой стороны, согласно закону сохранения энергии, количество тепла, поступившего в параллелепипед, идет на приращение внутренней энергии вещества и, как следствие, на повышение его температуры:

, (4.5.18)

где – масса вещества в параллелепипеде, – удельная теплоемкость при постоянном объеме, – приращение температуры во времени (за время dt).

Так как левые части выражений (4.5.17) и (4.5.18) равны, то и правые равны, т. е.

, (4.5.19)

где .

При выводе уравнения теплопроводности (4.5.19) предполагалось, что в произвольно выбранном элементарном параллелепипеде отсутствуют внутренние источники тепла. При наличии таких источников, необходимо к правой части уравнения (4.5.19) добавить величину q_V, равную количеству тепла, поставляемого источниками в единицу объема вещества в единицу времени, разделенную на . Поэтому дифференциальное уравнение теплопроводности с источниками тепла внутри тела будет иметь вид

. (4.5.20)

По существующей классификации дифференциальных уравнений с частными производными второго порядка уравнение теплопроводности является уравнением параболического типа (содержат первую производную по времени). Для решения этих уравнений необходимо располагать начальными и граничными условиями. Начальные условия предполагают, что в начальный момент t = 0 задано распределение температур в теле, т. е. задана функция при t = 0. Граничные условия предполагают задание распределения температур на поверхности тела в любой момент времени. Кроме того, должны быть известны геометрическая форма и размеры тела, а также физические параметры окружающей среды и тела. Все эти условия называют краевыми. Решением уравнения теплопроводности с заданными краевыми условиями является функция , которая определяет температурное поле во всем объеме тела для любого момента времени. Решение большинства реальных задач находят численными методами с использованием вычислительных машин.

В качестве примера рассмотрим простейший, но широко распространенный случай – теплопроводность через однослойную плоскую стенку, длина и ширина которой велики по сравнению с толщиной d (рис. 63).

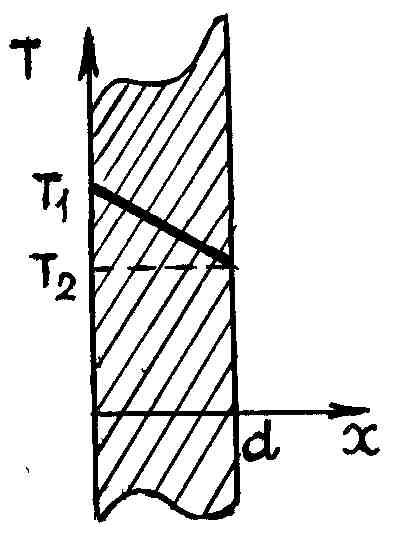
Р и с. 63

Это может быть бетонная или кирпичная стена, отделяющая помещение, в котором поддерживается постоянная температура T₁, от внешней среды, находящейся при другой температуре T₂. Температура изменяется только в направлении, перпендикулярном к плоскости стенки, которое примем за ось X. При стационарном (установившемся) тепловом режиме температура в любой плоскости, параллельной внешним плоскостям стенки и проходящей через любую внутреннюю точку стенки, постоянна и не зависит от времени, т. е. . Так как в направлении осей Y и Z температура не меняется, то . При таких условиях уравнение теплопроводности (4.5.19) принимает вид:

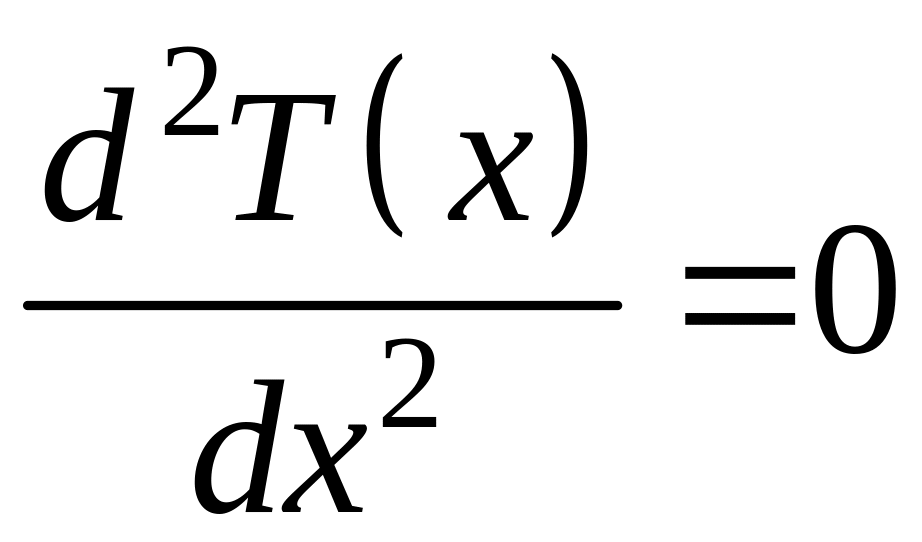. (4.5.21)

Откуда находим

.

Второе интегрирование дает

. (4.5.22)

Постоянные A и B могут быть найдены из граничных условий. При x = 0 T(0) = T₁ = B; при x = d T(d) = Ad + T₁ = T₂ и, таким образом, A = (T₂ –T₁)/d.

Подставив найденные постоянные коэффициенты в уравнение прямой (4.5.22), получим

. (4.5.23)

Плотность теплового потока q найдем по формуле (4.5.3):

. (4.5.24)

Следует заметить, что тепловой поток зависит не от абсолютного значения температур, а от их разности.

Количество тепла, проходящее через площадь S стенки за время t, на основании формулы (4.5.1), равно:

. (4.5.25)

Это количество теплоты прямо пропорционально коэффициенту теплопроводности стенки, ее площади S, промежутку времени t, разности температур на внешних сторонах стенки и обратно пропорционально толщине стенки d.