
- •Глава 4. Физическая кинетика
- •4.1. Средняя длина свободного пробега
- •4.2. Распределение длин свободного пробега молекул
- •4.3. Рассеяние молекулярного пучка в газе. Экспериментальное определение средней длины свободного пробега
- •4.4. Общее уравнение явлений переноса
- •4.5. Теплопроводность. Уравнение теплопроводности
- •Плотность, коэффициент теплопроводности, теплоемкость и коэффициент температуропроводности при нормальных условиях
- •4.6. Вычисление и опытное определение коэффициента теплопроводности
- •4.7. Внутреннее трение (вязкость) газов
- •4.8. Диффузия в газах
- •4.9. Некоторые свойства разреженных газов
4.5. Теплопроводность. Уравнение теплопроводности
Явление теплопроводности наблюдается всегда, если в веществе имеется разность температур, обусловленная какими-либо внешними причинами. С макроскопической точки зрения явление теплопроводности заключается в переносе тепла от горячего слоя к холодному и продолжающемуся до тех пор, пока температура во всем теле не выровняется. В молекулярно-кинетической же теории процесс теплопроводности объясняется тем, что молекулы из горячего слоя, где они имеют большую среднюю кинетическую энергию, проникая в холодную область, передают при столкновениях молекулам этой области часть их кинетической энергии.
Пусть изменение температуры вещества происходит вдоль оси X, в то время как в плоскости, перпендикулярной этой оси, температура постоянна. Опытным путем Ж. Фурье установил закон, согласно которому количество тепла, переносимое за время dt через площадку dS, перпендикулярную оси X, пропорционально величине площадки, времени переноса и градиенту dT/dx температуры:
![]() , (4.5.1)
, (4.5.1)
где
![]() – коэффициент теплопроводности, который,
как видно из закона Ж. Фурье, имеет в
системе СИ размерность Дж/(м∙с∙K)
= Вт/(м∙K), и численно равен
количеству тепла, переносимого в единицу
времени через единичную площадку при
градиенте температуры, равном единице.
Знак “минус” означает, что тепло
переносится от мест более горячих к
более холодным.
– коэффициент теплопроводности, который,
как видно из закона Ж. Фурье, имеет в
системе СИ размерность Дж/(м∙с∙K)
= Вт/(м∙K), и численно равен
количеству тепла, переносимого в единицу
времени через единичную площадку при
градиенте температуры, равном единице.
Знак “минус” означает, что тепло
переносится от мест более горячих к
более холодным.
Закон Ж. Фурье справедлив для веществ, находящихся в любых агрегатных состояниях.
Введем в рассмотрение плотность потока тепла
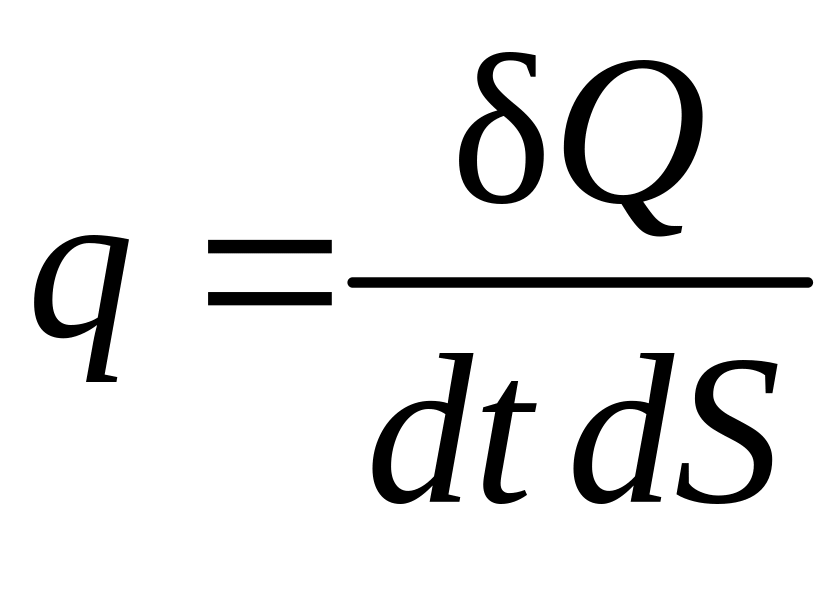 , (4.5.2)
, (4.5.2)
т. е. величина q равна количеству тепла, проходимого через единичную площадку в единицу времени. С учетом (4.5.2) закон Фурье примет вид
![]() . (4.5.3)
. (4.5.3)
Если нагреть некоторую часть тела, то начнется необратимый процесс теплопроводности. При этом, если зафиксировать координату x в теле, то температура в этой точке будет, очевидно, изменяться со временем, достигая, в конце концов, равновесной температуры. Поэтому температура T является не только функцией координаты x, но и времени t, т. е.
T = T(x, t). Тогда, как видно из (4.5.3), поток q будет зависеть от x и t, т. е. q = q(x, t). Процесс теплопроводности, при котором температура и поток являются функциями времени, называется нестационарным.
Выделим в теле, где происходит одномерный (вдоль оси X) нестационарный процесс теплопроводности, элементарный параллелепипед с площадью основания dS и высотой dx (рис. 61).
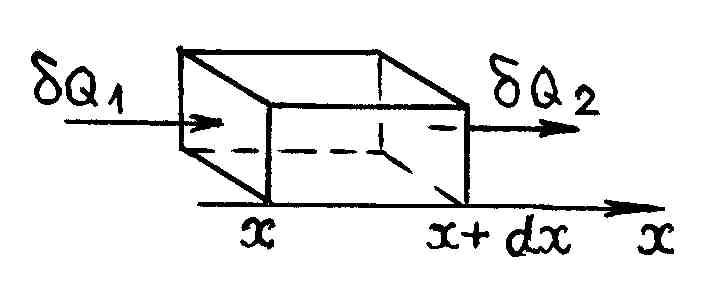
Р и с. 61
Количество тепла, входящее в параллелепипед за время dt через основание с координатой x,
![]() , (4.5.4)
, (4.5.4)
а уходящее через основание с координатой x+dx за то же время
![]() . (4.5.5)
. (4.5.5)
Таким образом, тепло, поступившее в параллелепипед за время dt,
![]() . (4.5.6)
. (4.5.6)
С другой стороны это тепло можно выразить через теплоемкость тела:
![]() , (4.5.7)
, (4.5.7)
где dm и dT
– масса и приращение температуры
вещества, заключенного в параллелепипеде,
соответственно;
![]() и
и
![]() – удельная теплоемкость и плотность
вещества.
– удельная теплоемкость и плотность
вещества.
Разложим функцию q(x+dx, t) в ряд по степеням dx в точке x:
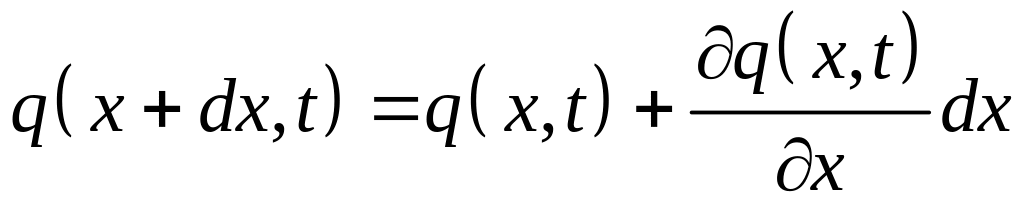 . (4.5.8)
. (4.5.8)
Из выражений (4.5.6–4.5.8) находим
 . (4.5.9)
. (4.5.9)
Подставляя в последнее уравнение вместо q(x, t) его выражение (4.5.3), получим
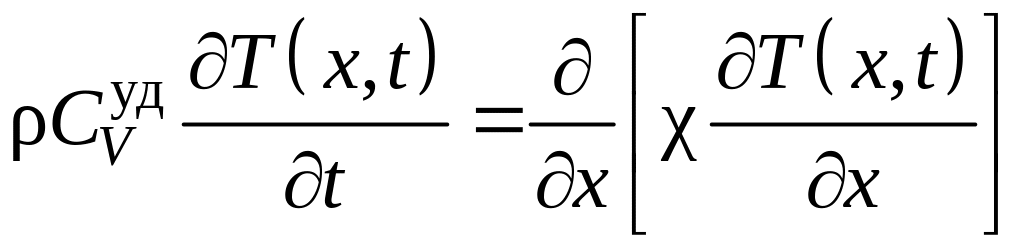 . (4.5.10)
. (4.5.10)
Если коэффициент теплопроводности не зависит от x (однородное вещество), то уравнение (4.5.10) примет вид:
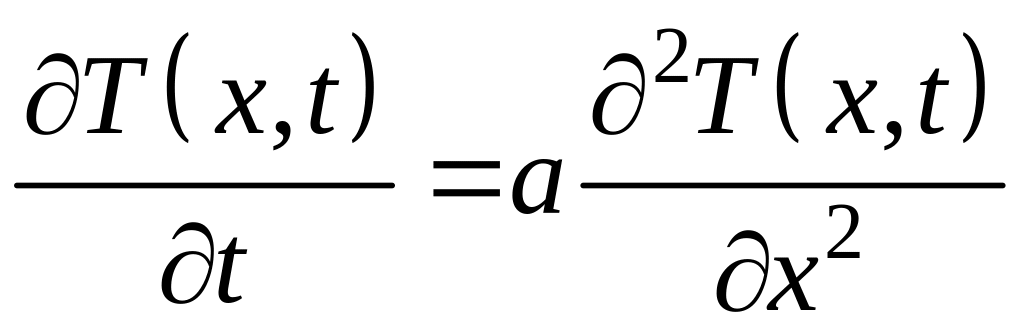 . (4.5.11)
. (4.5.11)
где
![]() –
коэффициент температуропроводности.
–
коэффициент температуропроводности.
Уравнения (4.5.10–4.5.11) носят название дифференциальных уравнений теплопроводности Ж. Фурье. Искомой функцией в этих уравнениях является распределение температуры T(x, t) по пространству и во времени.
Коэффициент температуропроводности a
является физическим параметром вещества
и имеет размерность
![]() .
В нестационарных тепловых процессах
коэффициент a
характеризует скорость изменения
температуры. Если коэффициент
теплопроводности
характеризует способность вещества
проводить теплоту, то коэффициент
температуропроводности a
есть мера теплоинерционных свойств
вещества. В самом деле, из уравнения
(4.5.11) следует, что изменение температуры
в единицу времени
.
В нестационарных тепловых процессах
коэффициент a
характеризует скорость изменения
температуры. Если коэффициент
теплопроводности
характеризует способность вещества
проводить теплоту, то коэффициент
температуропроводности a
есть мера теплоинерционных свойств
вещества. В самом деле, из уравнения
(4.5.11) следует, что изменение температуры
в единицу времени
![]() для любой точки вещества пропорционально
величине a. Поэтому
при прочих одинаковых условиях быстрее
увеличивается температура у того
вещества, которое имеет больший
коэффициент температуропроводности.
Сама же величина a тем
больше, чем больше тепла способно
пропустить вещество в единицу времени
через единичную площадку при единичном
градиенте температуры (т. е. чем больше
)
и чем меньше плотность и теплоемкость
вещества. Из опыта известно (см. табл.
4.5.1), что газы имеют малый, а металлы
большой коэффициент температуропроводности.
Однако для тех и других веществ он
является весьма малой величиной, что
свидетельствует о медленности процесса
теплопроводности.
для любой точки вещества пропорционально
величине a. Поэтому
при прочих одинаковых условиях быстрее
увеличивается температура у того
вещества, которое имеет больший
коэффициент температуропроводности.
Сама же величина a тем
больше, чем больше тепла способно
пропустить вещество в единицу времени
через единичную площадку при единичном
градиенте температуры (т. е. чем больше
)
и чем меньше плотность и теплоемкость
вещества. Из опыта известно (см. табл.
4.5.1), что газы имеют малый, а металлы
большой коэффициент температуропроводности.
Однако для тех и других веществ он
является весьма малой величиной, что
свидетельствует о медленности процесса
теплопроводности.
Таблица 4.5.1
