4.4. Общее уравнение явлений переноса

Равновесное состояние газа в молекулярно-кинетической теории рассматривается как состояние полной хаотичности движения молекул, распределение которых по скоростям подчиняется закону Максвелла. Любое неравновесное состояние газа всегда связано с нарушением полной хаотичности движения молекул и отклонениями от максвелловского распределения их по скоростям. Именно отклонениями от закона Максвелла объясняется направленный перенос энергии, импульса и массы в газах. В каждом конкретном случае внешнего воздействия на газ, выведшего его из равновесия, необходимо найти распределение, заменяющее максвелловское, и лишь затем можно перейти к изучению закономерностей явлений переноса, вызываемого этим воздействием. Этот строгий путь исследования явлений переноса приводит к значительным математическим трудностям, которые до конца не преодолены до сих пор. Поэтому мы рассмотрим только основные закономерности явлений переноса и их приближенное качественное обоснование.

Ввиду хаотичности теплового движения молекул приближенно можно считать, что молекулы движутся только вдоль трех взаимно перпендикулярных осей. При этом вдоль каждой оси движется 1/3 всех молекул газа. Движение молекул вдоль каждой оси в обоих направлениях равновероятно. Поэтому в положительном направлении каждой из осей движется 1/6 часть общего числа молекул. Будем также считать, что все молекулы имеют одну и ту же скорость, равную их средней скорости .

Выберем площадку dS, расположенную перпендикулярно оси X. Тогда число частиц, проходящих через эту площадку за время dt

, (4.4.1)

где n – число частиц в единице объема.

В явлениях переноса каждая молекула при своем хаотическом движении переносит некоторую физическую величину. В случае теплопроводности переносимой величиной является кинетическая энергия молекулы, которая переносится оттуда, где она больше (выше температура), туда, где она меньше (ниже температура), в случае вязкого трения молекула переносит импульс, т. е. величину, равную произведению массы молекулы на гидродинамическую скорость направленного движения слоя газа или жидкости, и, наконец, в явлении диффузии переносимой величиной служит концентрация диффундирующей компоненты, рассчитанная на одну молекулу.

Будем считать, что переносимая величина , отнесенная к одной молекуле, изменяется только в направлении оси X. Значение этой величины изменяется при столкновениях молекул и сохраняется постоянной между соударениями, т. е. на длине свободного пробега . Расположим площадку dS, перпендикулярно оси X, в точке x (рис. 60).

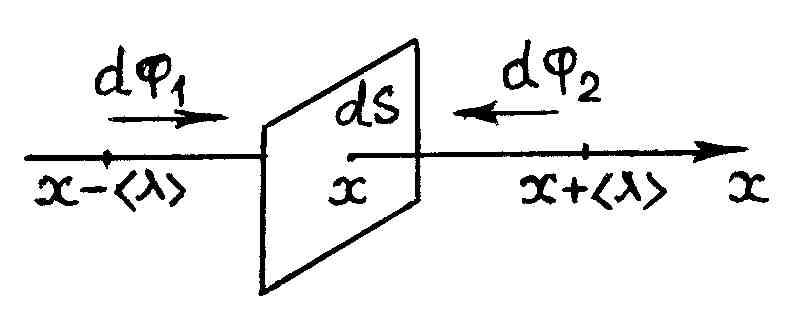
Р и с. 60

Молекулы, пересекающие выделенную площадку слева направо, переносят через нее то значение величины , которое они имели после последнего столкновения перед площадкой, т. е. . Поток этой величины, согласно (4.4.1)

. (4.4.2)

Аналогично, поток величины справа налево

. (4.4.3)

Результирующий поток в направлении оси X

. (4.4.4)

Если бы переносимая величина была постоянна по всему объему, занимаемому газом (равновесие), то потоки этой величины через площадку слева направо и справа налево были бы одинаковы, и результирующий поток был бы равен нулю. Поэтому, чтобы выявить сущность явлений переноса, берется разность соответствующих потоков, которая определяет поток в направлении оси X.

Разложим функции , стоящие в квадратной скобке выражения (4.4.4), в ряд по степеням малой величины в точке x:

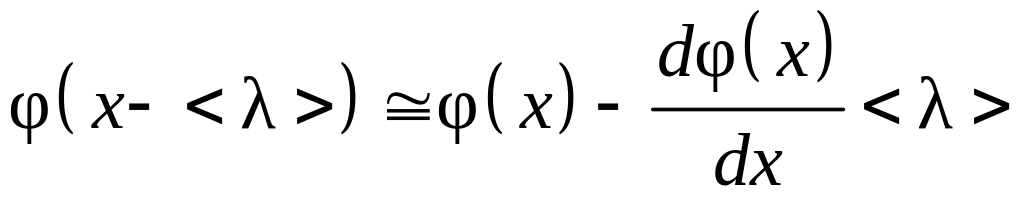, (4.4.5)

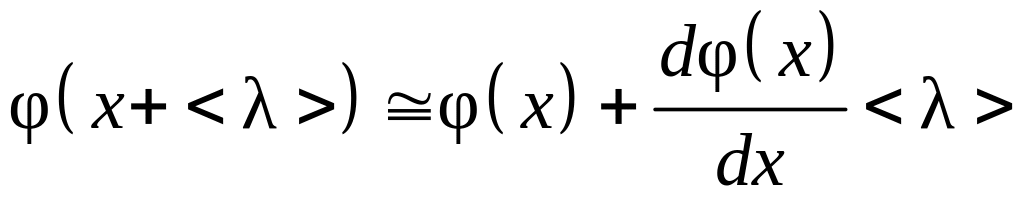. (4.4.6)

Подставим разложения (4.4.5–4.4.6) в (4.4.4). В результате будем иметь

. (4.4.7)

Соотношение (4.4.7) является общим уравнением переноса физической величины и имеет такой же вид, как и в строгой теории, кроме множителя 1/3, который в строгой теории имеет значение близкое к 1/3.