31. Несобственные интегралы с бесконечными пределами интегрирования от неотрицательных функций. Доказать признаки сравнения. Эталонные функции. Примеры.

Пусть подынтегральная функция тогда является возрастающей функцией.

Таким образом у функции имеется две возможности:

1) т.е. возрастает неограниченно;

2) т.е. ограничена сверху.

В этом случае по теореме о пределе монотонной переменной мы имеем, что существует предел и он не превосходит M, т.е.

Т.е. в этом случае несобственный интеграл сходится.

Таким образом для неотрицательных функций исключается возможность отсутствия пределов у . Это позволяет построить хорошую теорию исследования этих интегралов. Основной способ исследования на сходимость несобственных интегралов заключается в сравнении их с уже известными интегралами, иначе говоря с интегралами от так называемых эталонных функций.

Теорема 1. (признак сравнения в обычной форме).

Пусть функции и не отрицательны интегрируемые и справедливо соотношение

для

Тогда если сходится, то сходится . Если расходится, то тоже расходится.

Доказательство.

Проинтегрируем исходное неравенство в пределах от a до N, получим

Если то J_N ограничена сверху, а значит по теореме о пределе монотонной переменной т.е. интеграл сходится.

Обратное утверждение доказывается совершенно аналогично.

Гораздо чаще, чем теорема 1, на практике применяется теорема 2 (признак сравнения в предельной форме)

Пусть функции и неотрицательны и интегрируемые и пусть

при этом

Тогда и сходятся и расходятся одновременно.

Доказательство.

По теореме о связи последовательности, имеющей предел с бесконечно малой, мы имеем где БМ. Иначе говоря, для достаточно больших N справедливо соотношение

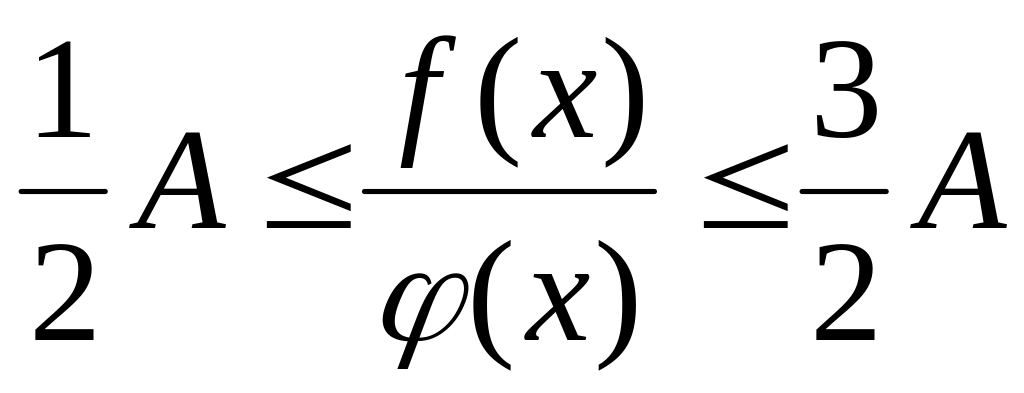
А теперь воспользуемся теоремой 1.

Для определения теорем сравнения нужно иметь набор эталонных функций, т.е. функции, о которых заранее известно сходятся или расходятся интегралы от них. В качестве таких функций чаще всего выбираются такие степенные функции

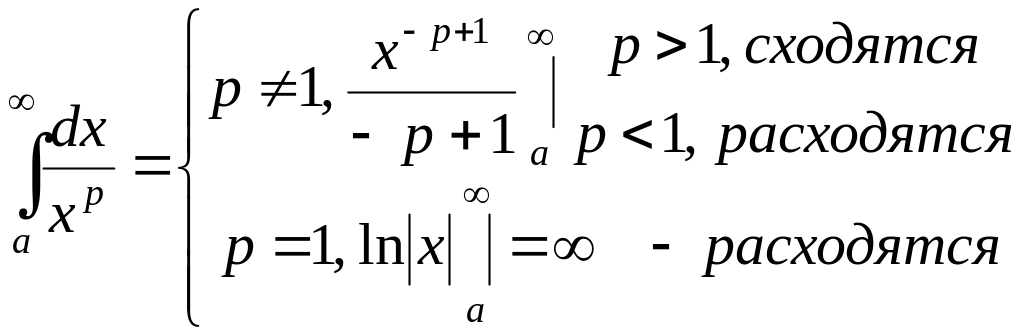
32.Дать определения абсолютной и условной сходимости несобственных интегралов. Доказать теорему о связи сходимости к абсолютной сходимости. Примеры.

Если подынтегральная функция имеет произвольный знак, то - немонотонная функция и поэтому вся предыдущая теория не годится. Однако, имеется один частный, но важный случай, когда можно сказать что-то определенное и об этих интегралах. Это случай абсолютной сходимости.

Говорят, что сходится абсолютно, если сходится

Теорема 3. Если интеграл сходится абсолютно, то он сходится.

Однако, возможна ситуация, когда интеграл от модуля расходится, а исходный интеграл сходится. В этом случае

- расходится; - сходится условно.

33.Дать определение несобственных интегралов от неограниченных функций. Сформулировать их свойства, теоремы сравнения для них. Привести эталонные функции. Примеры.

Пусть функция f(x) определена на [a;b) и

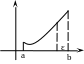
В этом случае опять нельзя определить интеграл обычным образом с помощью интегральных сумм, т.к. в последнем слагаемом поэтому опять обрезают хвост и определяем несобственный интеграл от неограниченной функции, как предел собственных интегралов при , т.е.

Если этот предел существует и конечен, то несобственный интеграл сходится. Если же он не существует или равен , то несобственный интеграл расходится.

Все свойства несобственных интегралов 1-ого рода сохраняются и для несобственных интегралов 2-ого рода. Более того, если существует то сохраняется и формула Ньютона-Лейбница

Замечание. Если точка разрыва 2-ого рода подынтегральной функции находится внутри области интегрирования, то мы вырезаем ее окрестность и получаем 2 несобственных интеграла 2-ого рода, при этом окрестности вырезаются вообще говоря не симметрично.

Для несобственных интегралов 2-ого рода от положительных функций также справедливы теоремы сравнения. Однако, в качестве эталонных функций выбираются функции