1.Фактори, що впливають на надійність технічних об’єктів.

Експоненціальний розподіл ймовірності безвідмовної роботи. Інтенсивність відмов.

1. Експоненціальний та інші розподіли ймовірності безвідмовної роботи

На рис. 1.4 показана типова крива, що характерна для електронних приладів та їх компонентів. Можна стверджувати (про це свідчить статистика), що саме для цього класу об’єктів інтенсивність відмов тривалий час залишається практично постійною, тобто . Тривалість цього періоду для більшості електронних компонентів (ІС, транзисторів, конденсаторів, діодів, резисторів, тощо) вимірюється роками, тому є всі підстави вважати, що за реальні періоди експлуатації електронного обладнання суттєвої деградації і старіння компонентів не відбувається. Наприклад, дослідження на фізичному рівні методом електронної мікроскопії транзисторів свідчать, що навіть за 20-30 років жодних помітних змін у структурі p-n переходів не вдається зафіксувати.

Однак зразу треба застерегти, що ця властивість характерна лише для “чисто” електронних компонентів і не може бути віднесена до елементів обладнання електромеханічного типу (реле, потенціометри, роз’єми) та електронновакуумних приладів (кінескопи, індикатори, тощо).

Зауважимо, до речі, що в цілому будь-яка формула, зокрема і , є лише математичною моделлю фізичного (хімічного) процесу, що відбувається насправді у внутрішній структурі того, чи іншого елементу обладнання. І, тільки з’ясувавши закономірності цього процесу, можна отримати більш точні співвідношення для визначення часу, поки об’єкт буде залишатися працездатним. Ці співвідношення повинні носити фізичний (хімічний) характер і описувати реальні процеси, а не поведінку моделі. Так, наприклад, для лампочок розжарення такі процеси досить детально вивчені: вольфрамова спіраль з часом поступово випаровується, стає більш тонкою, з’являються неоднорідності по товщині. Коли товщина досягає критичної величини, лампочка перегорає. Цей процес має визначений характер, і можна досить достовірно прогнозувати середній час напрацювання лампочок певного виробника до відмови. (Підкреслимо, лише середній час, тому що кожна лампочка має деякі відхилення своїх параметрів від середніх значень).

Але повернемося до електронних виробів, для яких , тобто

, або

.

Розв’язавши це диференціальне рівняння відносно , отримаємо

(1.3)

Таким чином, за умови ймовірність безвідмовної роботи об’єкту описується експоненціальним законом розподілу, тобто зменшується з часом як експонента.

Експоненціальний розподіл в теорії ймовірності є одним із найпростіших. Він повністю визначається лише одним параметром і дозволяє отримати прості співвідношення для середнього часу (математичного сподівання) безвідмовної роботи об’єкта

(1.4)

– це, так зване, напрацювання на відмову, або очікуваний час між відмовами.

Слід зазначити, що цей параметр не слід сприймати (за назвою) дослівно, тому що ймовірність пропрацювати такий час без відмов досить мала. Дійсно,

.

Напрацювання на відмову – це лише формальний параметр, який має таку назву, що за змістом відповідає дійсності тільки для об’єктів, які після відмови зразу ж відновлюються (ремонтуються).

Цікавою є і така властивість експоненціального розподілу. Визначимо ймовірність безвідмовної роботи пристрою за час у інтервалі . Відповідно з (1.1) отримаємо

, (1.5)

звідки витікає, що ймовірність безвідмовної роботи залежить тільки від тривалості періоду експлуатації пристрою і не залежить від того, скільки пристрій пропрацював до цього. Тобто об’єкт, для якого чинний експоненціальний розподіл, залишається весь час мовби новим. Це, до речі, означає, що, наприклад, між ІС, випаяною із пристрою, що деякий час пропрацював, і новою, яку ми взяли із упакування, з точки зору надійності немає жодної різниці. Можна вважати, що більшість електронних компонентів за реальний час експлуатації (кілька років) не старіє, тобто деградаційні процеси, які в них відбуваються, настільки незначні і непомітні, що їх можна не враховувати.

Ще одна властивість експоненціального розподілу, яка суттєво спрощує розрахунок надійності складних систем, полягає у наступному. Розглянемо, наприклад, комп’ютерну мережу, що складається із ПК. За призначенням і умовами експлуатації мережа вважається працездатною лише тоді, коли всі її компоненти працездатні. Таке з’єднання компонентів називають послідовним з точки зору надійності (електрично таке з’єднання не обов’язково є послідовним). Тоді ймовірність безвідмовної роботи мережі є добутком ймовірностей безвідмовної роботи компонентів, тобто

,

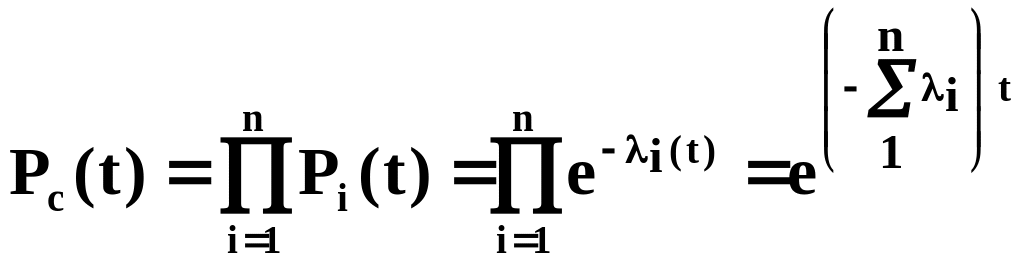або , (1.6)

де - відповідно ймовірність безвідмовної роботи кожного ПК та інтенсивність відмов; - відповідні параметри системи (мережі) із комп’ютерів.

Це означає, що коли всі компоненти системи є необхідними для забезпечення її працездатності, то інтенсивність відмов системи є сумою інтенсивностей відмов компонентів.

Таке просте правило є дуже зручним інструментом для розрахунку надійності складних систем. Але тут необхідно застерегти, що воно є чинним лише для компонентів, для яких . В інших випадках розрахунки суттєво ускладнюються через залежність інтенсивності відмов від часу. Тому залишається справедливою лише формула

,

а відповідний розподіл можна знайти, обчисливши значення для ряду значень часу.

Зрозуміло, що далеко не всі компоненти, які застосовуються в приладобудуванні, радіотехніці, телекомунікаційних мережах тощо мають постійну інтенсивність відмов. Тому, на жаль, обмежитись використанням тільки експоненціального закону не можна. Для компонентів, в яких відбуваються помітні процеси старіння (механічні, електромеханічні, гумотехнічні, тощо) застосовуються інші розподіли. Серед таких розподілів найбільш універсальним є нормальний розподіл (Гауса), для якого густина розподілу

(1.7)

і функція розподілу, тобто ймовірність того, що об’єкт відмовить за час, менший, ніж , є площа під відповідною ділянкою кривої розподілу

. (1.8)

Нормальний розподіл визначається двома параметрами: – математичне сподівання або, в термінах теорії надійності, середній час безвідмовної роботи об'єкту; - середнє квадратичне відхилення від середнього часу безвідмовної роботи.

Функція досягає максимуму при , тобто це таке значення тривалості роботи об’єкта, при якій частота відмов максимальна.

Графіки функцій і зображені на рис. 1.5.

Рис. 1.5

Чим більше значення , тим більш широкою стає крива розподілу, тому що характеризує розсіювання часу безвідмовної роботи. Найбільша кількість відмов відбувається поблизу точки ; так в межах від до виникає 68% відмов.

Ще одним розподілом, який широко застосовується в теорії надійності, є розподіл Вейбула. Це проста штучна модель, характер якої змінюється у широких межах в залежності від її параметрів. Спочатку ця модель була запропонована для оцінки міцності матеріалів, але в подальшому знайшла широке використання для оцінки надійності. Ймовірність безвідмовної роботи у цьому випадку

(1.9)

де та - параметри моделі. Орієнтовно значення = 0,2...0,4 –

для електронних пристроїв із спадаючою функцією інтенсивності відмов і = 1,2...1,4 – для механічних пристроїв з поступовим характером відмов.

Завершуючи цей розділ, зауважимо ще раз, що всі згадані розподіли є лише математичними моделями фізичних процесів, що відбуваються у внутрішній структурі компонентів і матеріалів, з яких вони побудовані. І тільки знання цих процесів може дати більш достовірну інформацію для прогнозування технічного стану об’єкта на тривалий період. До того ж потрібно розуміти, що, враховуючи статистичний характер поняття надійності, не можна сподіватися на велику точність розрахунків надійності (більшість фахівців з надійності вважає, що помилка на порядок в таких розрахунках не є чимось винятковим).

В особливо відповідальних випадках, коли, наприклад, електронна апаратура застосовується для управління реальними об’єктами, які можуть становити небезпеку для людей або довкілля (ядерні установки, космічна апаратура, транспортні засоби, тощо) необхідно проводити натурні випробування на надійність достатньо великої кількості виробів з тим, щоб одержати розподіл, який відповідає реальним умовам експлуатації.