21.Елементарна комбінаторика.Правила суми та правило добутку.

  В основі розв’язування багатьох комбінаторних задач лежать два основних правила – правило суми і правило добутку. У комбінаториці розглядається вибір і розміщення елементів деякої скінченної множини на основі якихось умов. 

Правило суми  Якщо елемент множини А можна вибрати m способами, а елемент множини В – n способами, то елемент множини А або В можна вибрати m+n способами.

Правило добутку  Якщо елемент множини А можна вибрати m способами, а після цього елемент множини В – n способами, то А і В можна вибрати (m • n) способами.

22.Сполуки без повторень.

Сполуками із різних елементів по називають множини складені із різних елементів взятих із , які розрізняються хоча б одним елементом (склад відіграє роль, а порядок ні): .

23. Сполуки з повтореннями: число різних сполук із різних елементів по обчислюється за формулою:

24. Бином Ньютона. Это формула, представляющая выражение ( a + b ) ⁿ  при положительном целом  n  в виде многочлена:

            

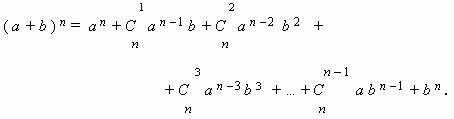
Заметим, что сумма показателей степеней для  a  и  b  постоянна и равна n.

П р и м е р  1 . 

Трикутник Паскаля.

Ряди трикутника Паскаля умовно пронумеровані згори, починаючи з нульового, й числа в нижньому ряді відносно чисел у попередньому ряді завжди розміщені ступінчасто й навскіс. Побудувати цей трикутник просто. Кожне число в кожному ряді одержуємо, додавши два числа, розміщені вгорі (зліва і справа). Якщо зліва або справа немає числа, підставляємо нуль на його місце. Наприклад, перше число в першому ряді 0 + 1 = 1, тоді як числа 1 і 3 в третьому ряді утворюють число 4 в четвертому ряді: 1 + 3 = 4.

Правило Паскаля стверджує: якщо

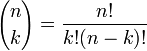
k-й біноміальний коефіцієнт в біноміальному ряді для (x + y)ⁿ, тоді

для будь-якого додатного цілого n і будь-якого цілого k між 0 і n

Ряди трикутника Паскаля умовно пронумеровані згори, починаючи з нульового, й числа в нижньому ряді відносно чисел у попередньому ряді завжди розміщені ступінчасто й навскіс. Побудувати цей трикутник просто. Кожне число в кожному ряді одержуємо, додавши два числа, розміщені вгорі (зліва і справа). Якщо зліва або справа немає числа, підставляємо нуль на його місце. Наприклад, перше число в першому ряді 0 + 1 = 1, тоді як числа 1 і 3 в третьому ряді утворюють число 4 в четвертому ряді: 1 + 3 = 4.

Правило Паскаля стверджує: якщо

k-й біноміальний коефіцієнт в біноміальному ряді для (x + y)ⁿ, тоді

для будь-якого додатного цілого n і будь-якого цілого k між 0 і n

25. JV-множиною   Q   називається множина, що містить N-елементів.

Нехай Аh А2,   А„ - підмножини JV-множини Q . Позначи-

мо через   А   доповнення множини А{.   А. = Q \ А   і N(A) -

кількість елементів множини А. Має місце формула:

                        П

N(A\A2 ...An) = N-^ N{A\) +   ^ N{AiAj) -

і=\        \<i<j<n

-    ^N(AJA]Ak) + ... + (-V)"N(AlA2...An) (1.2.1).

\<i<j<k<n

n

Наслідок. Візьмемо у формулі Q = [j4  і врахуємо, що

z=l

N = iV(fi) = N([J 4 ) та 4 ' Л • • A ={JA=0- Отримаємо формулу:

N({JAI) = ^TN(AI)- '^jN(AiAj)+   ^ІУ(44-Л)~

z=l       z=l       \<i<j<n \<i<j<k<n

-... + (-l)n'lN(Al-A\-...■ An) (1.2.2).

Це   формули   включень   та   виключень,   або   формули решета.