
 Міністерство
освіти і науки України
Міністерство
освіти і науки України
Національний технічний університет України „КПІ”
Факультет інформатики та обчислювальної техніки
Кафедра технічної кібернетики
Розрахунково-графічна робота
з дисципліни «Системи обробки сигналів та зображень»
Перевірив: К.т.н., доцент Ігнатенко В.М.
|
Виконала: студентка II курсу гр. ІК- 02 Максимова Є.
|
 Київ
2012
Київ
2012
Зміст
Індивідуальне завдання 3
Короткі теоретичні відомості 4
Розрахункова частина роботи 6
Табличні та графічні результати розрахункової частини роботи 7
Індивідуальне завдання
Варіант № 1
Завдання № 1
Дискретизовний
сигнал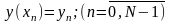 заданий своїми значеннями у наступній
таблиці:
заданий своїми значеннями у наступній
таблиці:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
0,2 |
0.4 |
0.6 |
0.8 |
1 |
1.2 |
1.4 |
1.6 |
1.8 |
|
-0.8 |
-0.6 |
0.2 |
0.7 |
0.9 |
1.4 |
0.8 |
0.4 |
0.1 |
-0.2 |
Провести згладжування (апроксимацію) даних за допомогою полінома
 Вирахувати
значення різниць (відхилень) між
вихідними і згладженими даними, знайти
максимальне по модулю значення їх
різниці та суму квадратів відхилень
між вихідними та згладженими даними.
Подати усі вихідні дані та результати
обчислювань у відповідній табличній
та графічній формі.
Вирахувати
значення різниць (відхилень) між
вихідними і згладженими даними, знайти
максимальне по модулю значення їх
різниці та суму квадратів відхилень
між вихідними та згладженими даними.
Подати усі вихідні дані та результати
обчислювань у відповідній табличній
та графічній формі.
Завдання № 2
Розрахувати
на основі ДПФ спектр (амплітудний
 та фазовий
та фазовий
 )
наступного дискретизованого сигналу
,
заданого своїми дискретами у наступній
таблиці:
)
наступного дискретизованого сигналу
,
заданого своїми дискретами у наступній
таблиці:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
|
0 |
1.38 |
0.32 |
-0.32 |
-1.38 |
0 |
1.38 |
0.32 |
-0.32 |
-1.38 |
Визначити період дискретизації спектра, інтервал його визначення та число дискрет. Результати розрахунків подати у відповідній табличній та графічній формі.
Короткі теоретичні відомості
Завдання 1
Апроксимація
– метод цифрового згладжування даних
коли шукану функцію
 необхідно збудувати між парами величин
необхідно збудувати між парами величин
 ,
,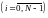 відповідно до певної стратегії
згладжування, наприклад, мінімізація
деякої міри близькості, не намагаючись
при цьому виконати умову точного збігу
експериментальних даних зі значеннями
функції наближення.
відповідно до певної стратегії
згладжування, наприклад, мінімізація
деякої міри близькості, не намагаючись
при цьому виконати умову точного збігу
експериментальних даних зі значеннями
функції наближення.
Розв’язок задачі апроксимації виконується в залежності від обраної міри близькості , чисельне значення якої визначає ступінь близькості значень заданого сигналу і його апроксимуючої функції.
Одним із видів апроксимації є апроксимація за допомогою поліномів, що полягає в наступному:
формуються значення вихідного сигналу;
 де
N – кількість дискрет
де
N – кількість дискрет
обирається поліном відповідного ступеня;
Наприклад, поліном другого ступеня:

обирається міра близькості між заданим сигналом і значенням степеневого поліному;
Функція, що оцінює ступінь міри близькості сигналу та поліному n-го ступеня:

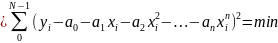
значення шуканих коефіцієнтів знаходяться за умови рівності похідної від квадратичної міри близькості нулю по кожному коефіцієнту поліному:
 (1)
(1)
(1) - це система з n+1 лінійних алгебраїчних
рівнянь,
де
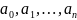 -
шукані коефіцієнти. Якщо існує розв’язок
цієї системи, то вона дає найкраще
наближення до заданої функції, у вигляді
функції степеневого поліному заданого
ступеня.
-
шукані коефіцієнти. Якщо існує розв’язок
цієї системи, то вона дає найкраще
наближення до заданої функції, у вигляді
функції степеневого поліному заданого
ступеня.
Завдання № 2
За
допомогою ДПФ (дискретного перетворення
Фур’є ) визначається спектр дискретизованого,
обмеженого по тривалості сигналу, що
заданий своїми дискретними значеннями.
Спектр дискретизованого сигналу є
періодичною функцією аргументу ω, тобто
кругової частоти ω з періодом
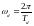 (в
якості аргументу також може виступати
циклічна частота
(в
якості аргументу також може виступати
циклічна частота
 ).
).
Відповідна формула для дискретного перетворення Фур’є:
 ,
де
,
де
 -
період
дискретизації;
-
період
дискретизації;
y( )
– дискретизований
сигнал;
)
– дискретизований
сигнал;
ω – кругова частота.
Алгоритм розрахунку ДПФ для обмеженого в часі дискретизованого сигналу:
1.
Розраховується частота
дискретизації
(кругова
 або циклічна
або циклічна
 ),
яка визначає величину періоду (частотного
інтервалу) на якому буде заданий шуканий
спектр:
),
яка визначає величину періоду (частотного
інтервалу) на якому буде заданий шуканий
спектр:

де
- інтервал дискретизації вихідної
функції
 ;
;
2.
Вираховуються комплексні
значення спектру
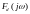 для кожної лінії спектру при таких
значеннях частоти
для кожної лінії спектру при таких
значеннях частоти
 ,
,
тобто з наступним кроком між сусідніми лініями спектру:

Кожна спектральна лінія складається з однієї дійсної та однієї уявної частини, тобто

3.
Для узгодження значень і розмірності
величин ДПФ з відповідним неперервним
спектром сигналу необхідно помножити
на період дискретизації
,
тобто
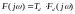 .
.
4. Розрахунки амплітудного та фазового спектрів виконуються згідно з наступними формулами:


 ,
де
,
де
- період дискретизації;
ωk – кругова частота.



