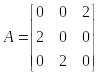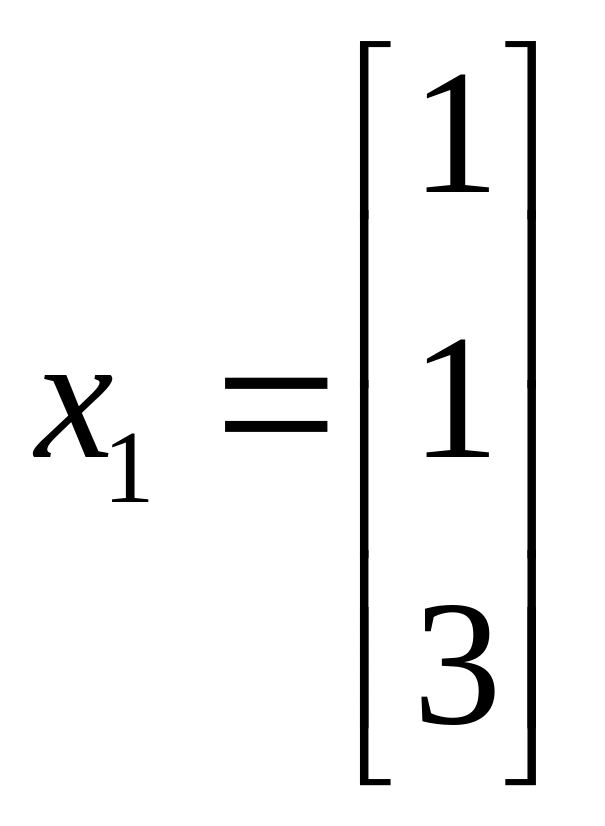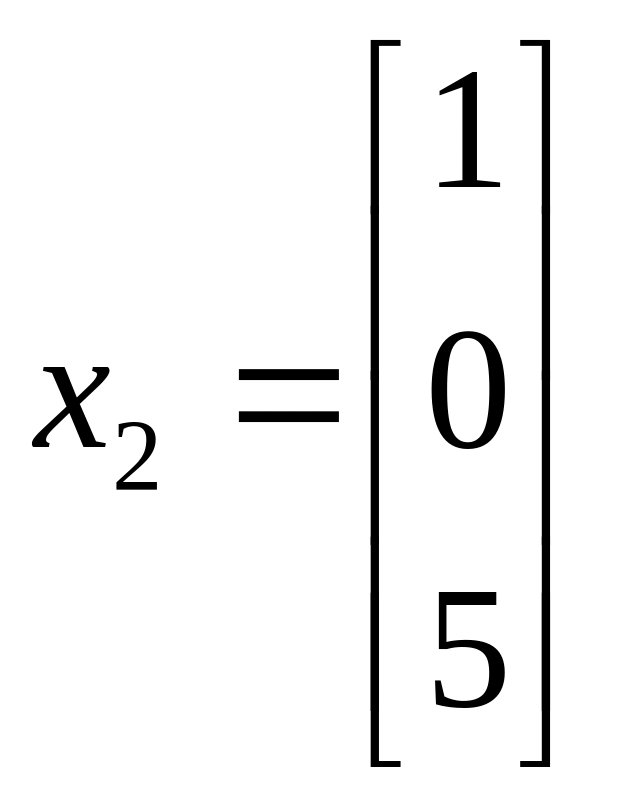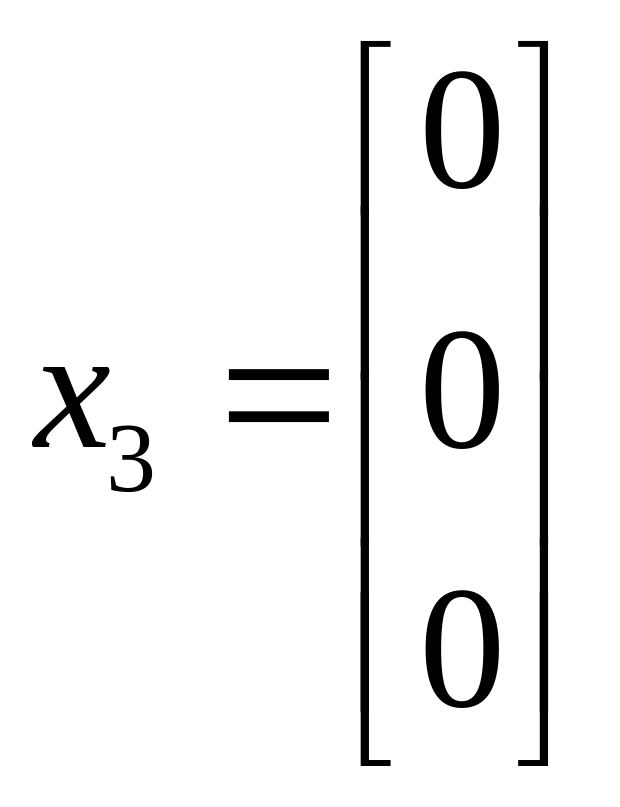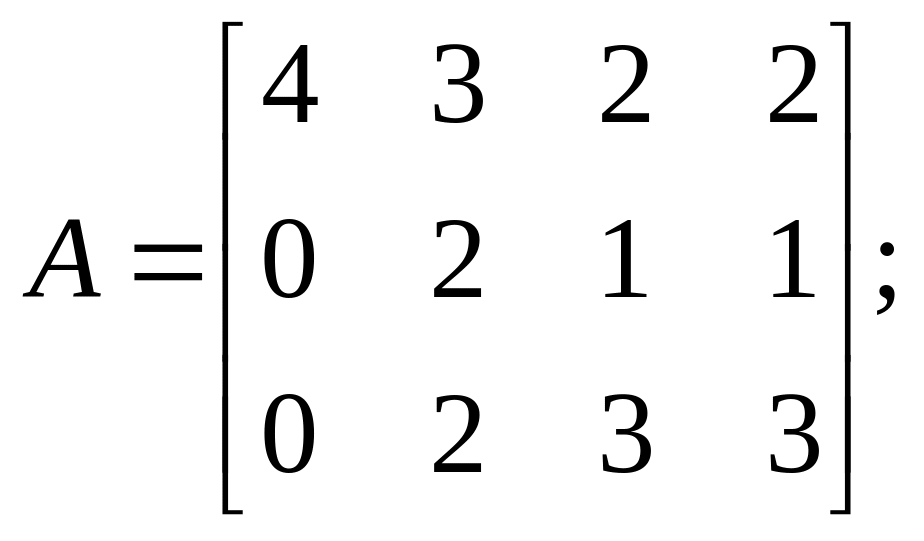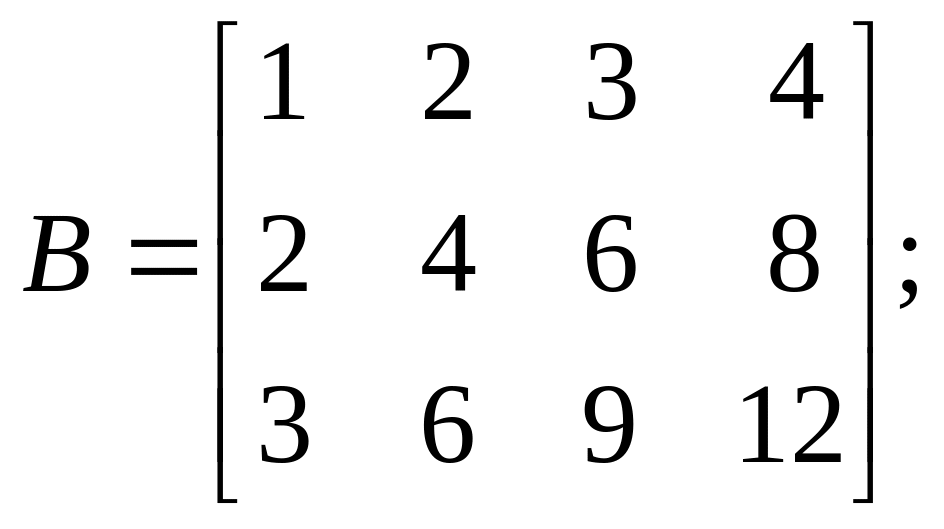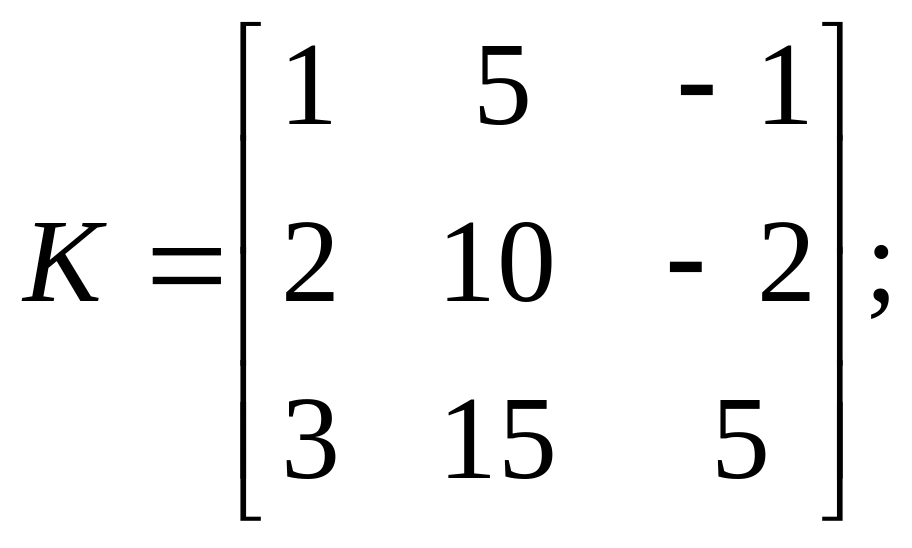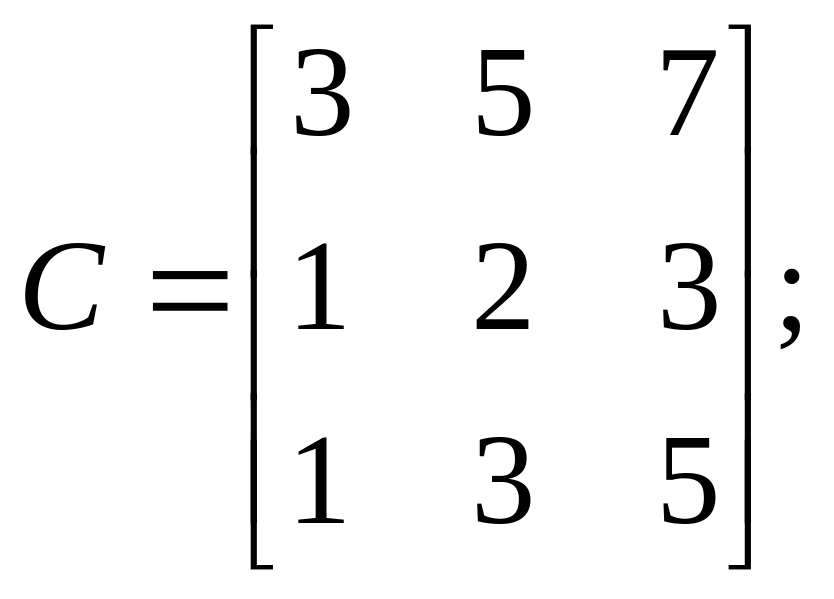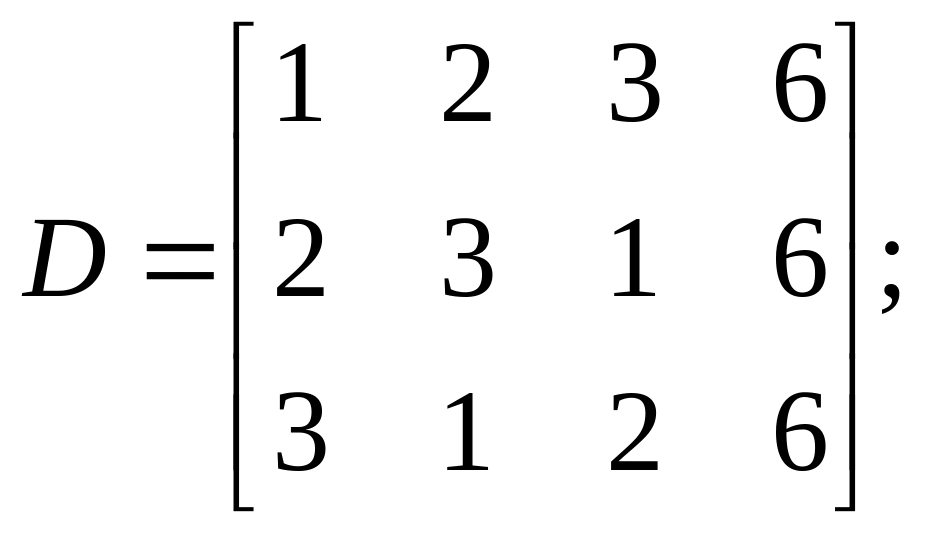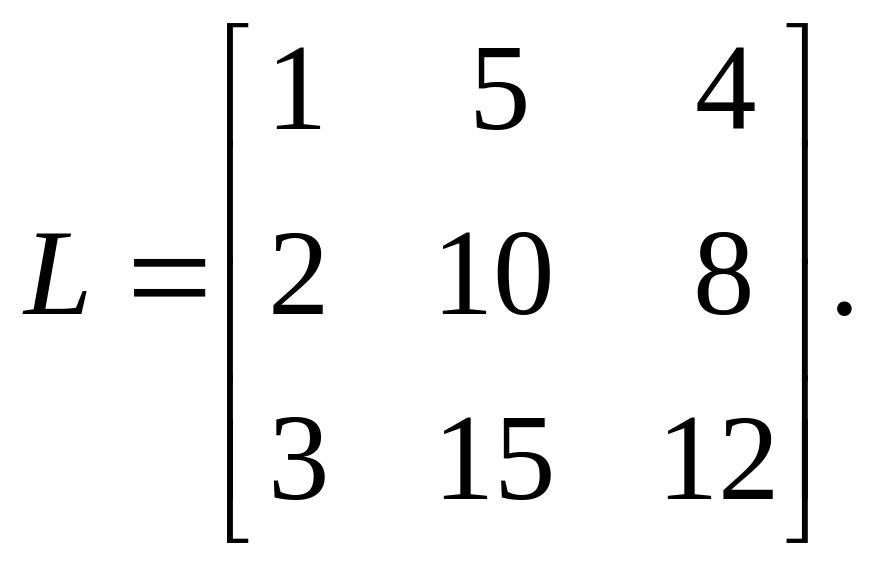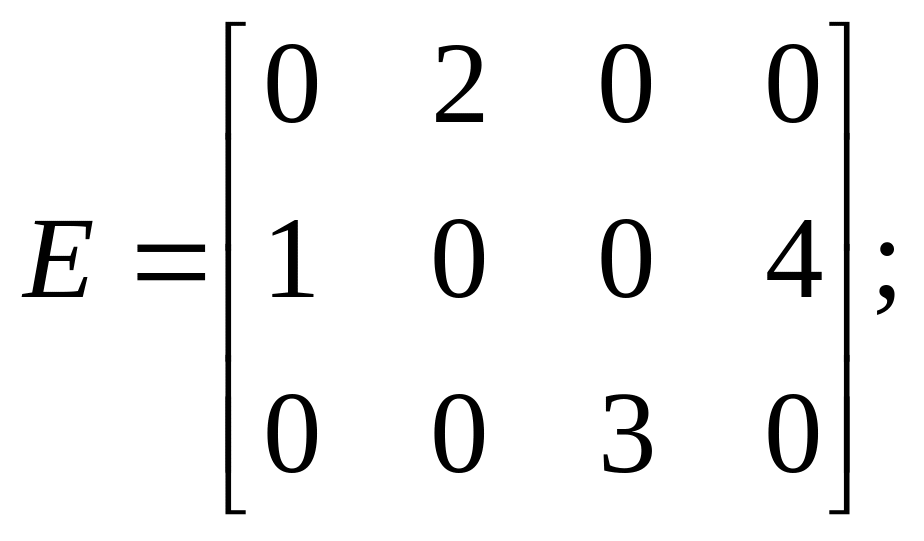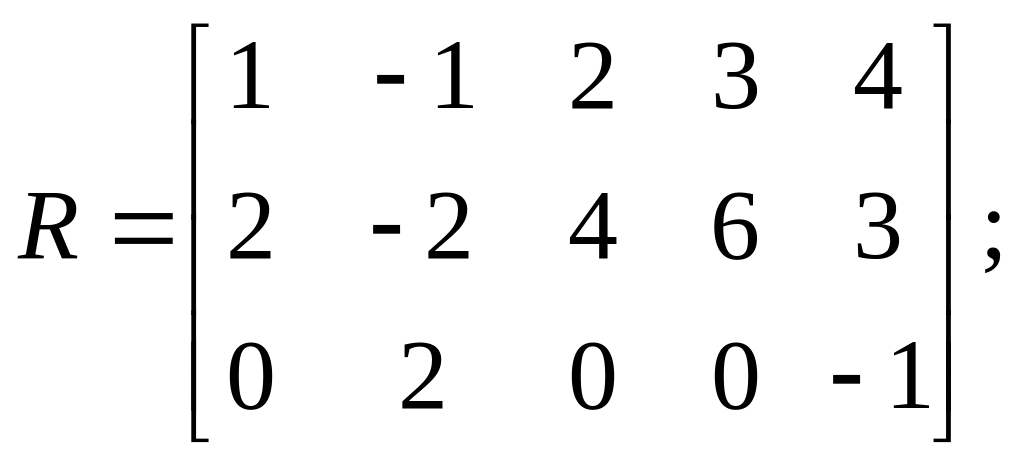Задачи по теме «Линейная алгебра»
Найти матрицу
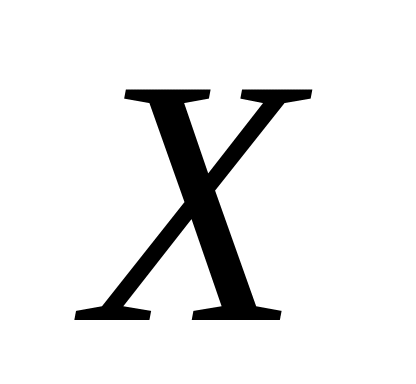 ,
если
,
если1). 2
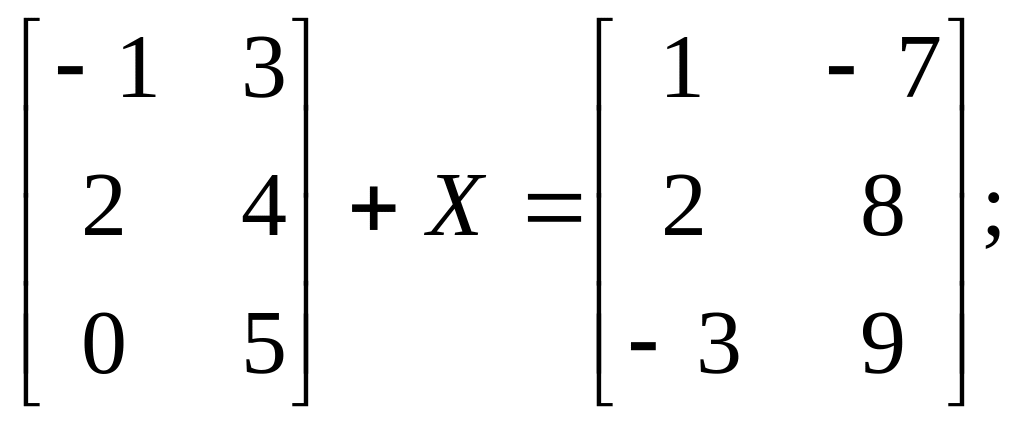
2).
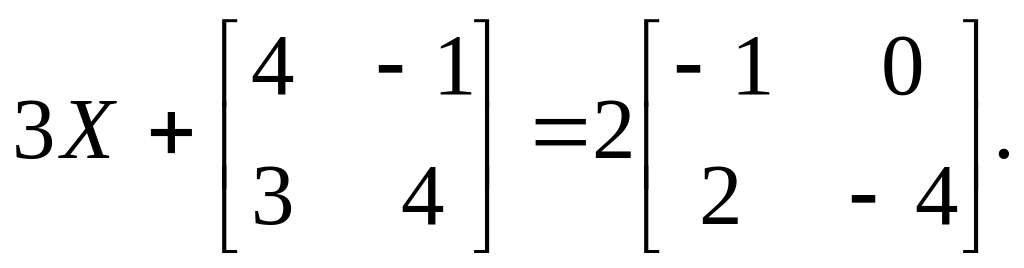
3).
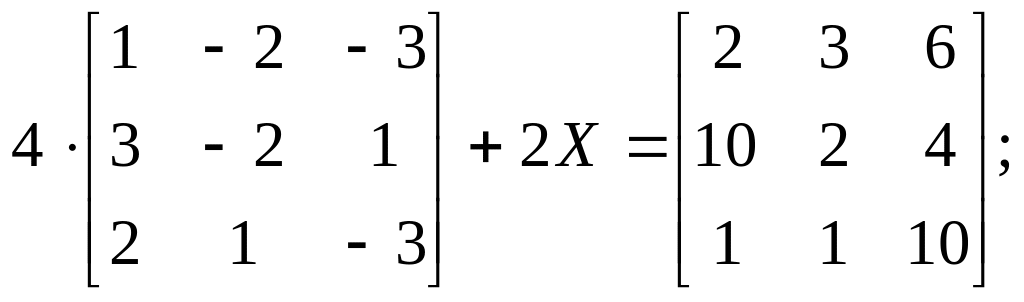
4).
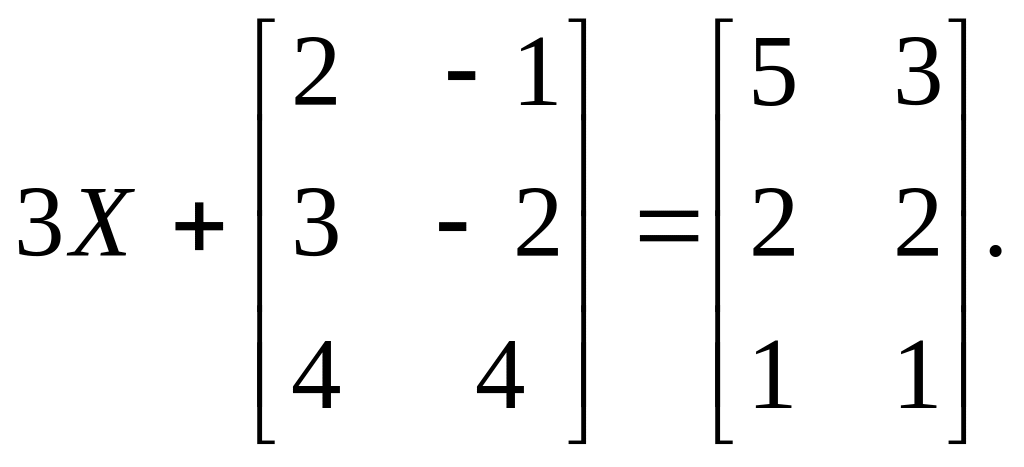
Найти
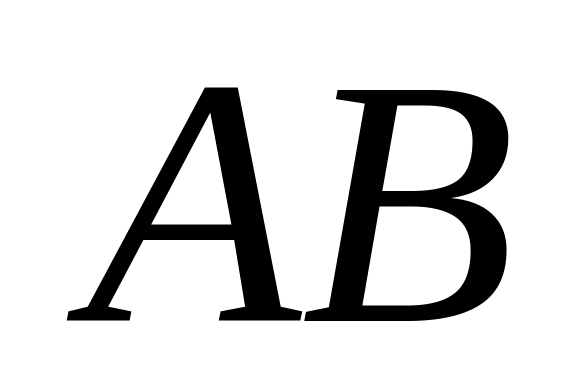 и
и
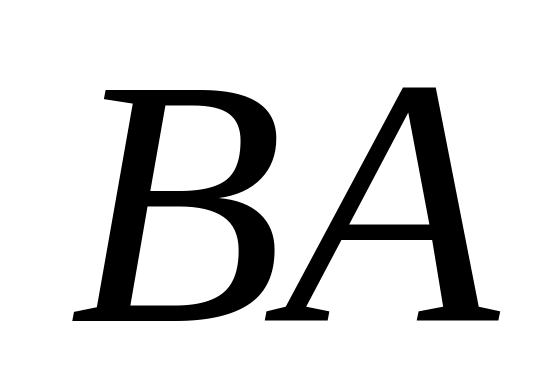 ,
если эти произведения существуют:
,
если эти произведения существуют:
-
1).
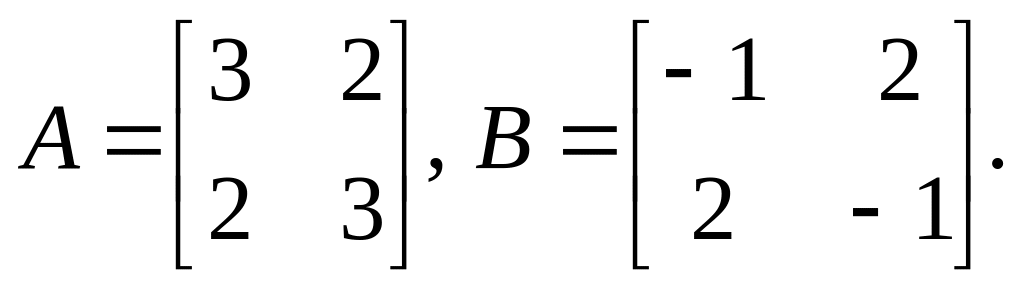
4).
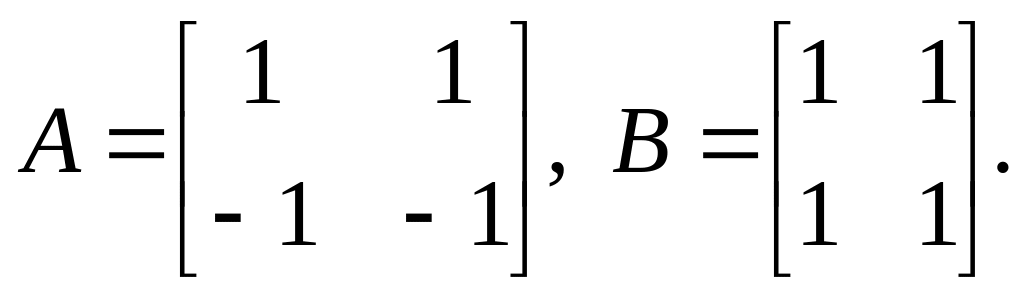
2).
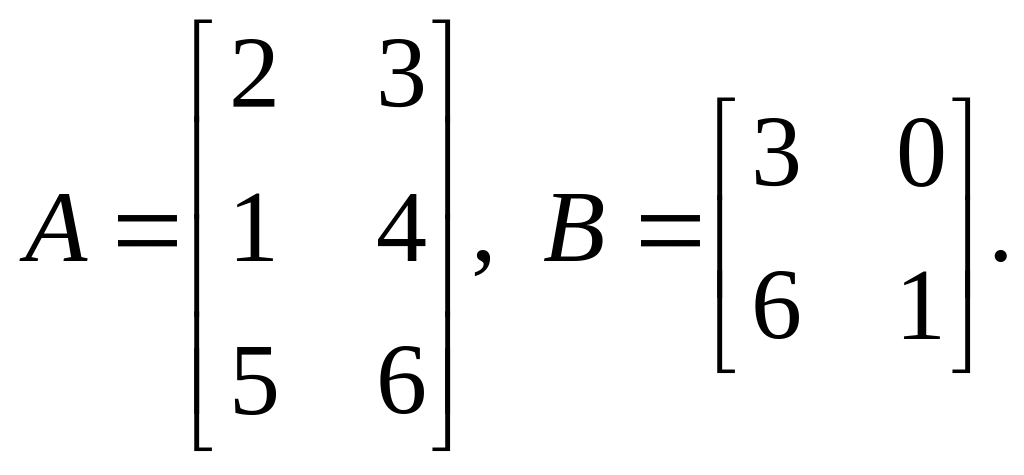
5).
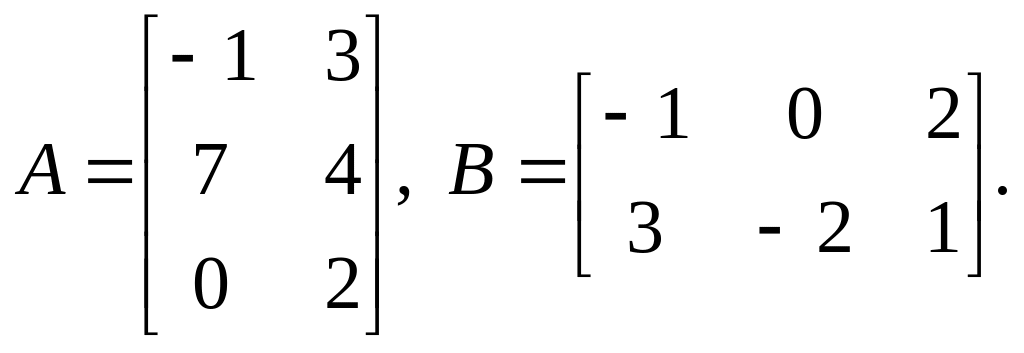
3).
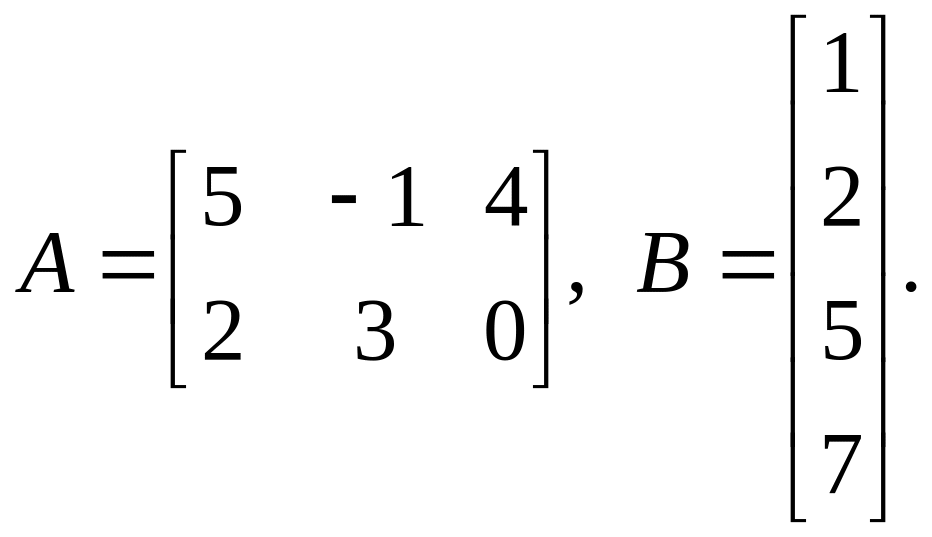
6).
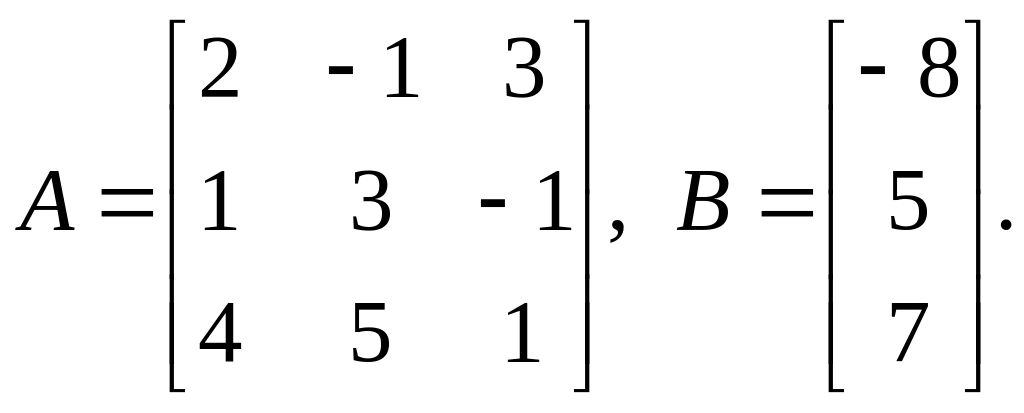
3.
Найти
![]()
а)
![]() б)
б)
![]()
4.
Найти
![]() и
и
![]()
а)
![]()
б)
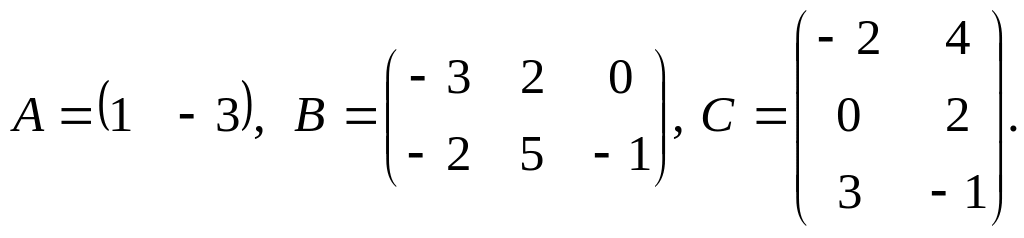
5.
Найти
![]()
а)
![]() б)
б)
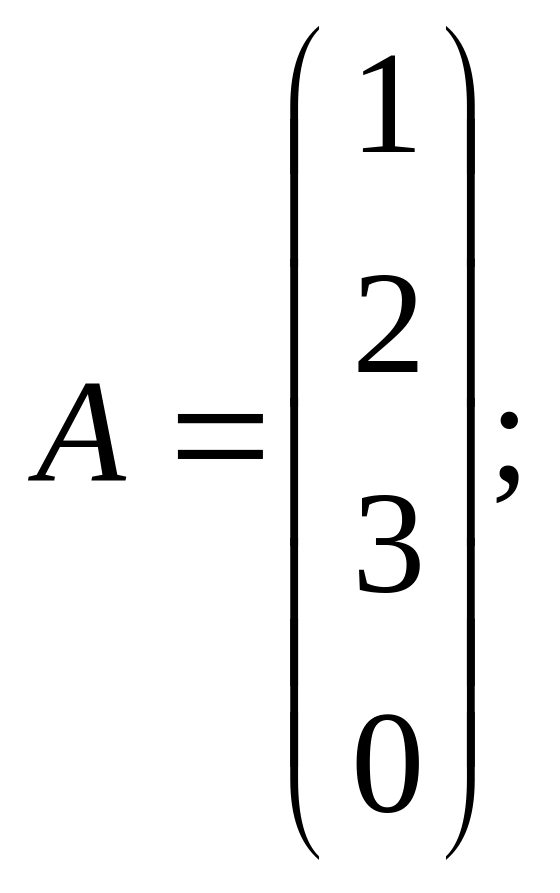 в)
в)
![]()
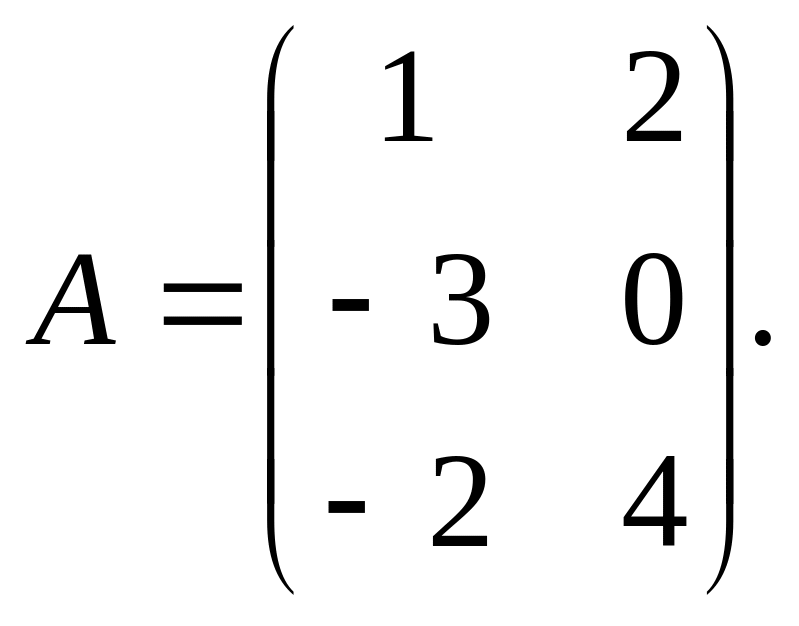
6.
Найти значение матричного многочлена
![]() если
если
а)
![]() ;
;
б)
![]()
в)
![]()
г)
![]()
д)
![]()
e)
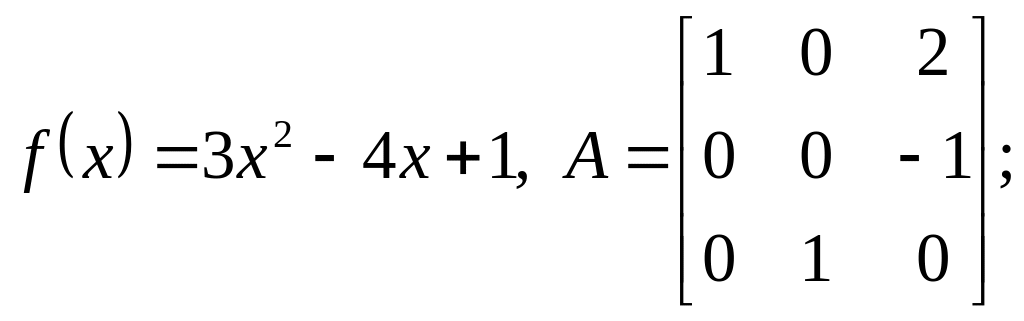
7. Вычислить определители:
-
1).
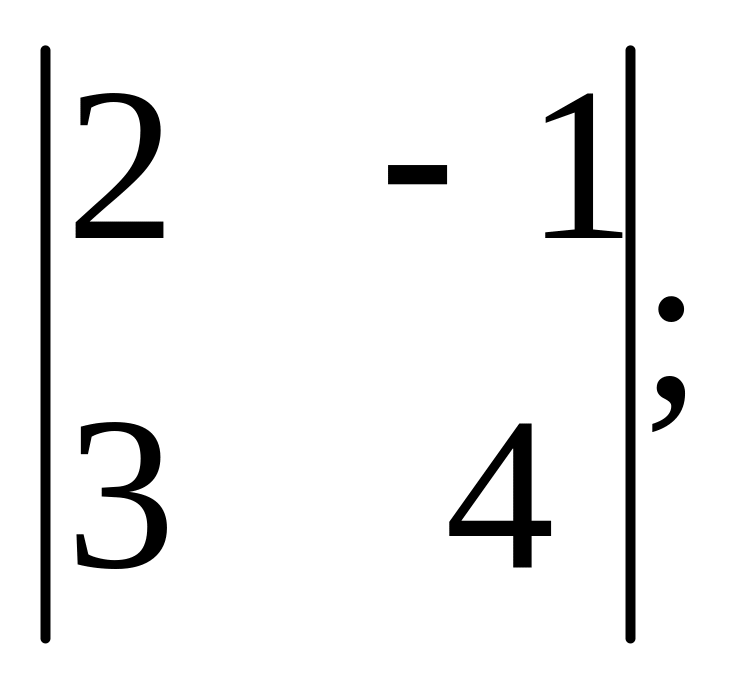
2).
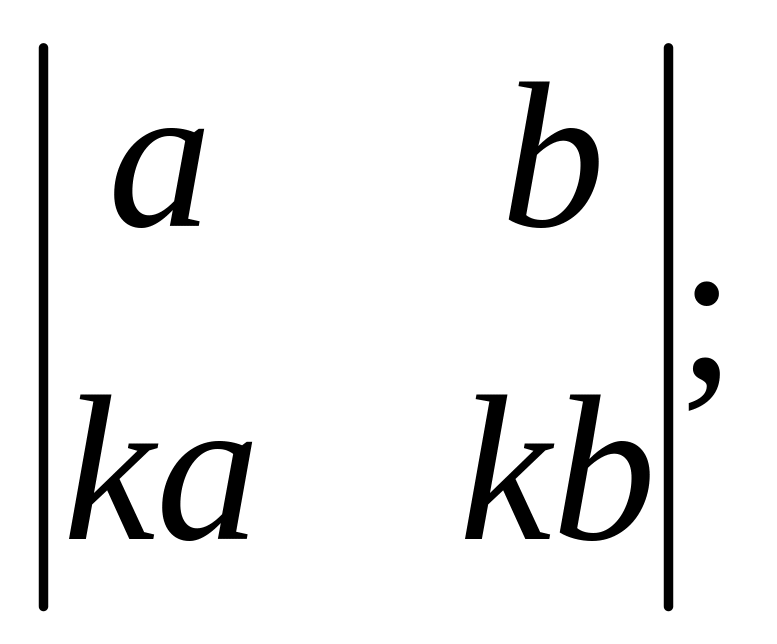
3).
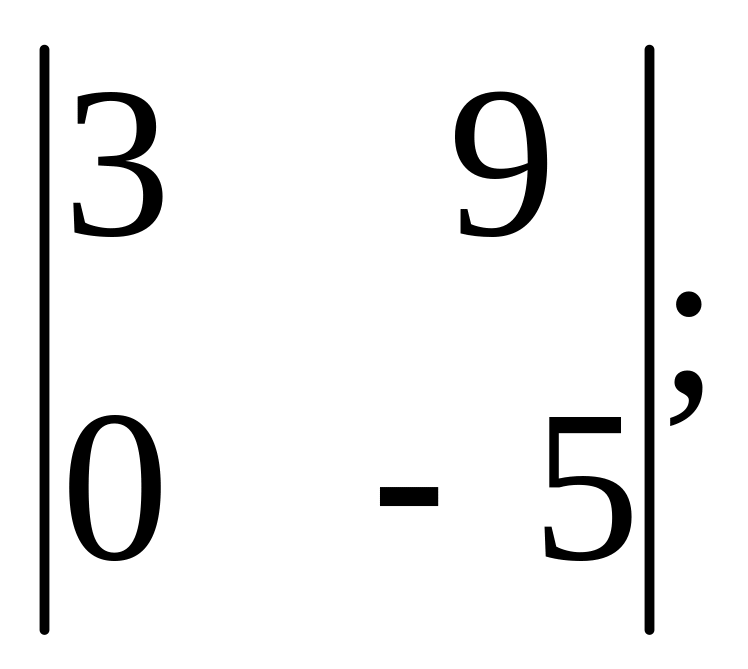
4).
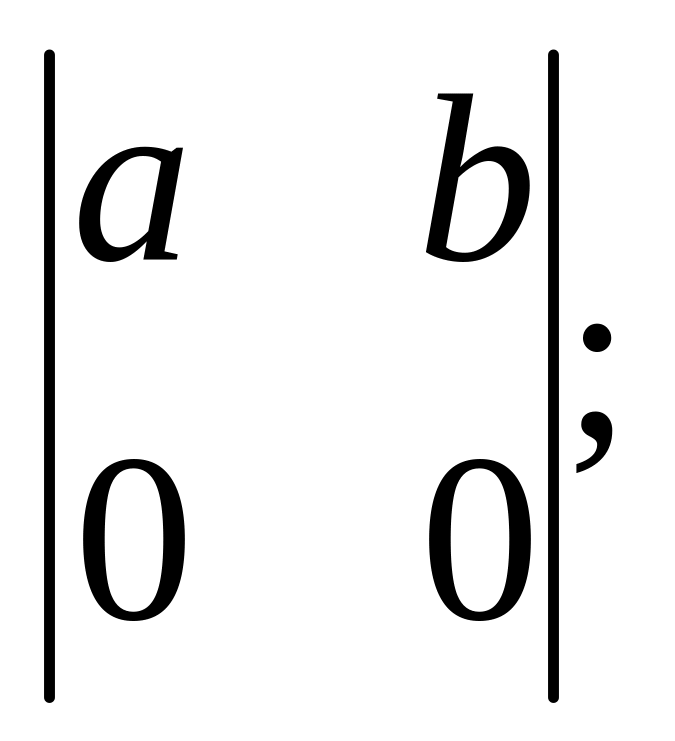
5).
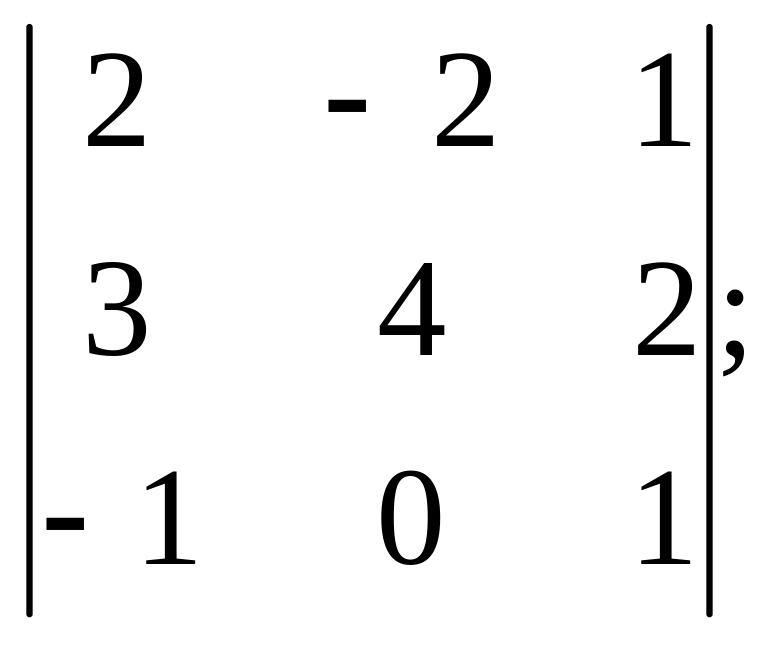
6).
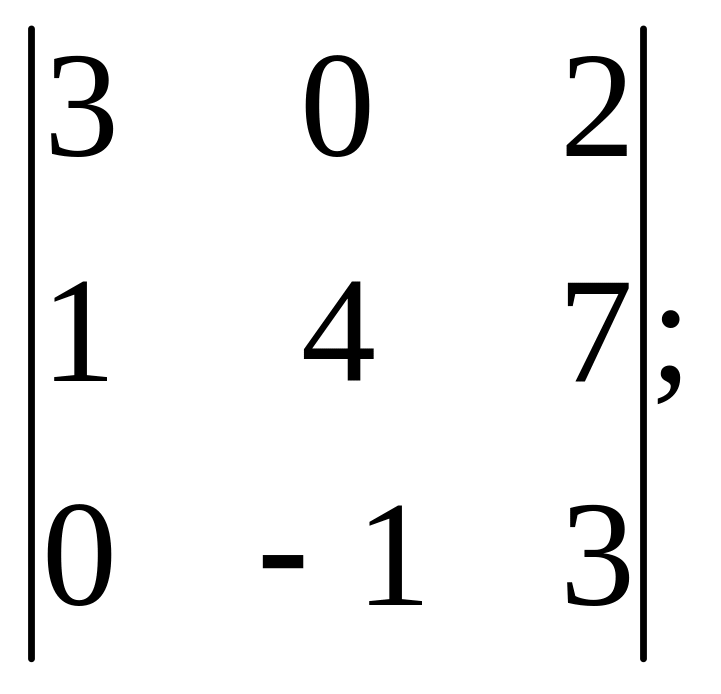
7).
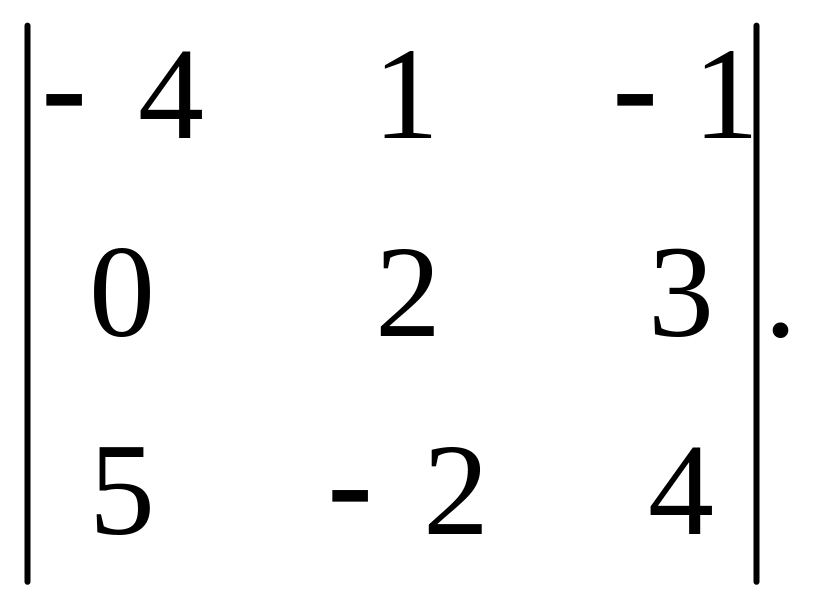
8).
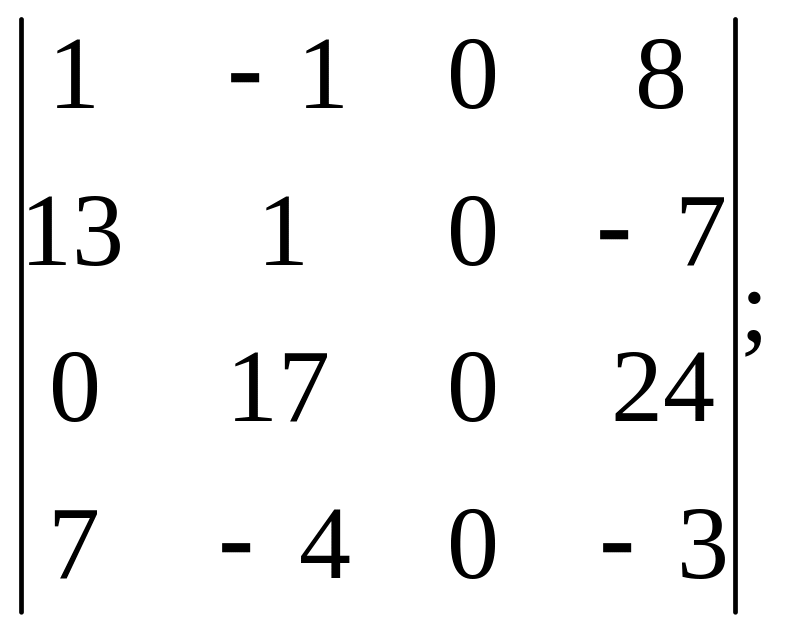
9).
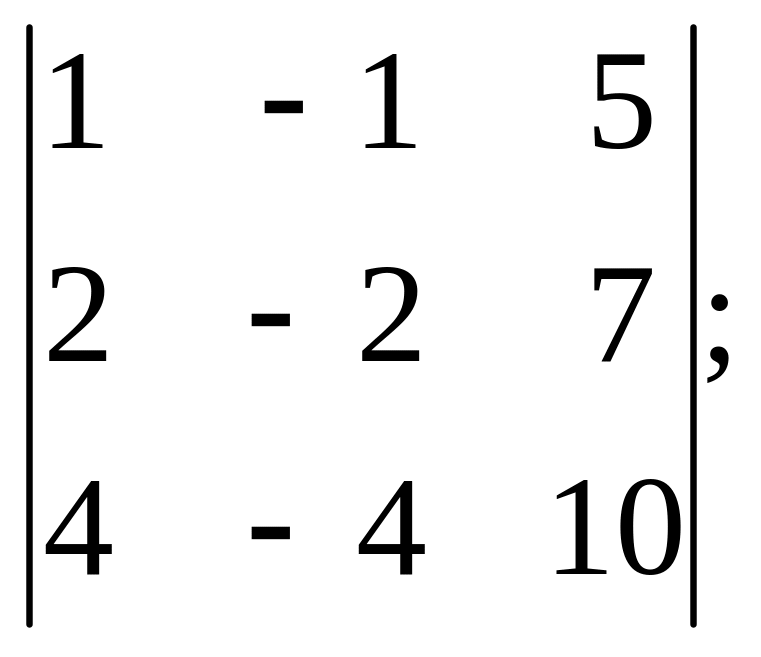
10).

11).

12).
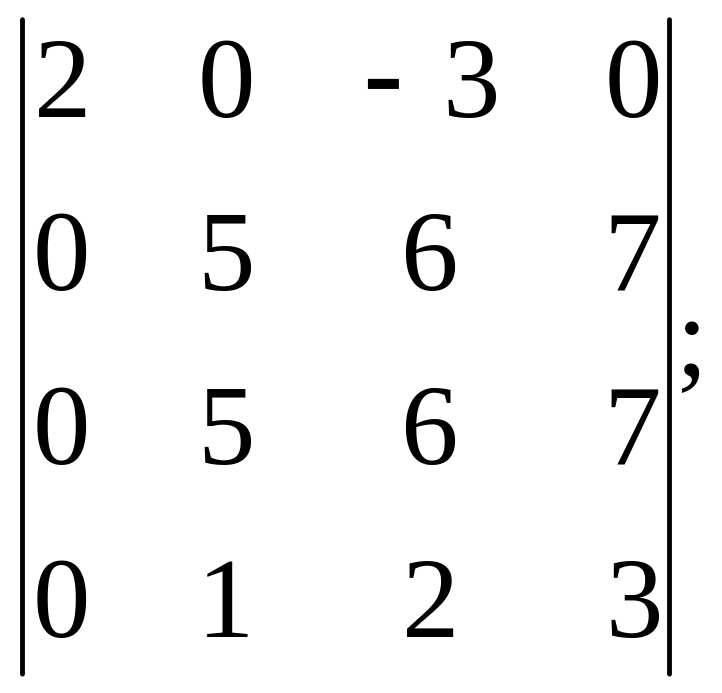
13).

-
14).
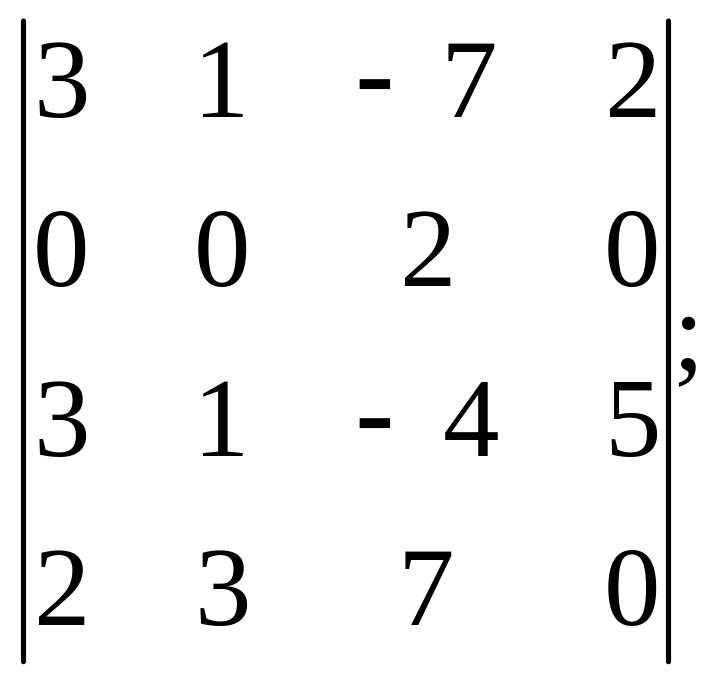
15).
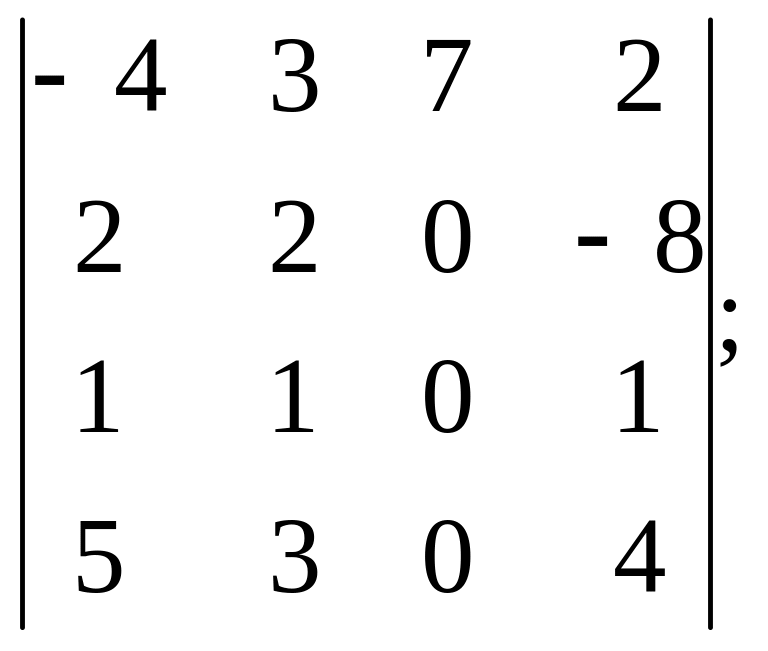
16).
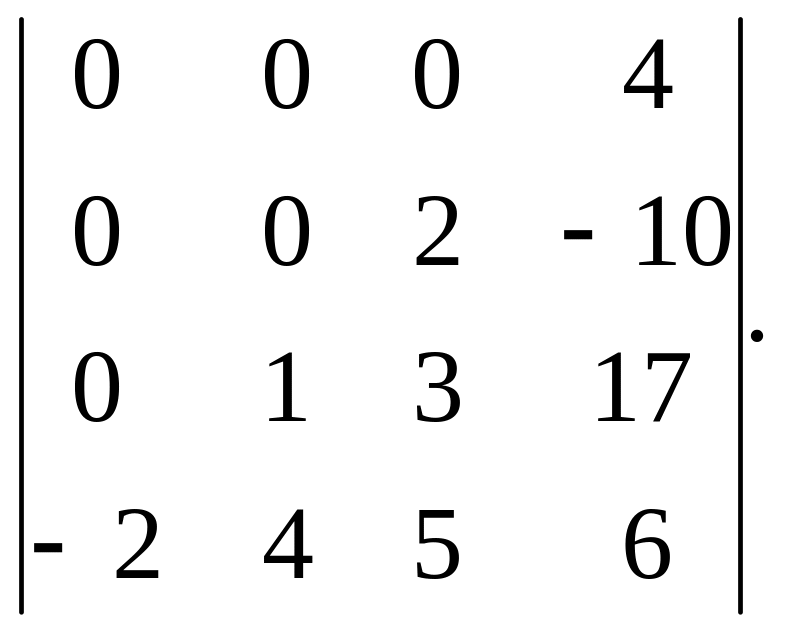
17).

18).
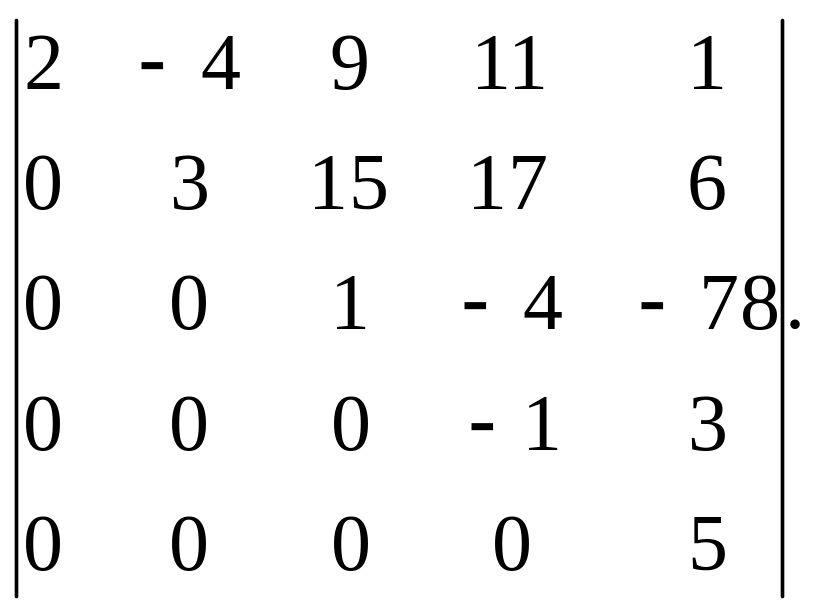
8.
Найти
![]() и сделать проверку, если
существует:
и сделать проверку, если
существует:
-
1).
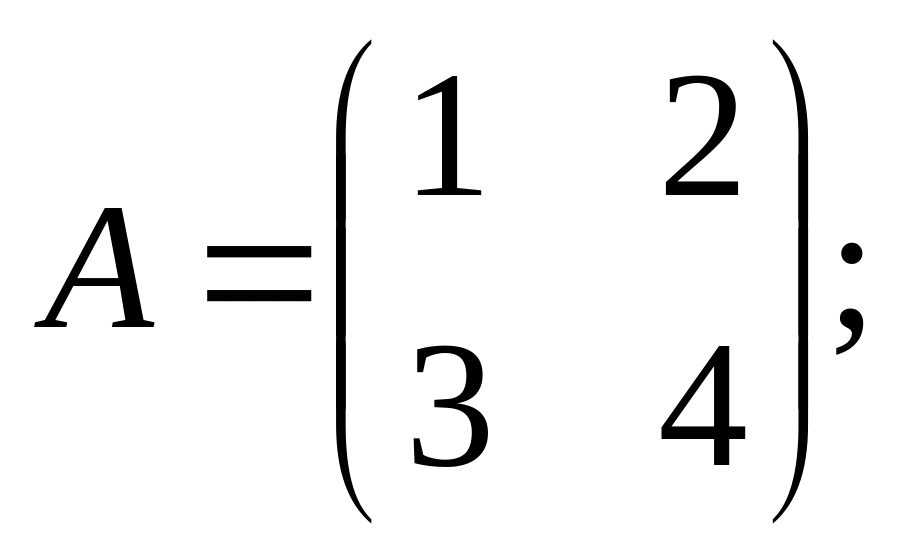
2).
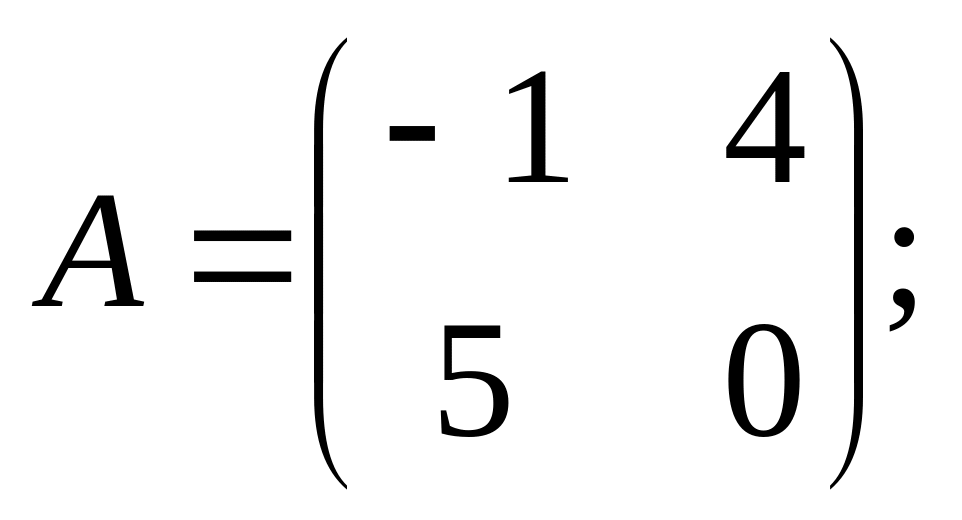
3).
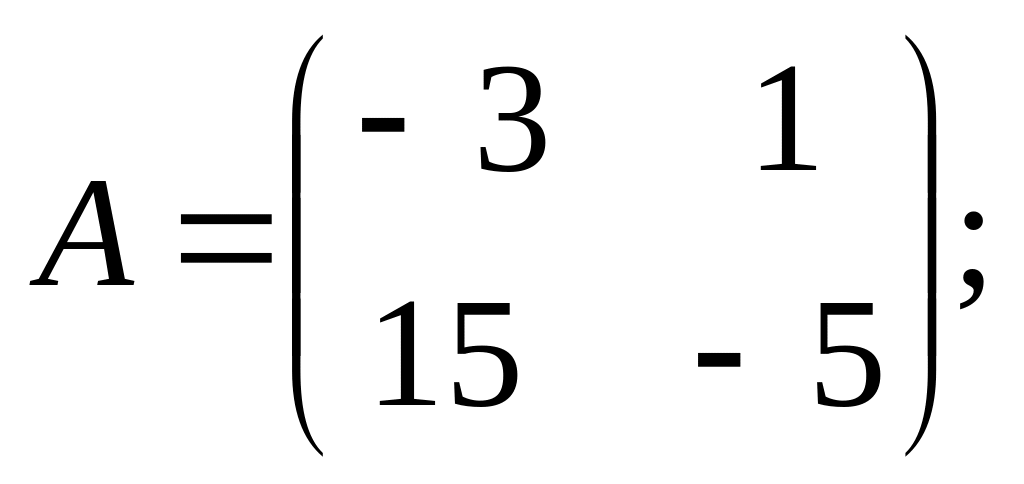
4).
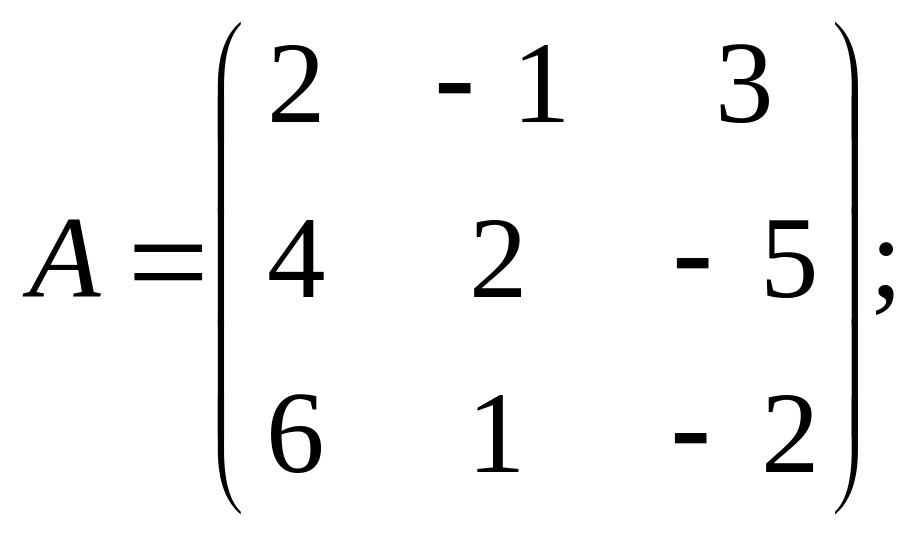
5).
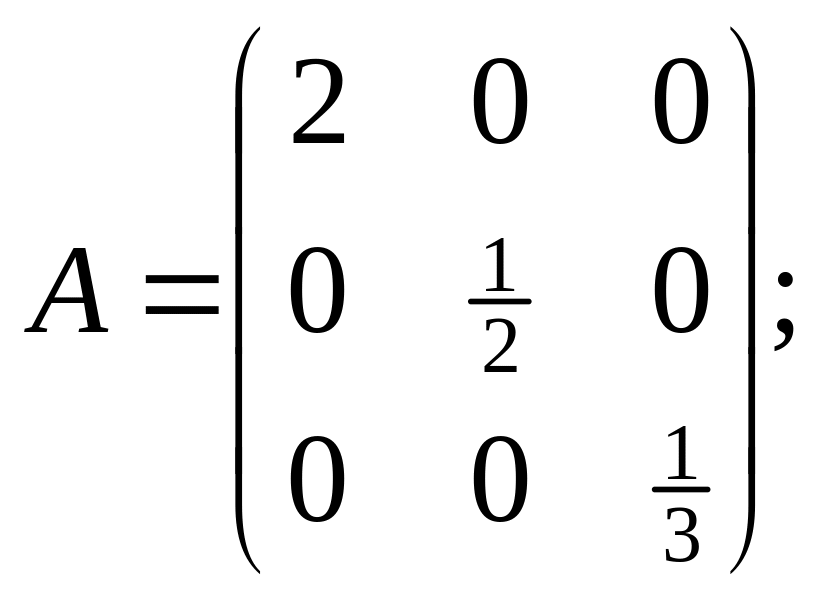
6).
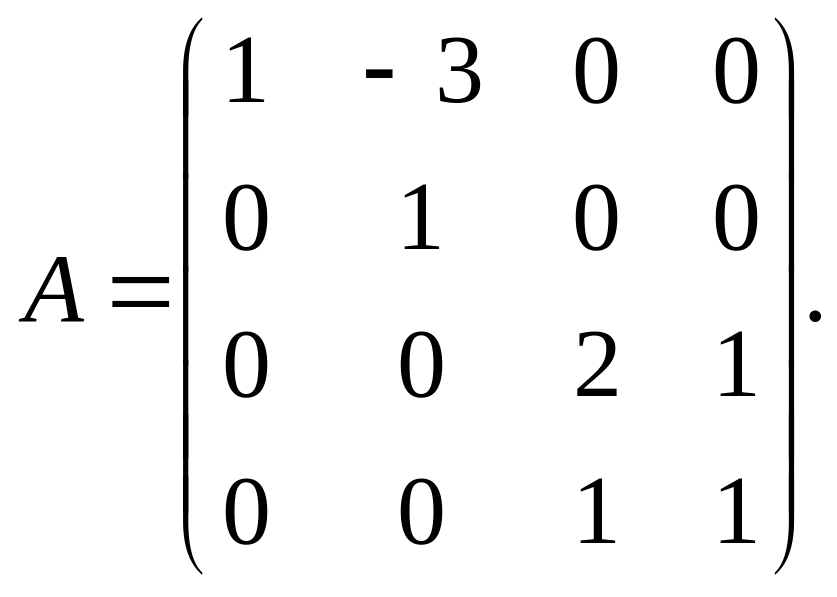
7).
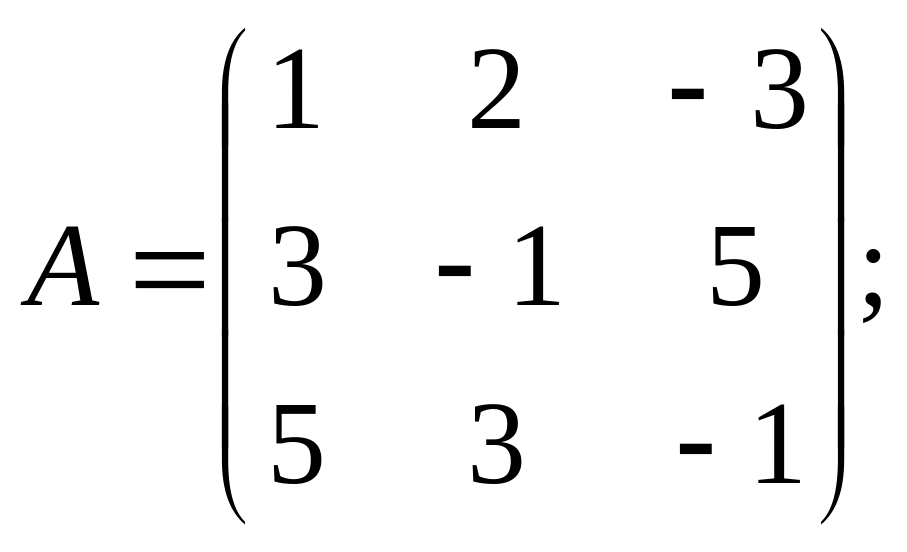
8).
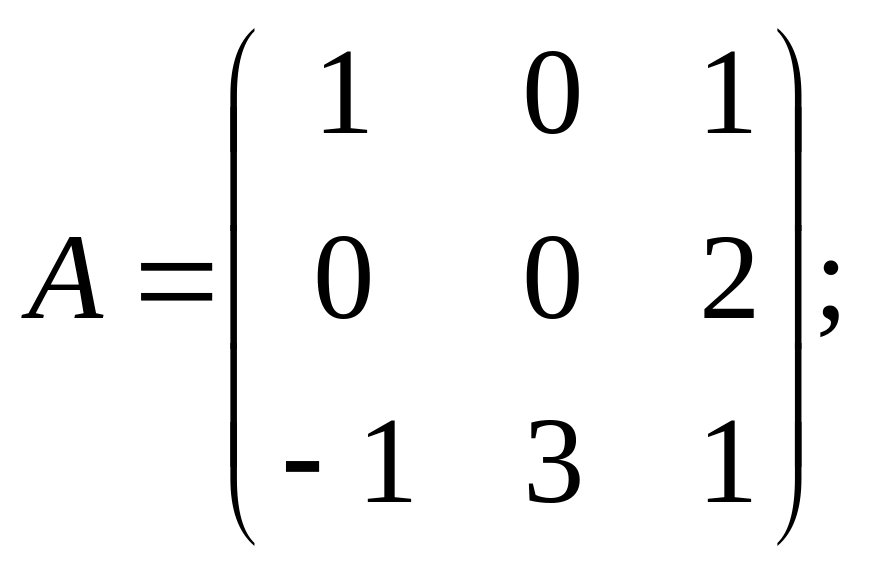
9).
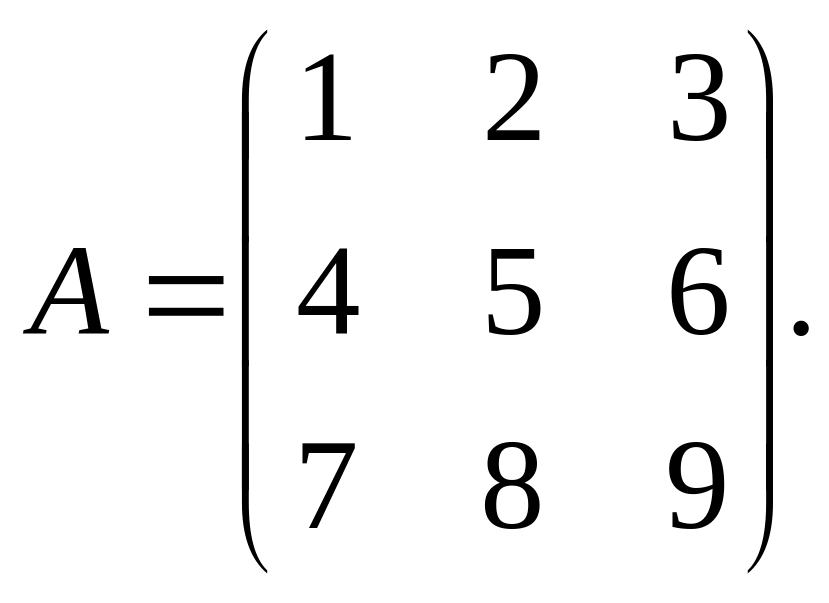
Решить системы линейных алгебраических уравнений а) методом Крамера; б) методом обратной матрицы; в) методом Гаусса:
1).
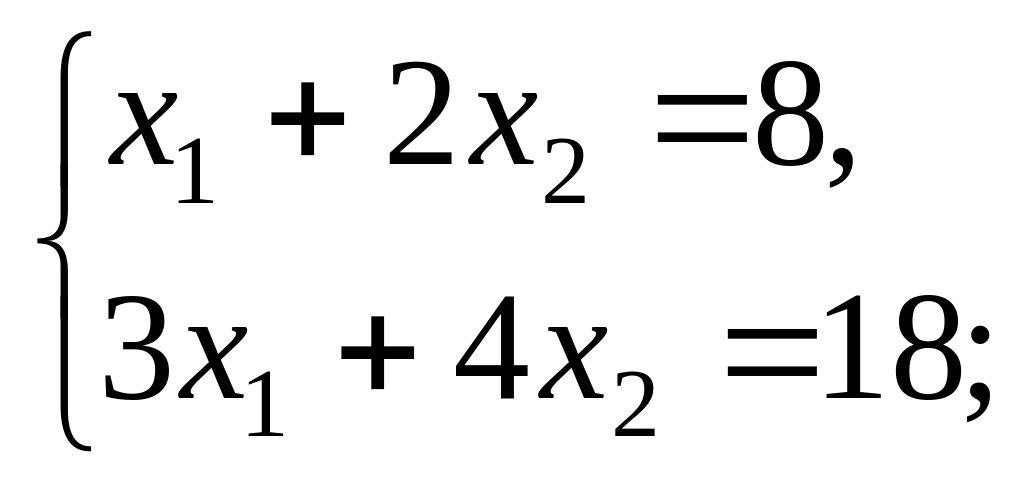
2).
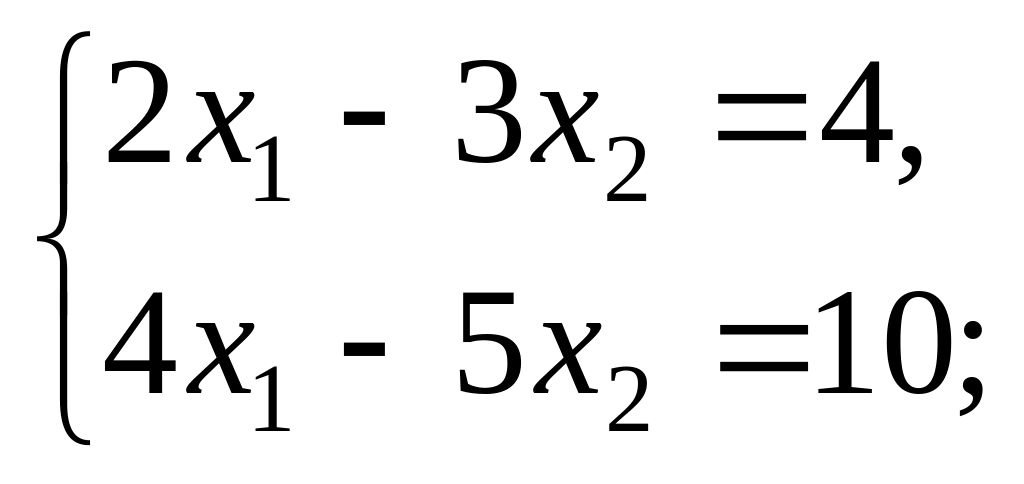
3).
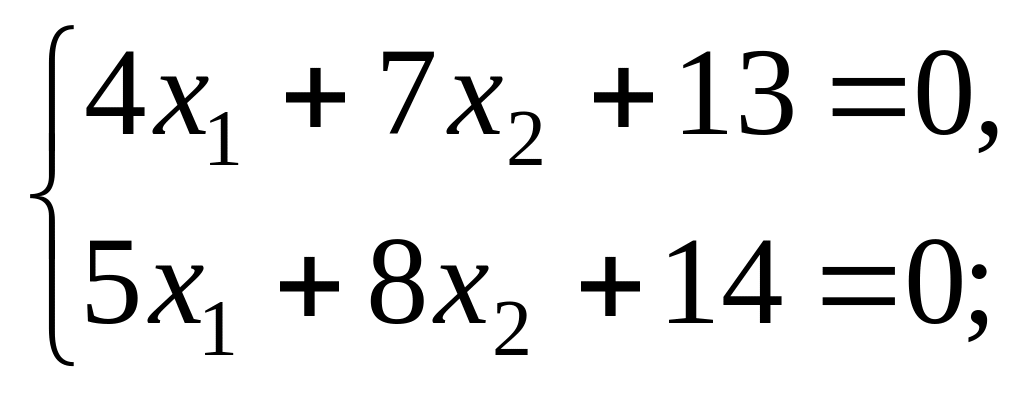
4).
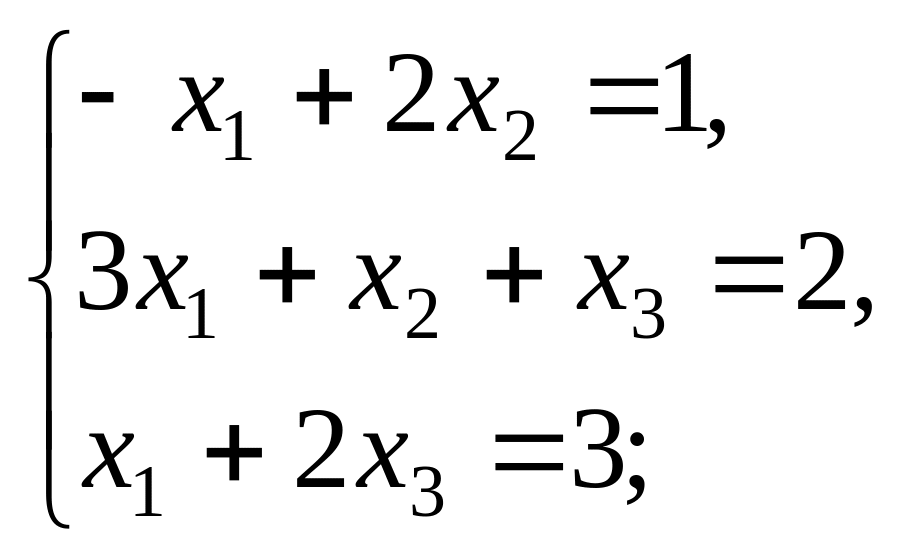
5).
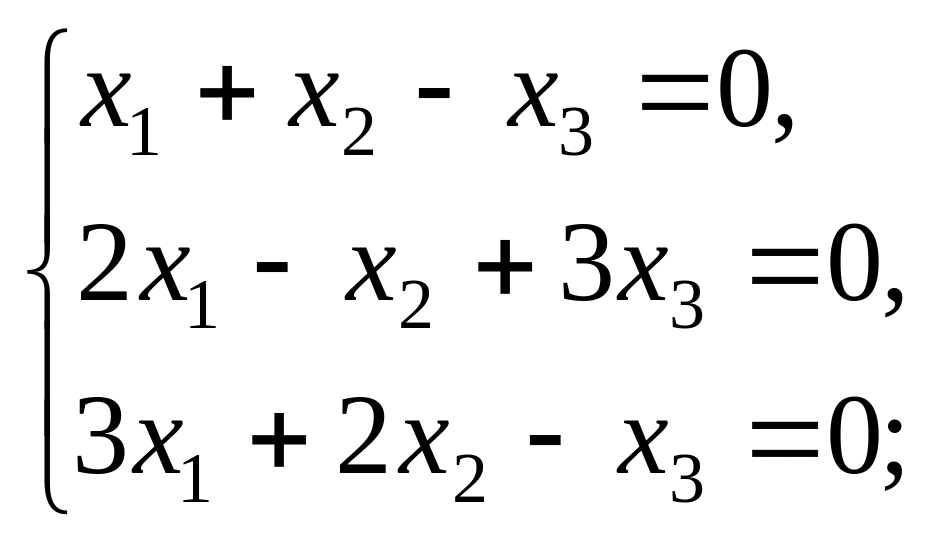
6).
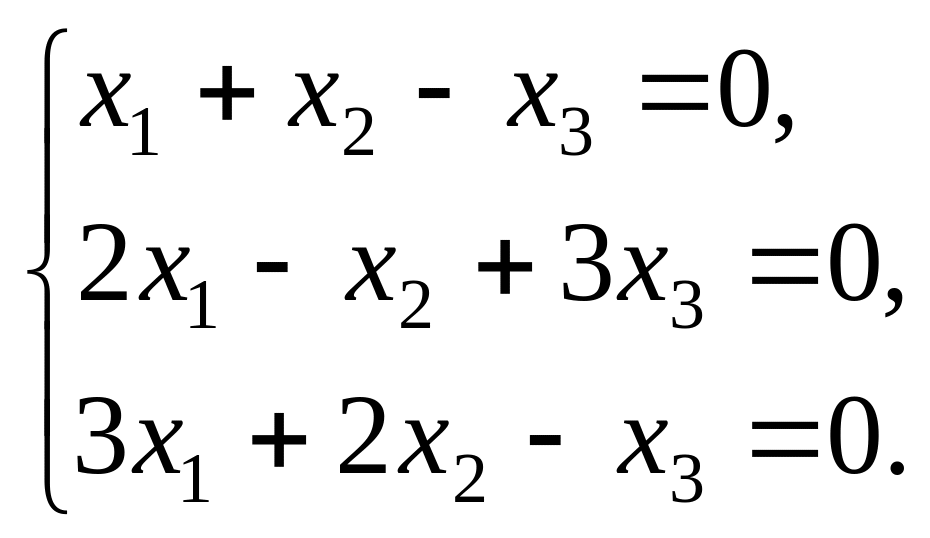
7).
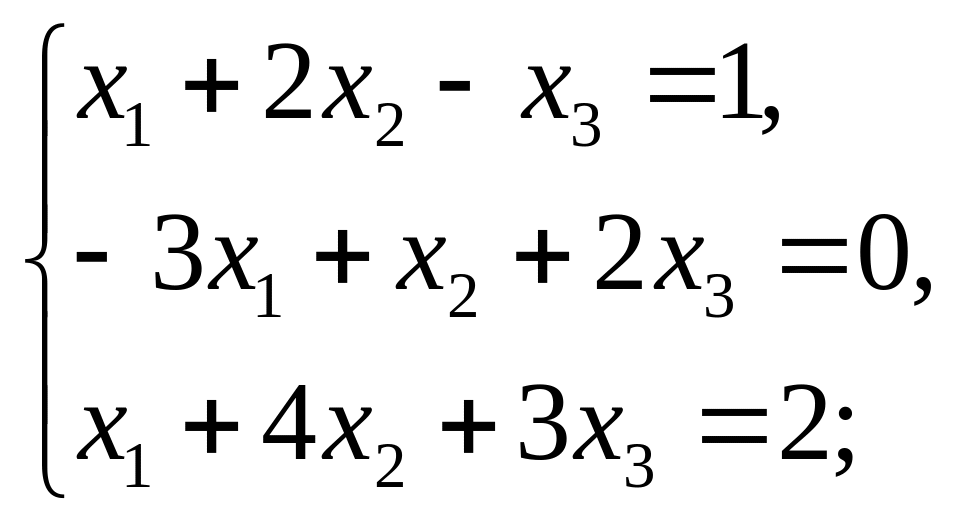
8).
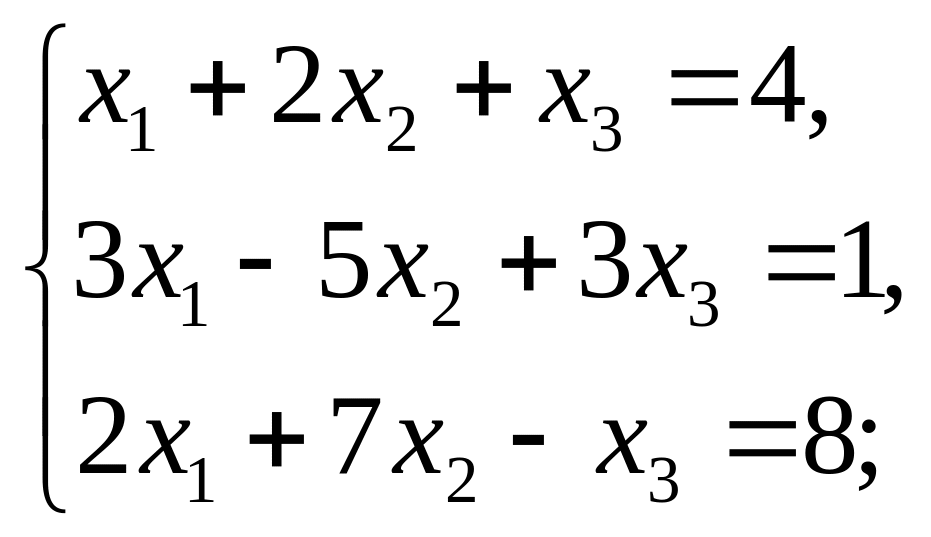
9).
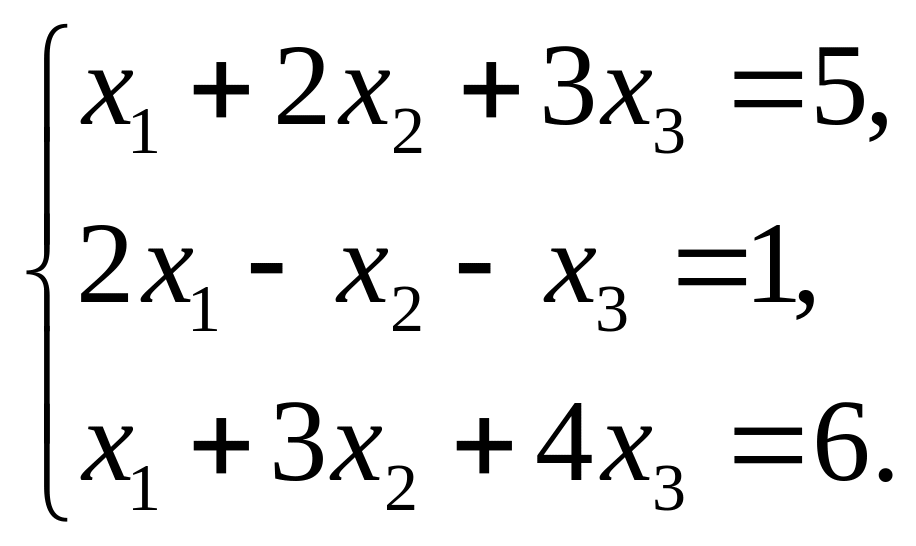
Найти решение системы
а)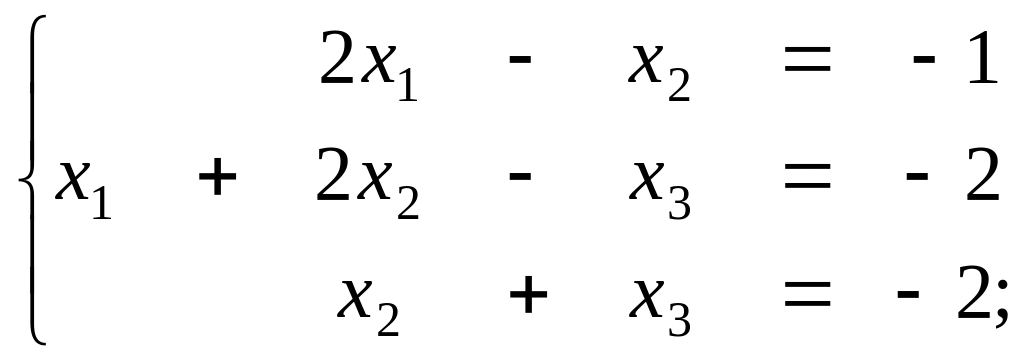 б)
б)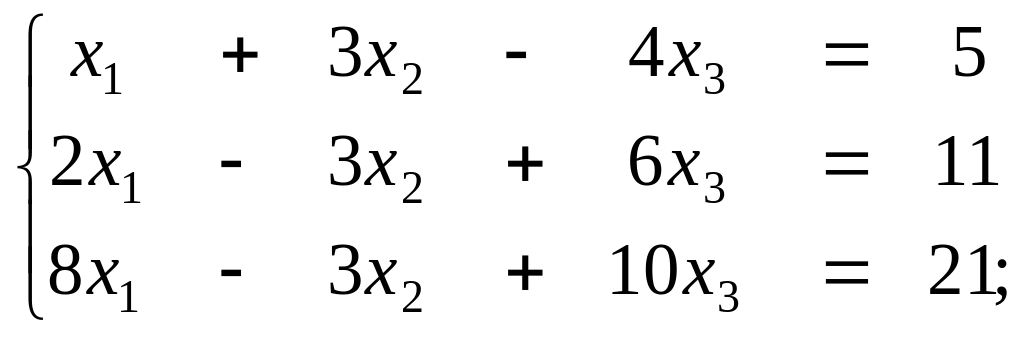
в)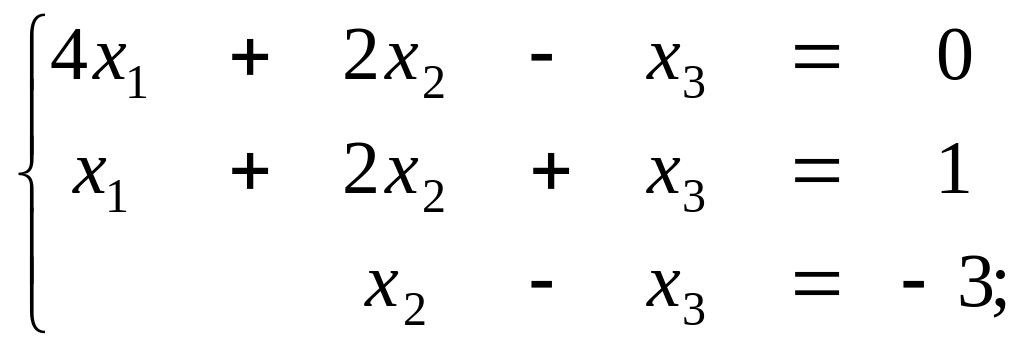 г)
г)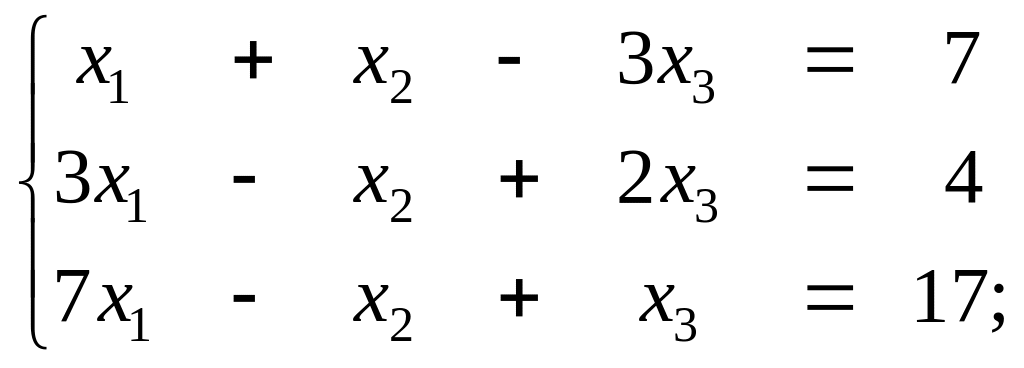
д)
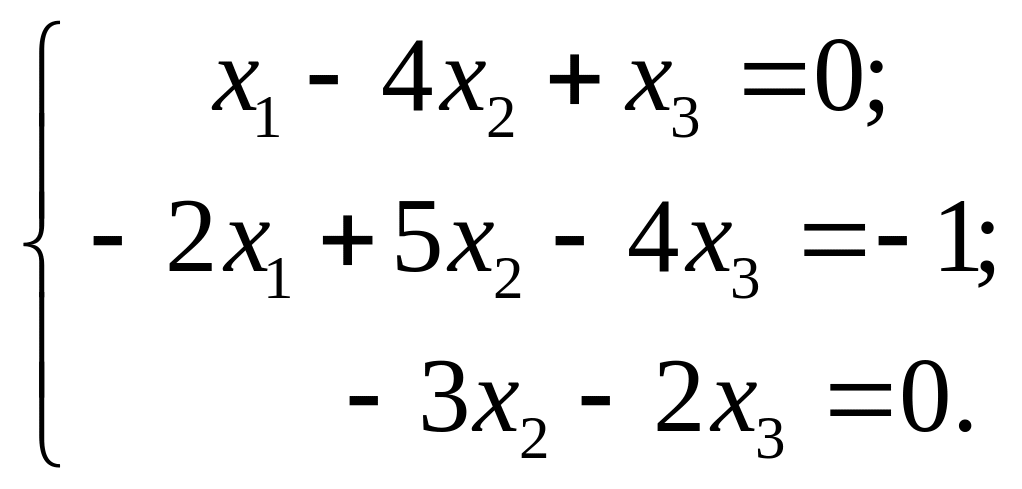 е)
е)
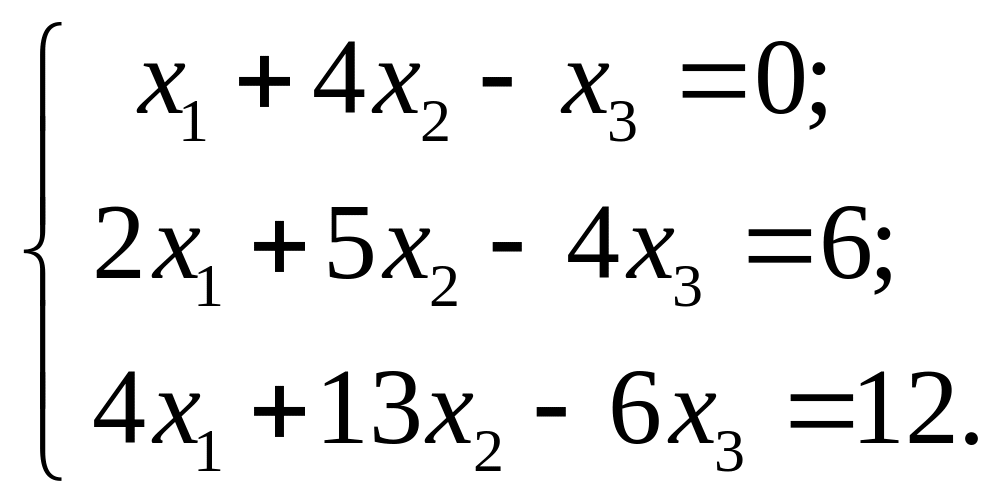
ж)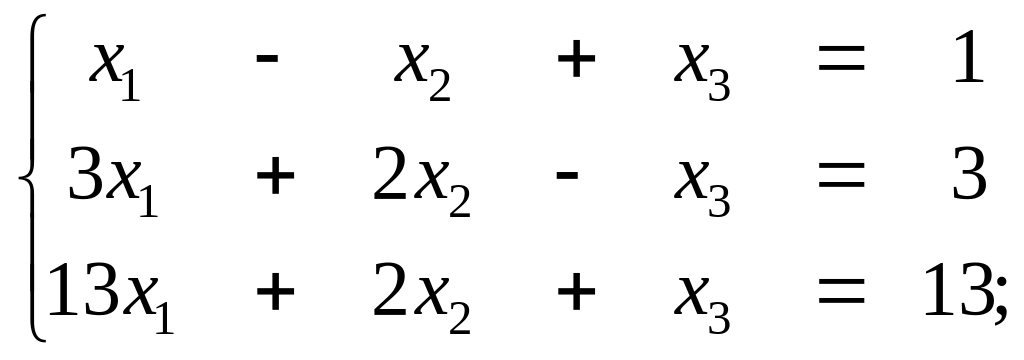 з)
з)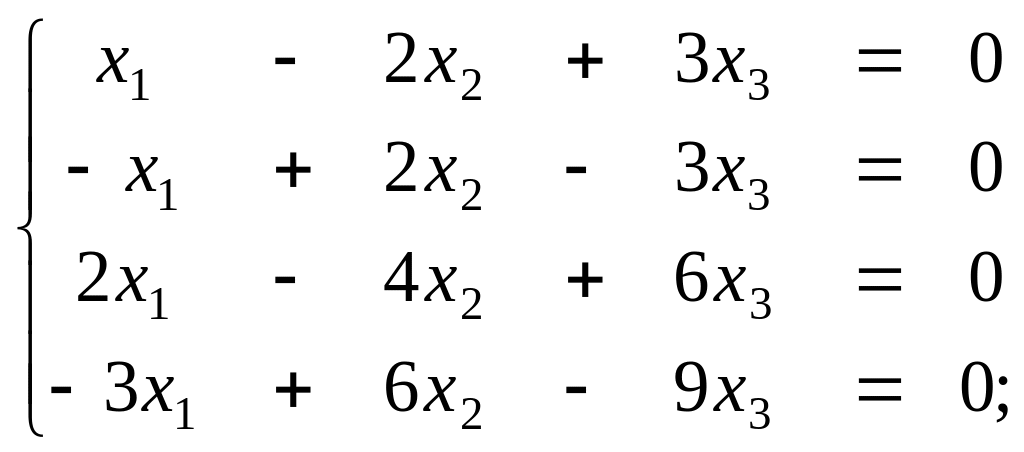
и)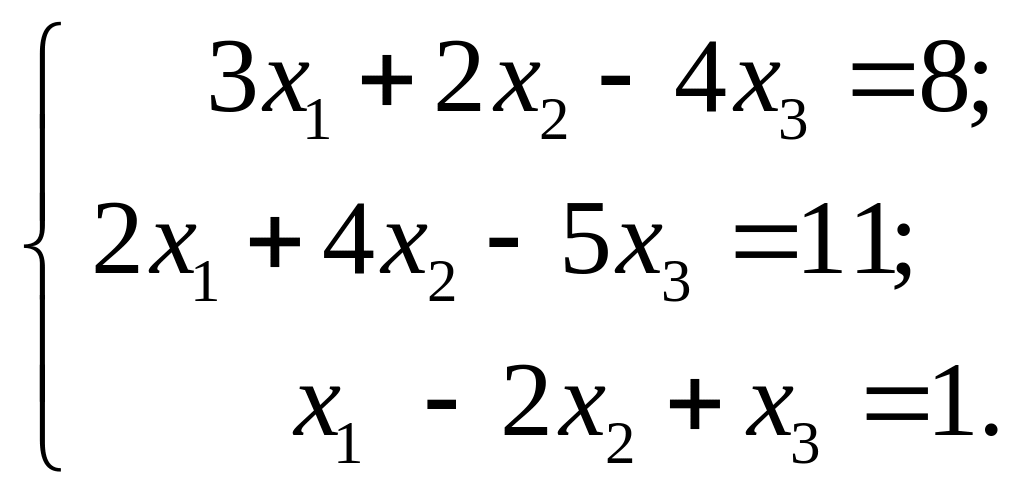 к)
к)
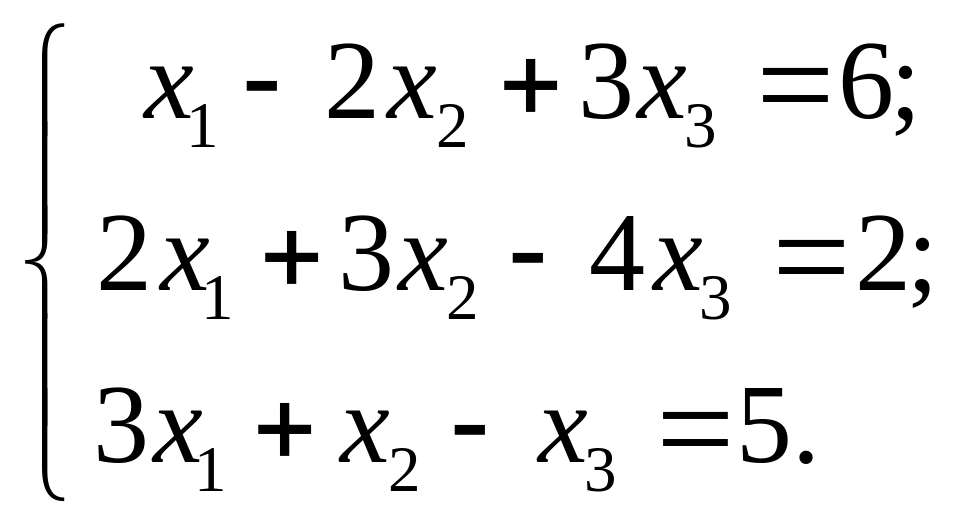
Даны точки:
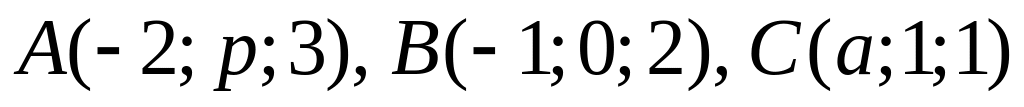 .
При каких значениях
.
При каких значениях
 и
и
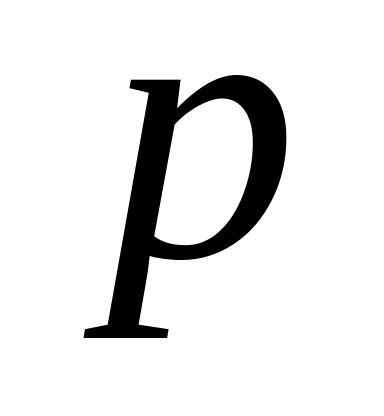 векторы
векторы
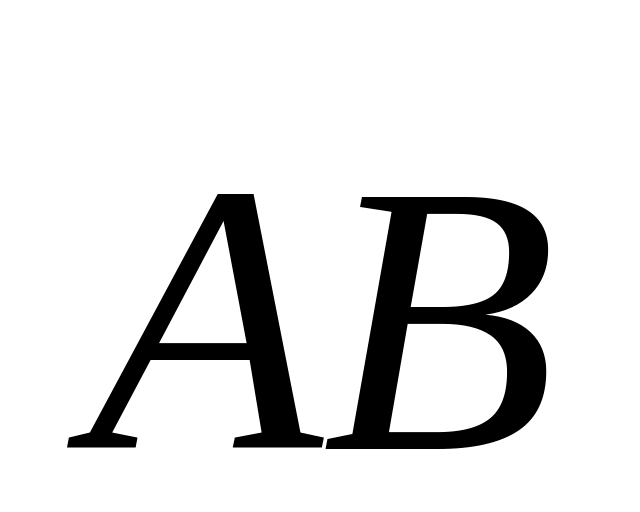 и
и
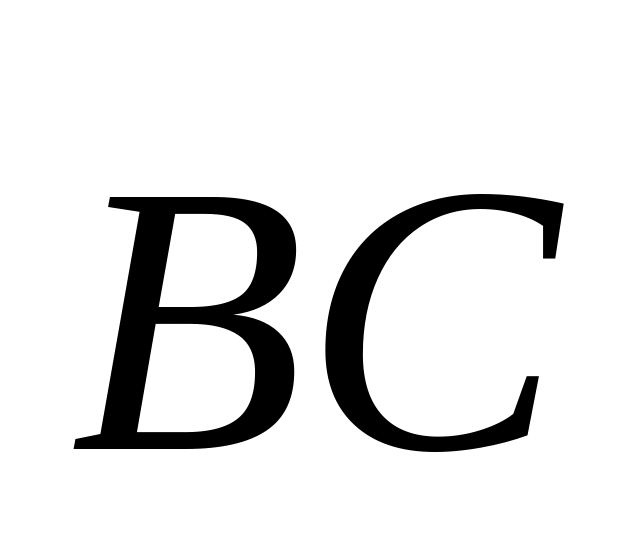 равны?
равны?Найти вектор
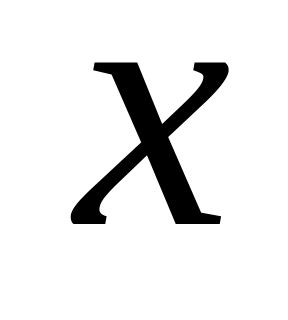 из уравнения
из уравнения
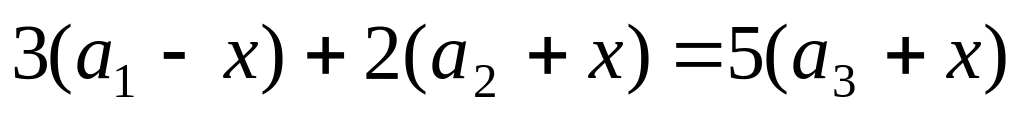 ,
если
,
если
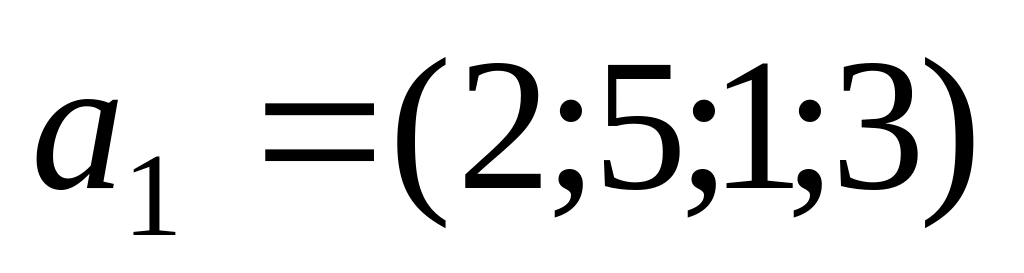 ,
,
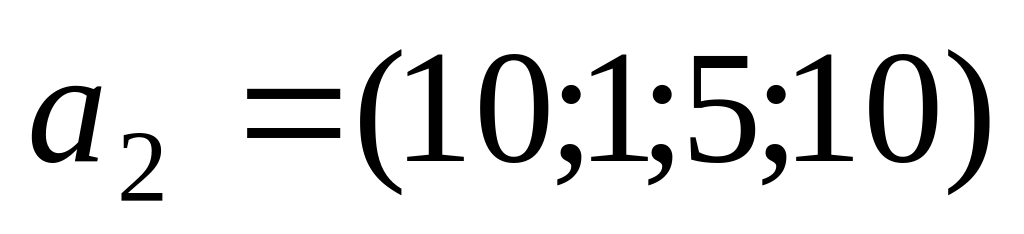 ,
,
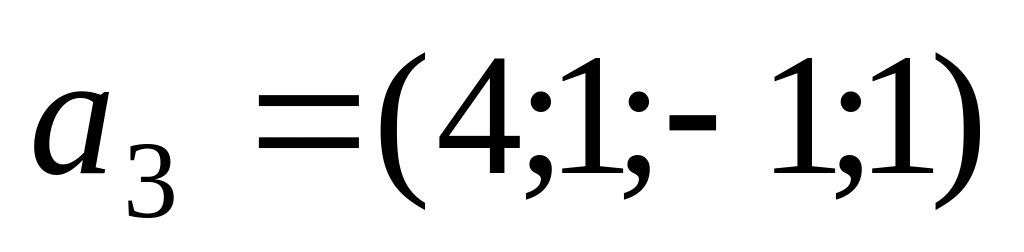 .
.Заданы пары векторов: 1).
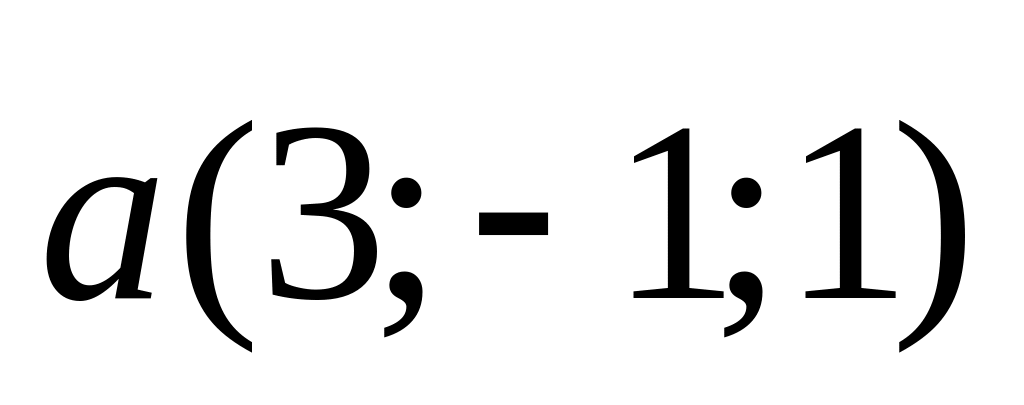 и
и
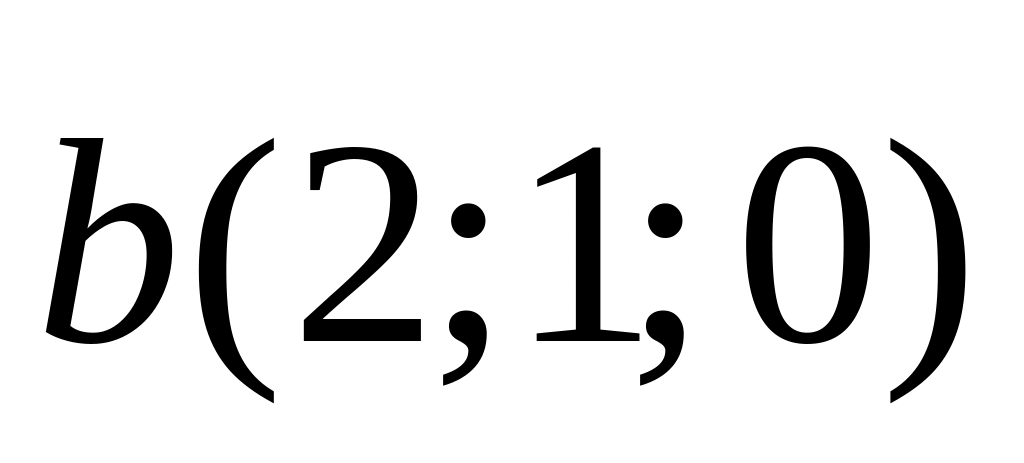 ;
2).
;
2).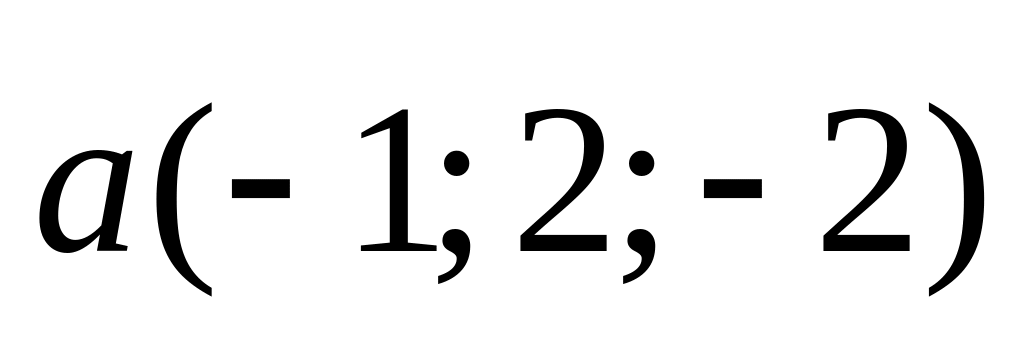 и
и
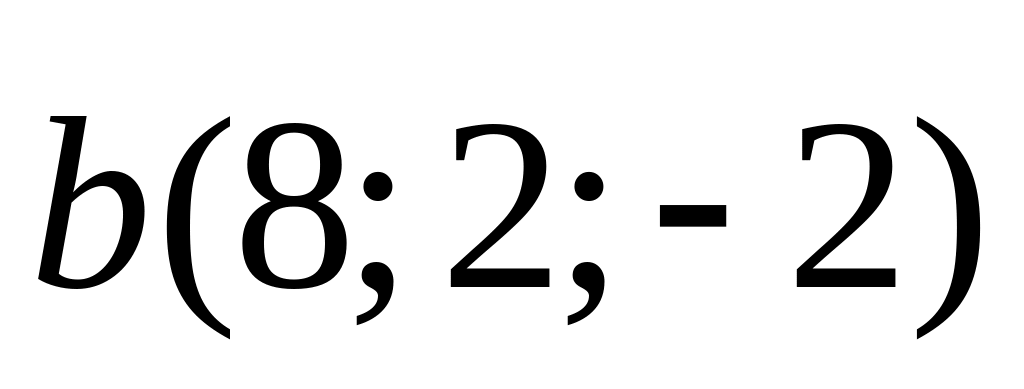 ;
3).
;
3).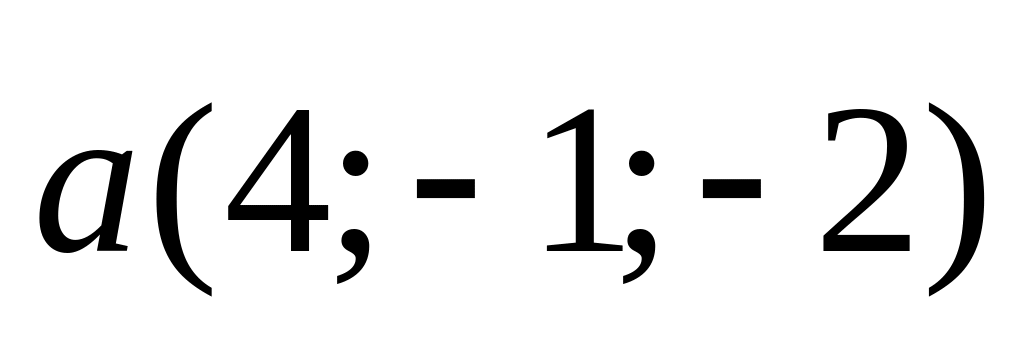 и
и
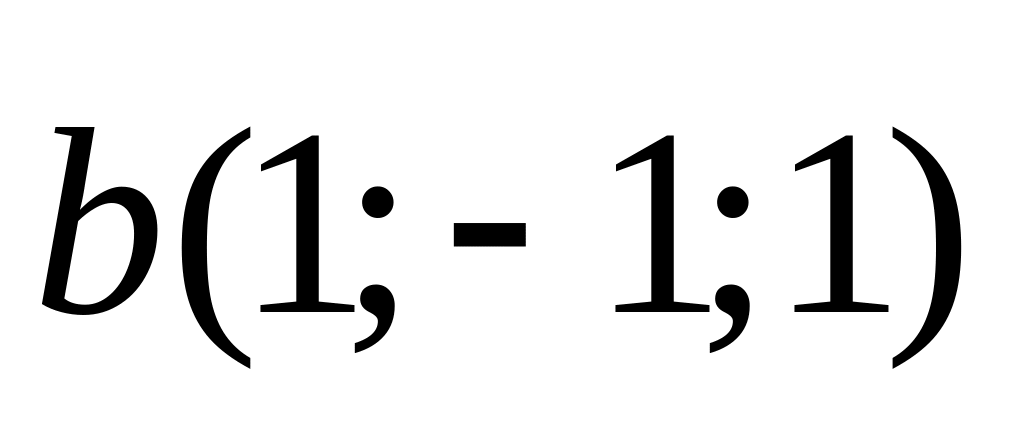 ;
4).
;
4).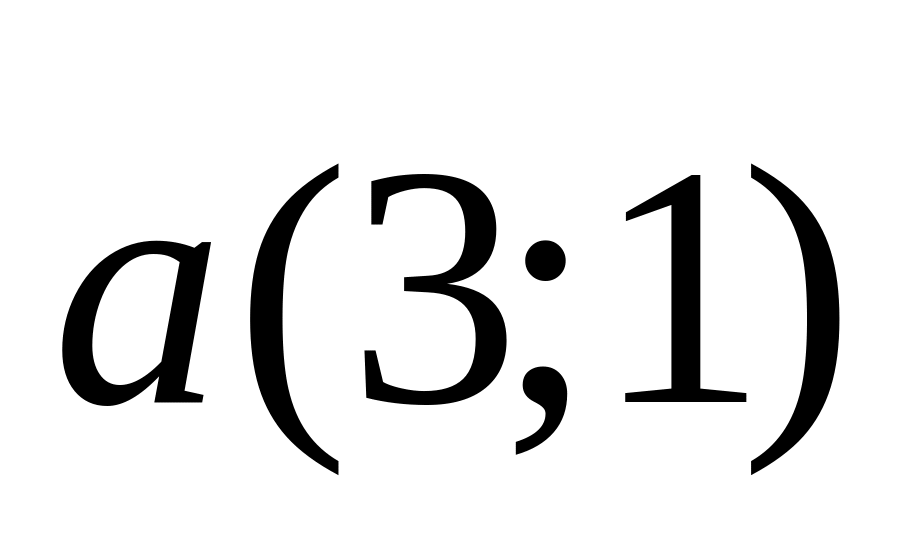 и
и
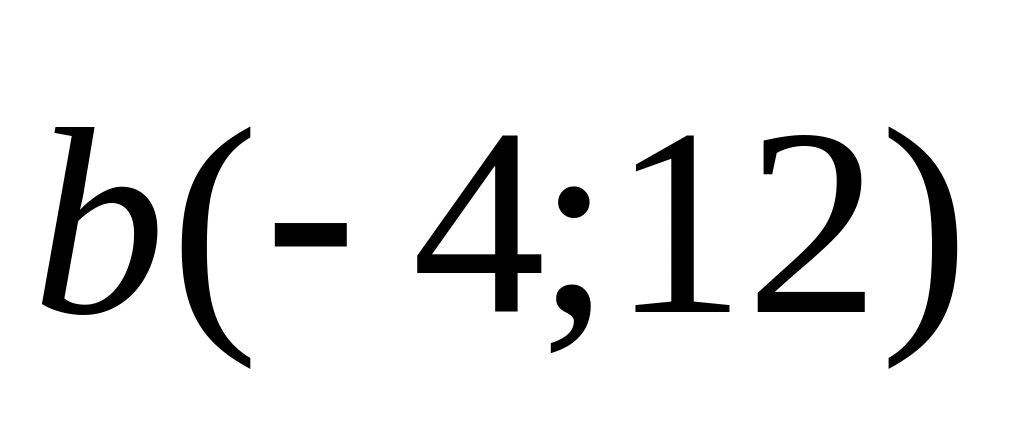 ;
5).
;
5).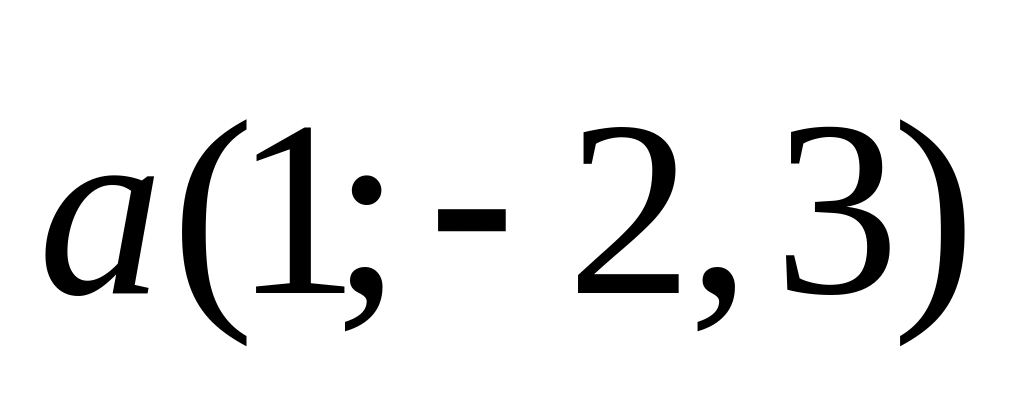 и
и
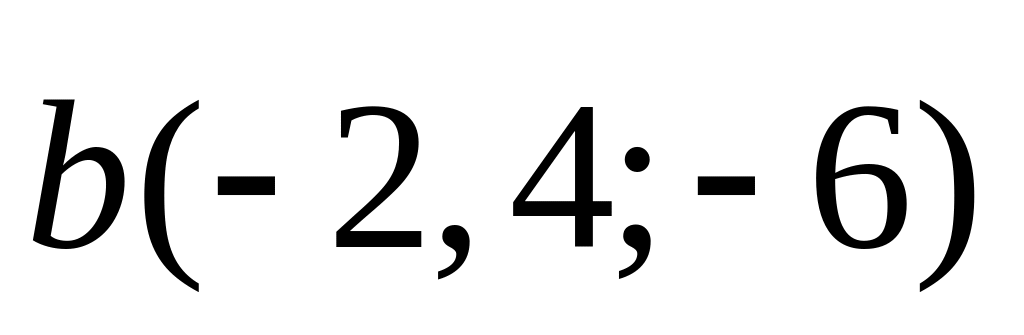 ;
6).
;
6).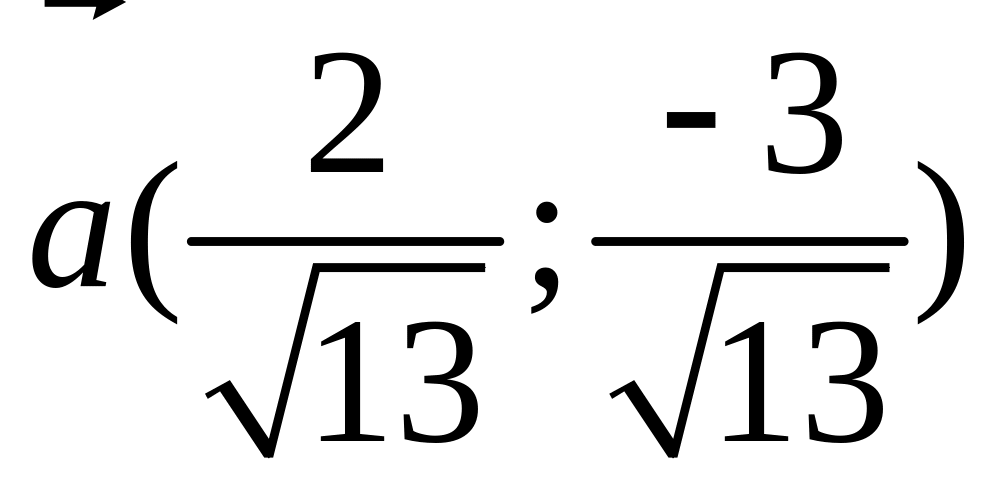 и
и
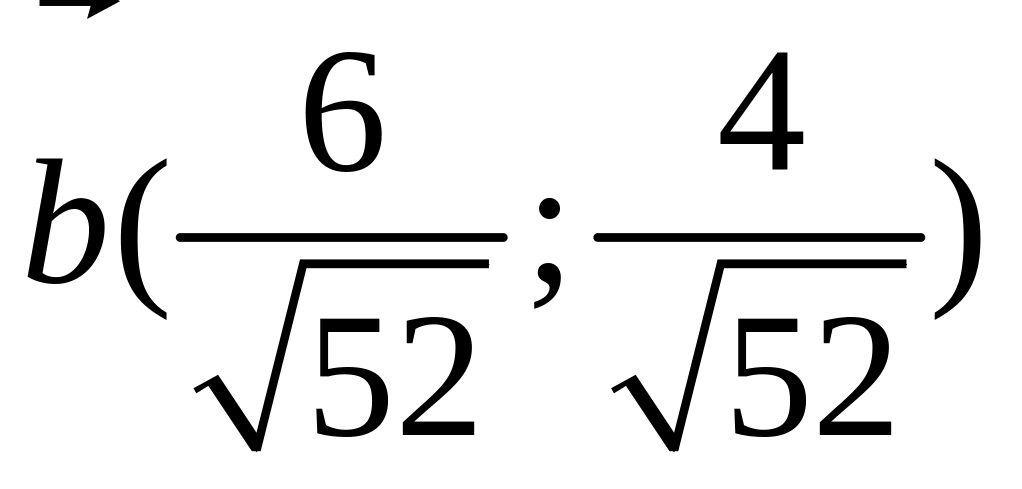 ;
7).
;
7).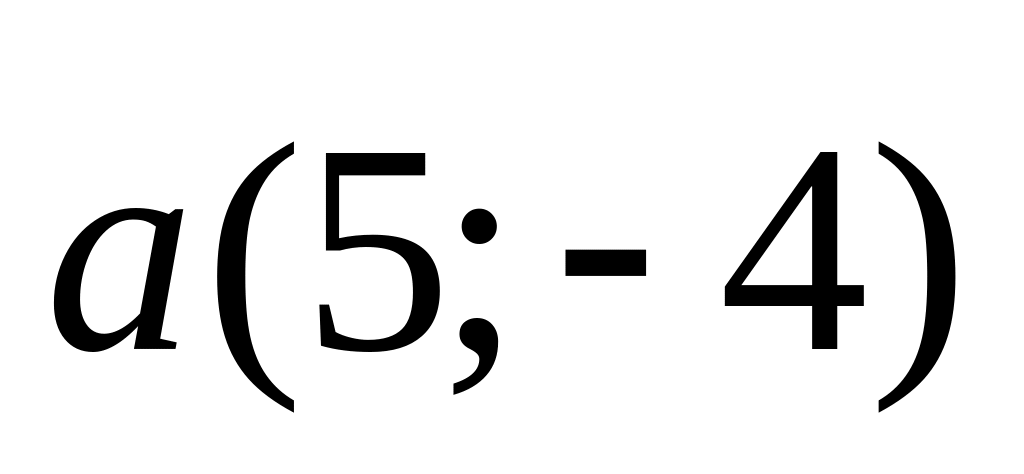 и
и
 .
Среди этих пар укажите те, которые
удовлетворяют следующим условиям: а)
.
Среди этих пар укажите те, которые
удовлетворяют следующим условиям: а)
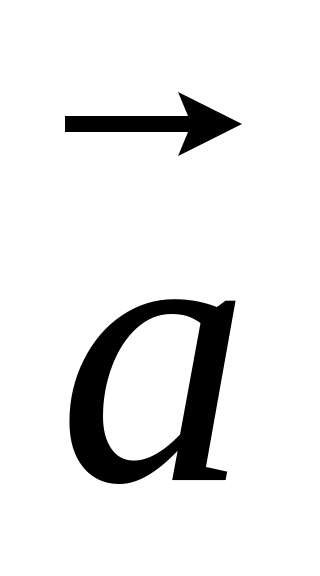 и
и
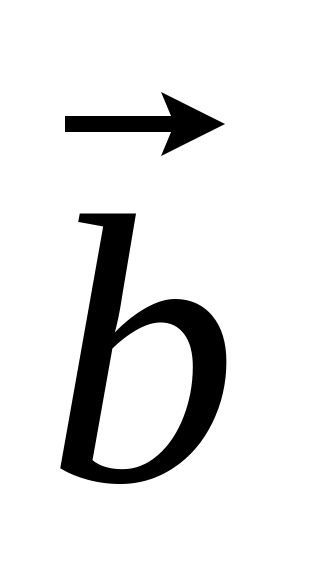 коллинеарные; б) длина вектора
равна
коллинеарные; б) длина вектора
равна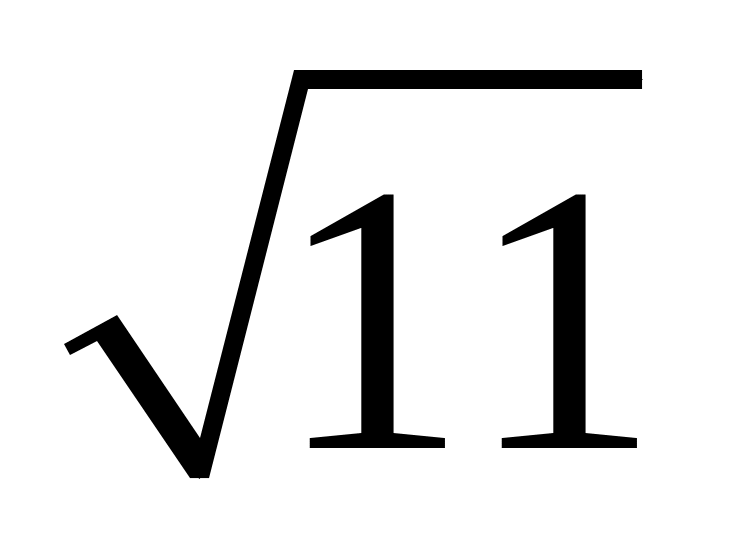 ,
длина вектора
равна
,
длина вектора
равна
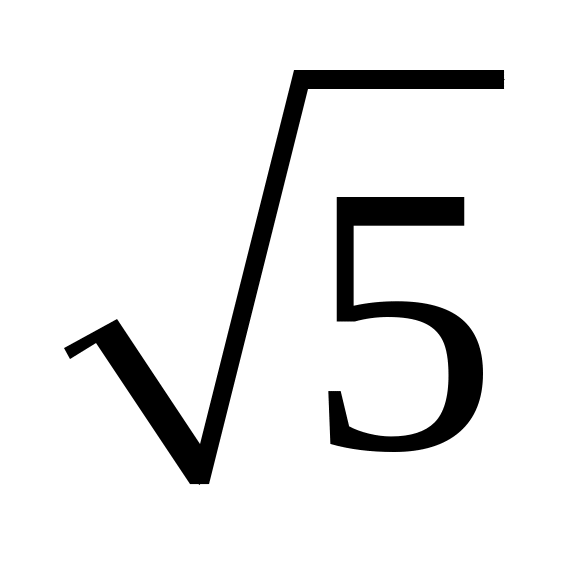 ;
в) скалярное произведение векторов
и
равно
5; г) косинус угла между векторами
;
в) скалярное произведение векторов
и
равно
5; г) косинус угла между векторами
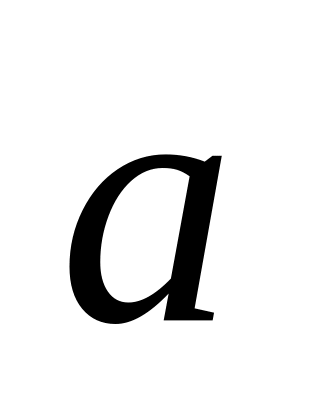 и
и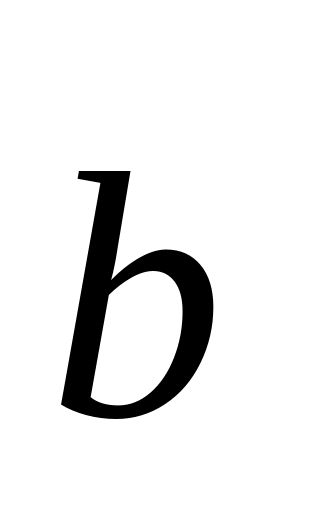 равен
равен
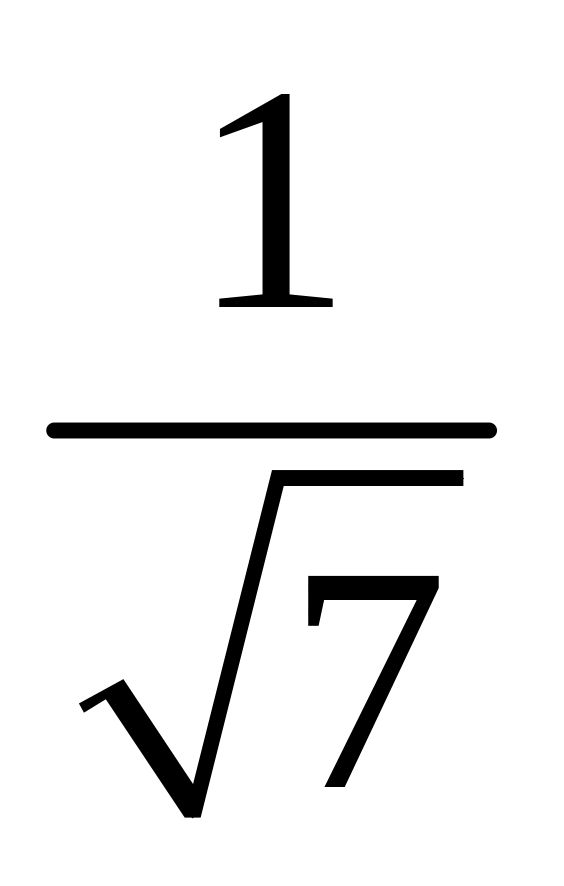 ;
д) угол между векторами
и
равен
;
д) угол между векторами
и
равен
 ;
е) векторы
и
сонаправлены;
ж) векторы
и
ортогональны.
;
е) векторы
и
сонаправлены;
ж) векторы
и
ортогональны.Даны два вектора
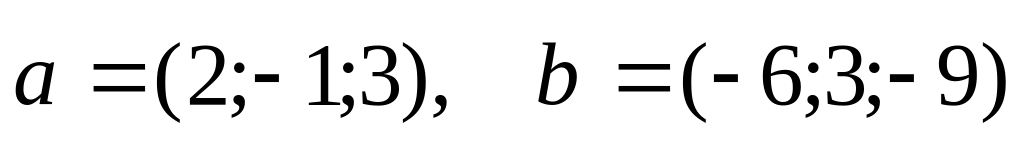 .
Проверить, что векторы
и
коллинеарные. Установить, во сколько
раз один длиннее второго и как они
направлены – в одну сторону или в
противоположные стороны.
.
Проверить, что векторы
и
коллинеарные. Установить, во сколько
раз один длиннее второго и как они
направлены – в одну сторону или в
противоположные стороны.Даны точки
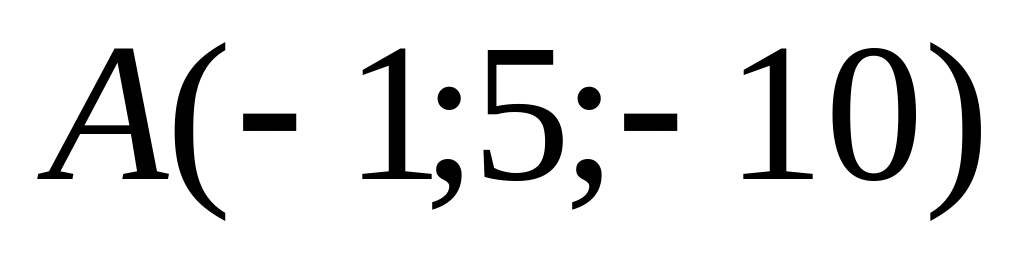 ,
,
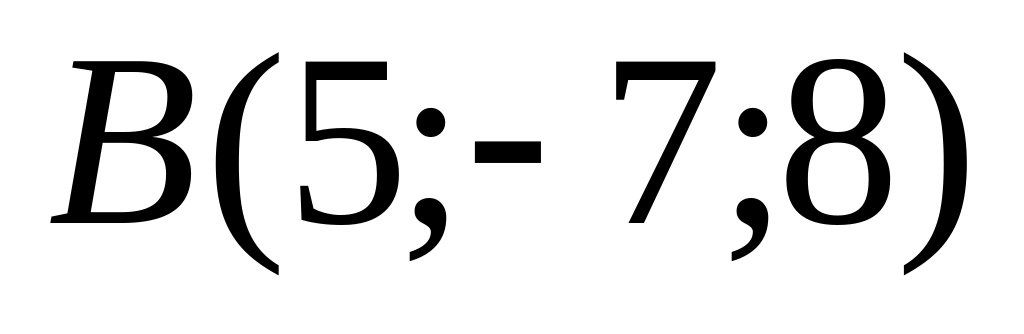 ,
,
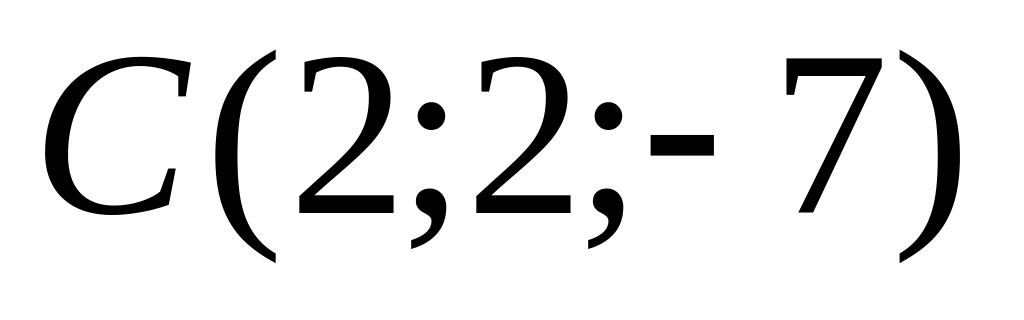 и
и
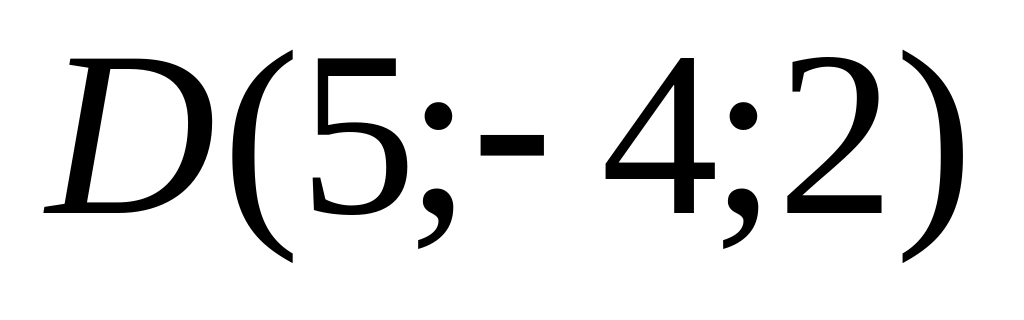 .
Проверить, что векторы
.
Проверить, что векторы
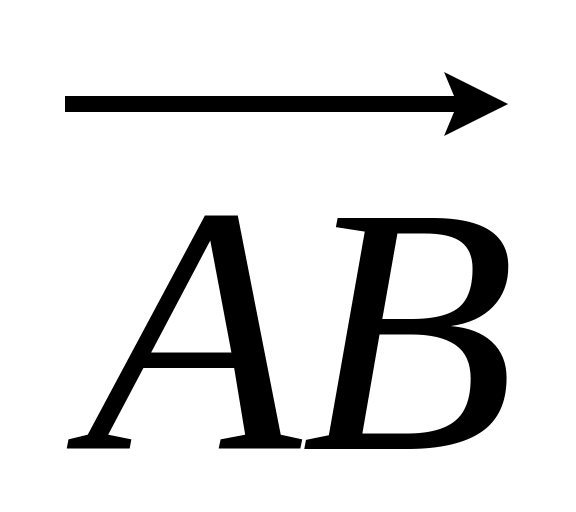 и
и
 коллинеарные. Установить, во сколько
раз один длиннее второго.
коллинеарные. Установить, во сколько
раз один длиннее второго.Даны векторы
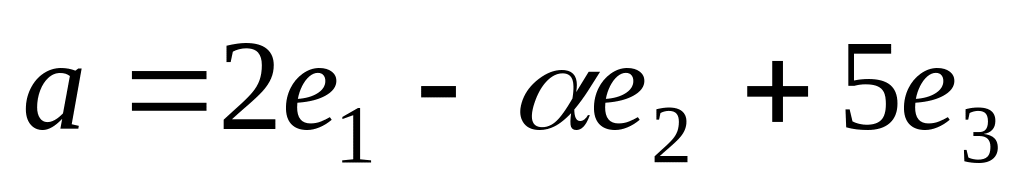 и
и
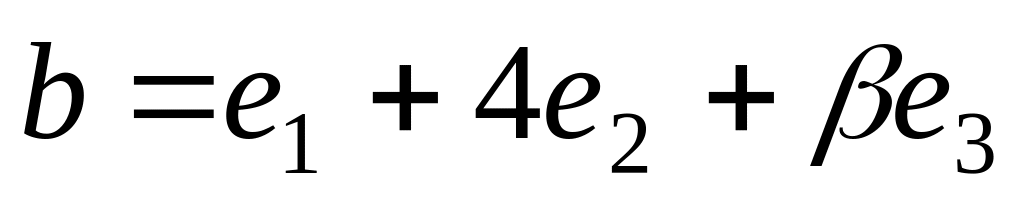 ,
где
,
где
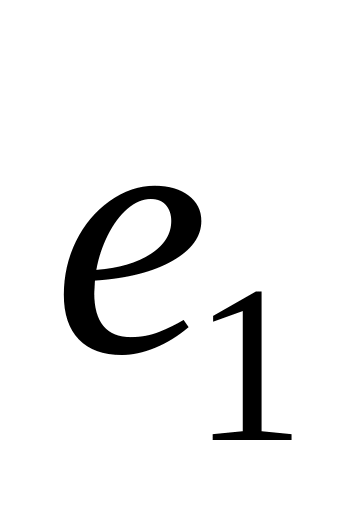 ,
,
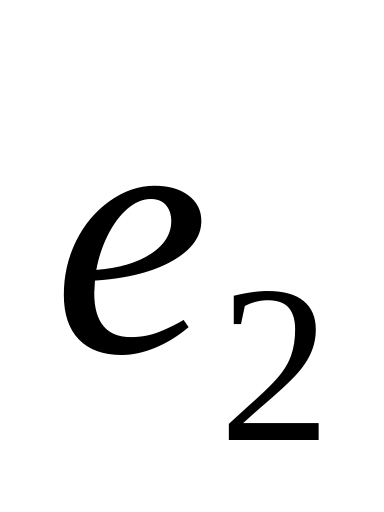 ,
,
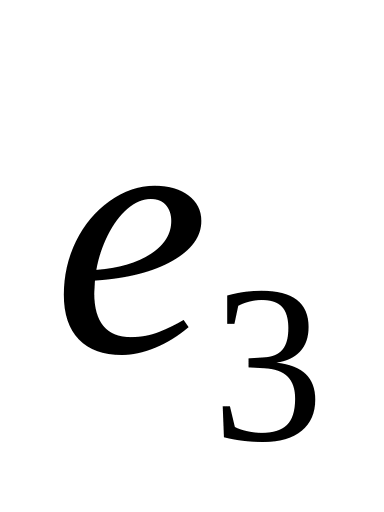 — базис. При каких значениях
— базис. При каких значениях
 и
и
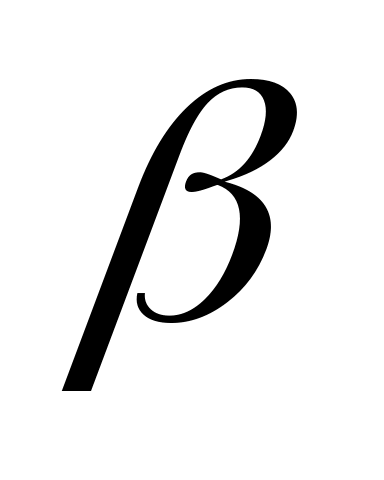 векторы
векторы
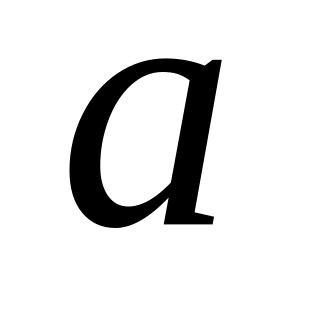 и
и
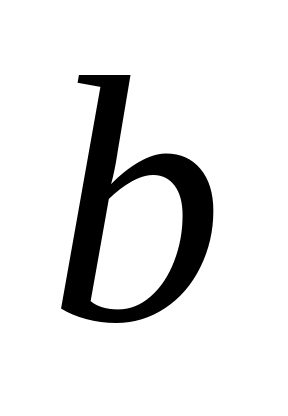 коллинеарные?
коллинеарные?Дано разложение вектора
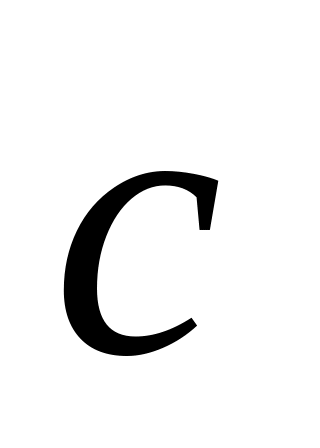 по
базису
по
базису
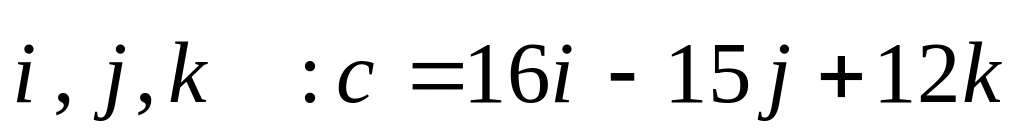 .
Разложить вектор
.
Разложить вектор
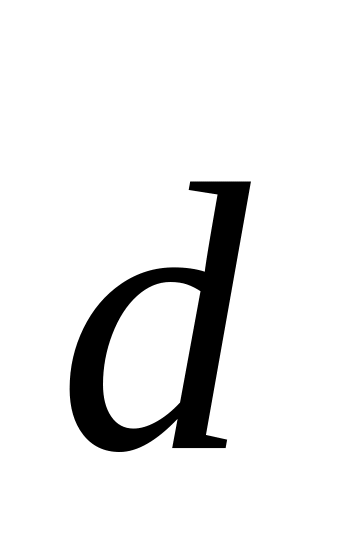 по
этому базису, если эти векторы коллинеарные
и противоположно направлены, а
по
этому базису, если эти векторы коллинеарные
и противоположно направлены, а
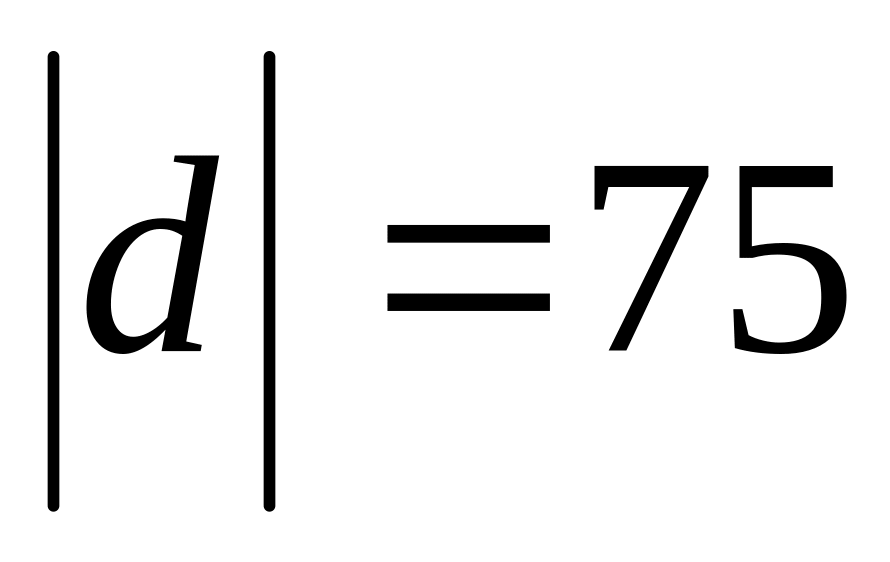 .
.
Вычислить скалярное произведение
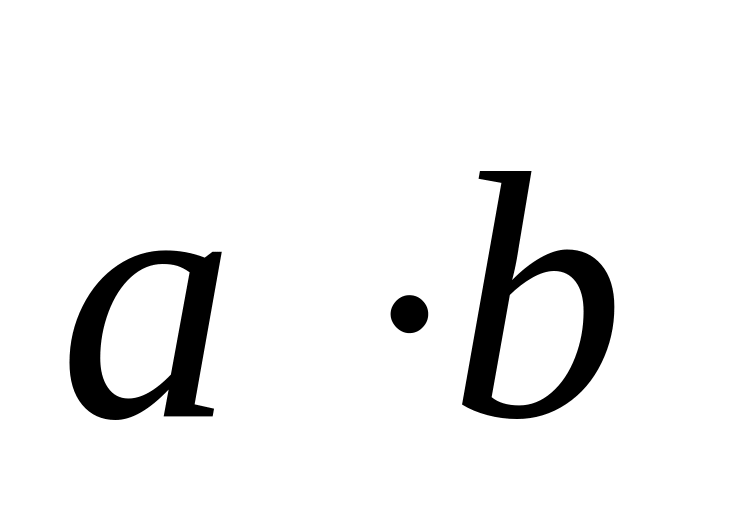 :
:1).
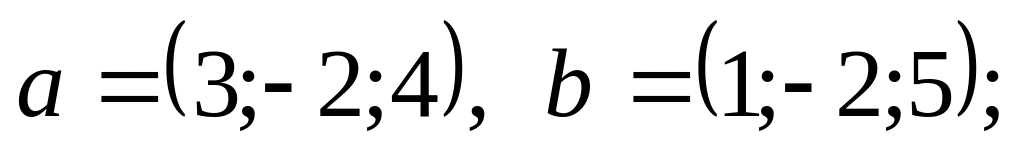
2).
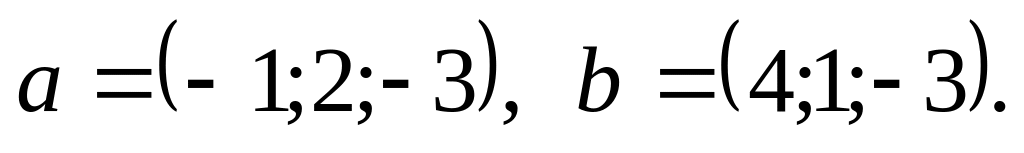
3).
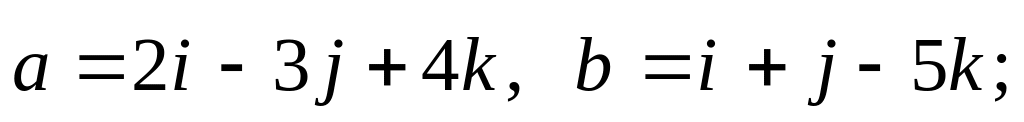
4).
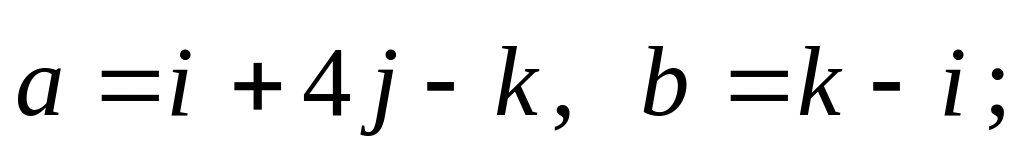
Найти косинус угла между векторами и
-
1).
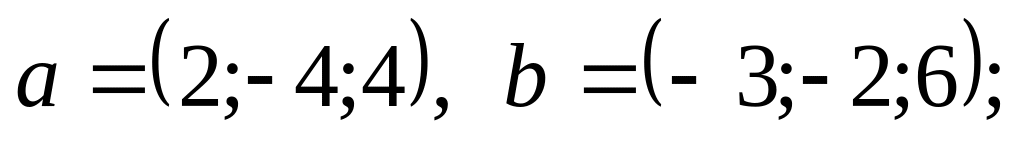
2).
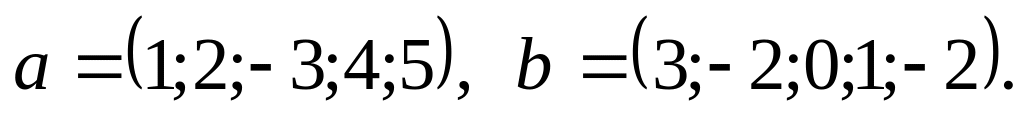
3).
4).
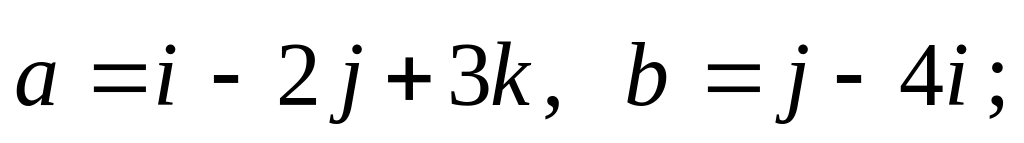
5).
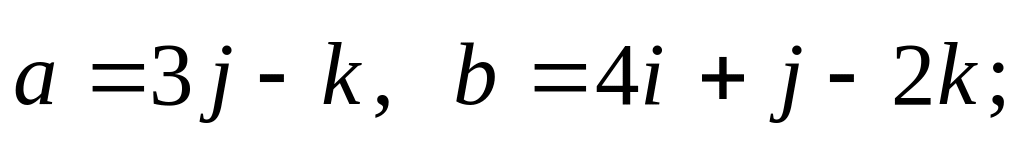
6).
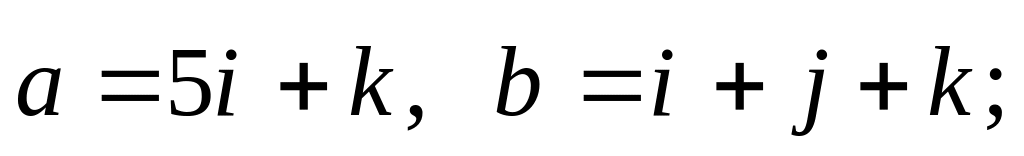
Найти единичный вектор
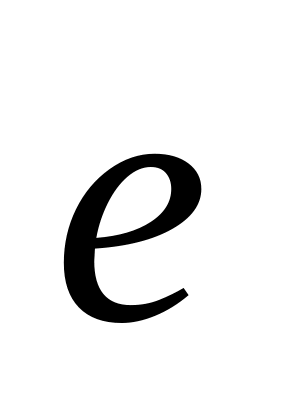 ,
направление которого совпадает с
направлением вектора
,
направление которого совпадает с
направлением вектора
1).
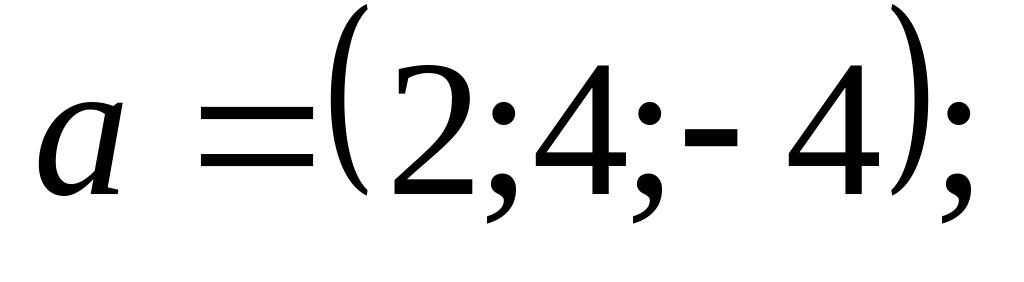
2).
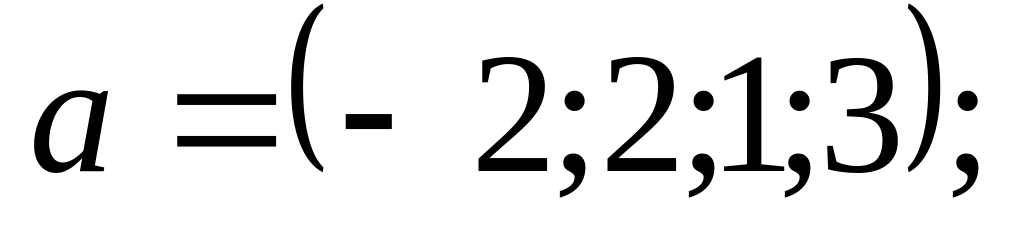
3).
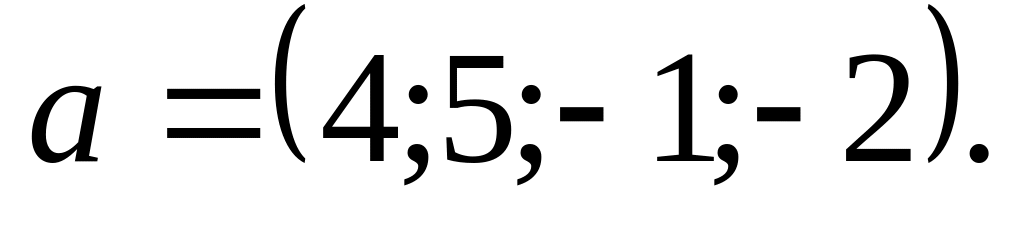
Найти единичный вектор, направленный противоположно вектору 1)
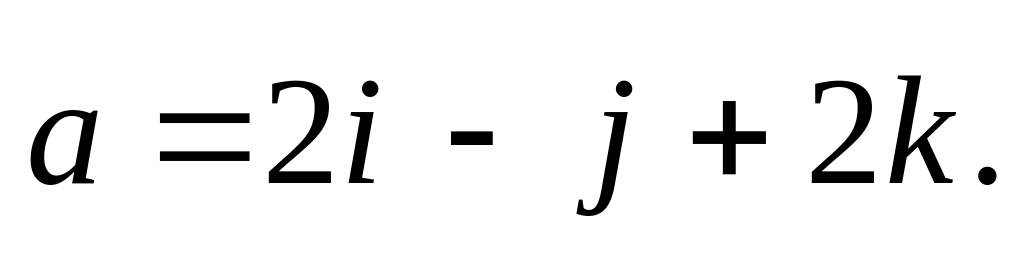 2)
2)
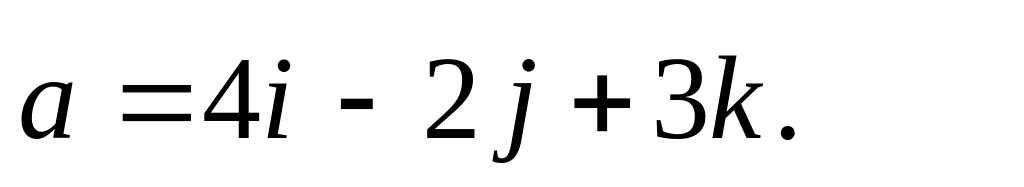
На векторах 1)
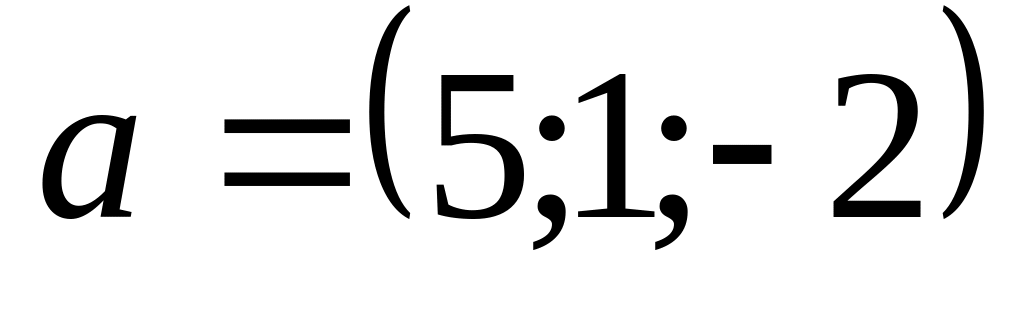 и
и
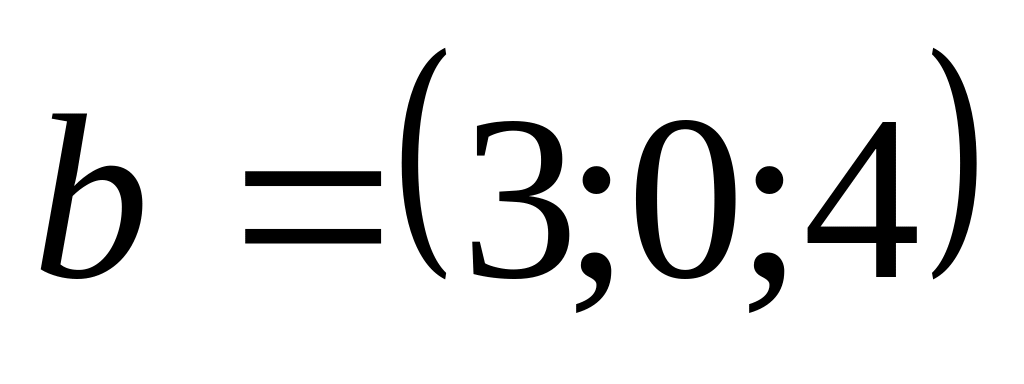 2)
2)
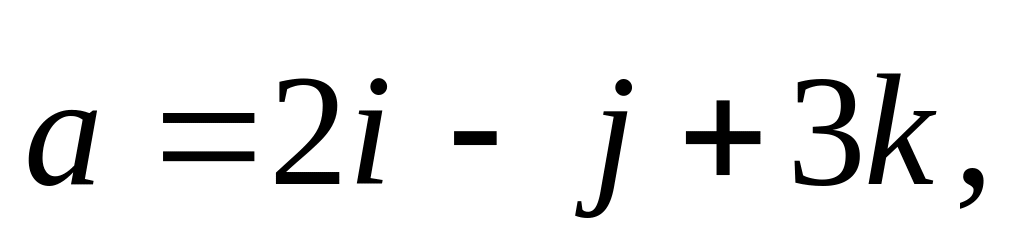
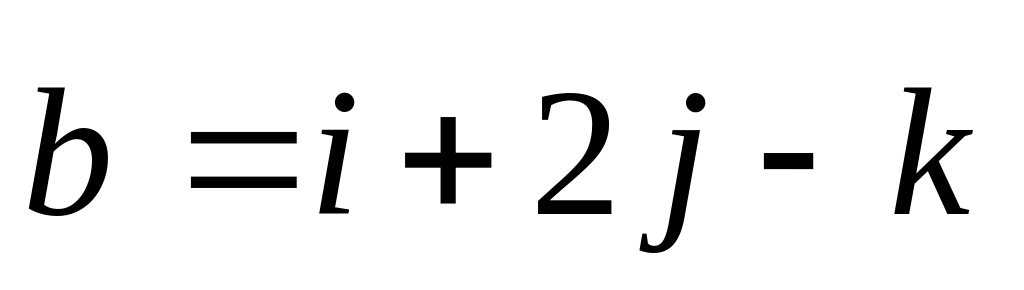 Построен параллелограмм. Записать
векторы, направленные вдоль его
диагоналей.
Построен параллелограмм. Записать
векторы, направленные вдоль его
диагоналей.Являются ли коллинеарными векторы и заданные координатами в некотором базисе:
1).
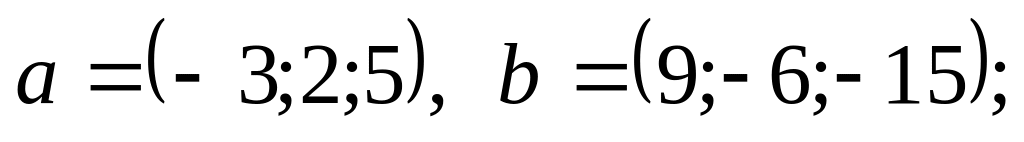
2).
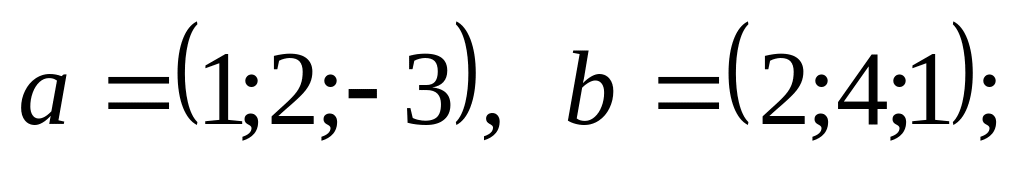
3).
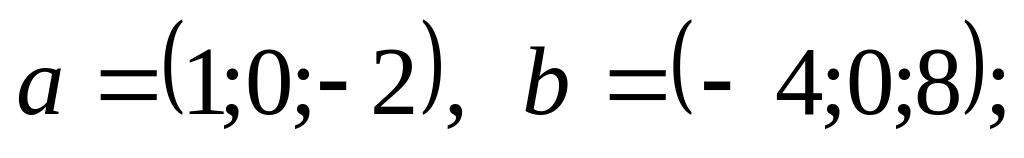
4).
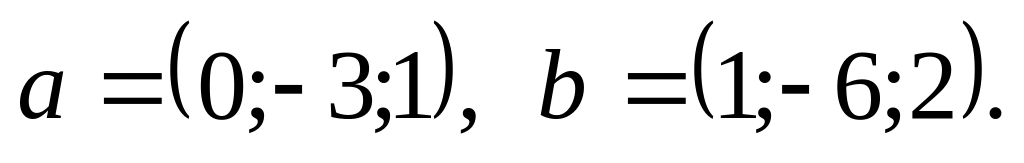
Являются ли ортогональными векторы и заданные координатами в некотором базисе:
1).
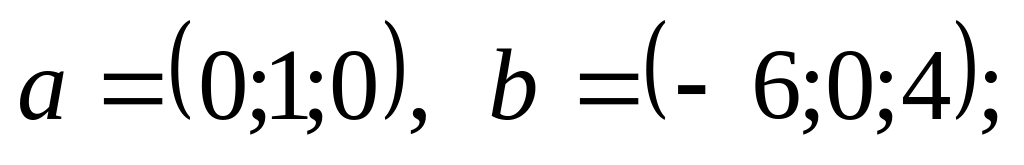
2).
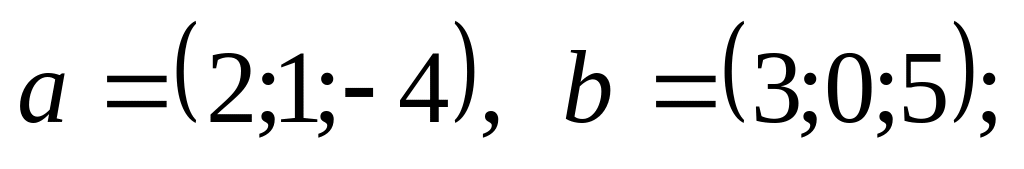
3).
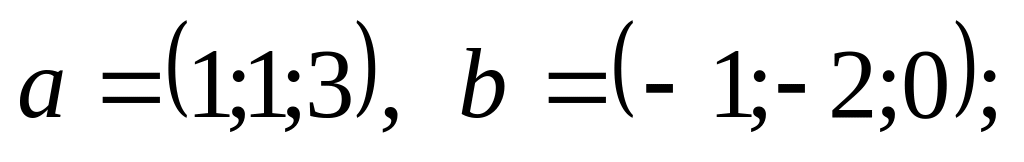
4).
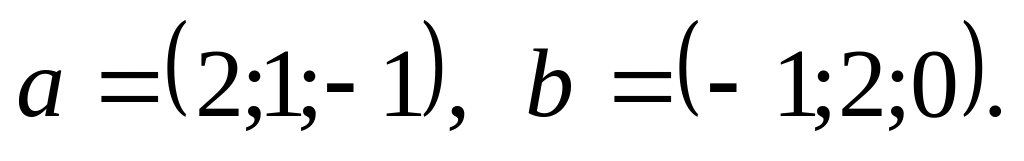
Даны точки
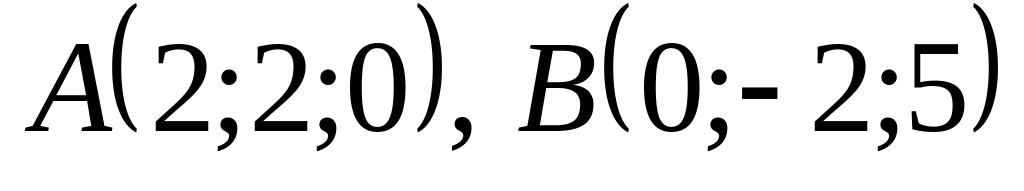 .
Определить длину вектора
.
Определить длину вектора
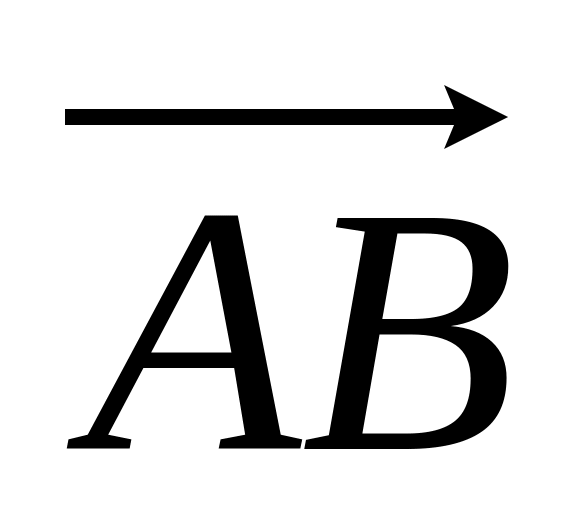 .
.Даны векторы
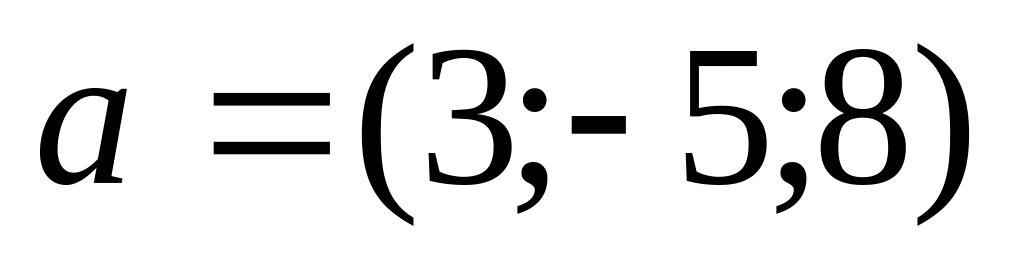 и
и
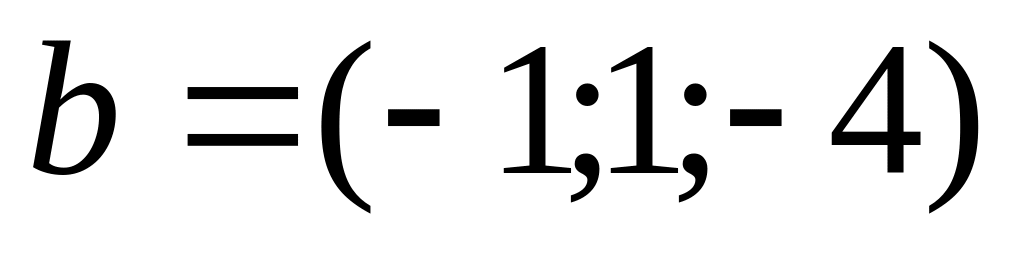 .
Найти
.
Найти
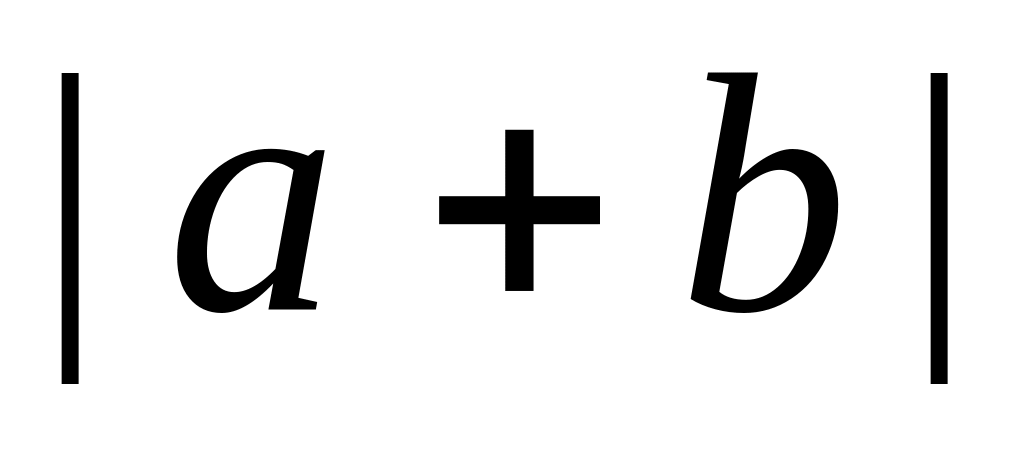 и
и
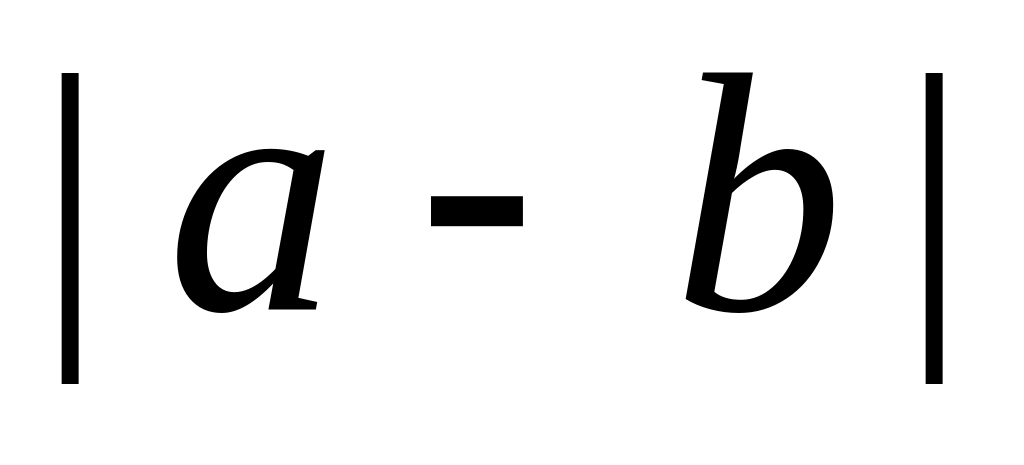 .
.Даны векторы: а)
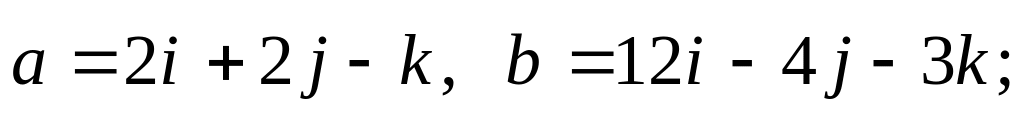 б)
б)
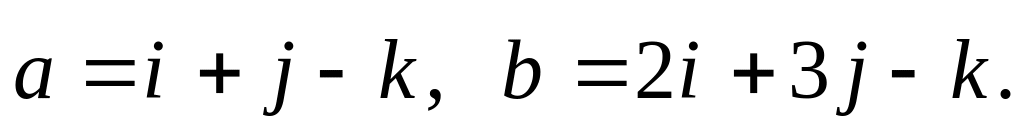 Определить
длины векторов и косинус угла между
ними.
Определить
длины векторов и косинус угла между
ними.Даны векторы:
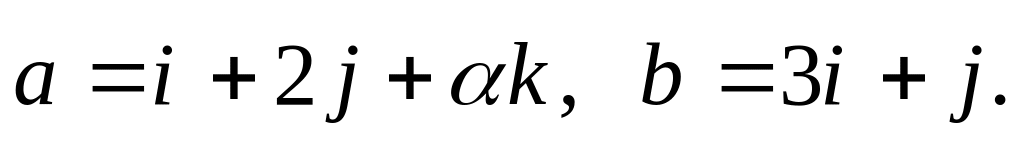 При
каком значении
При
каком значении
 косинус угла между ними будет равен
5/12?
косинус угла между ними будет равен
5/12?Даны точки
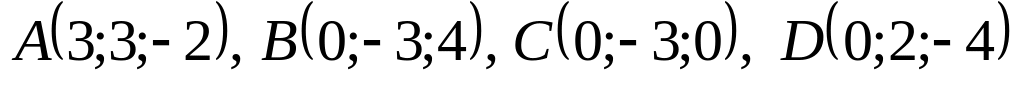 .
Найти скалярное произведение
и
.
Найти скалярное произведение
и
 .
.Даны векторы
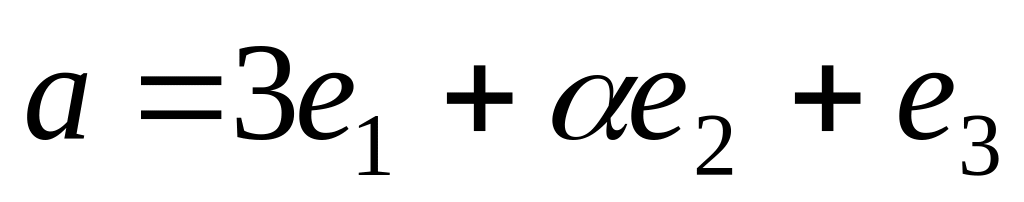 и
и
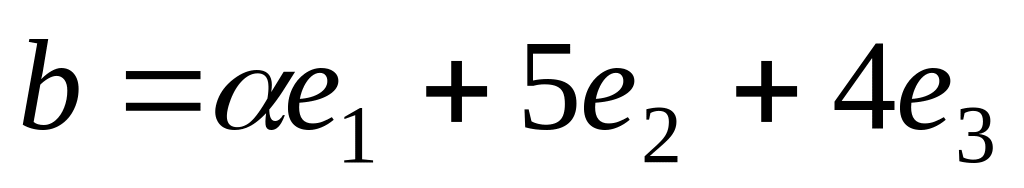 в базисе
,
,
.
При каком значении
они ортогональны?
в базисе
,
,
.
При каком значении
они ортогональны?Даны вершины четырехугольника A(1;-2;2), B(1;4;0), C(-4;1;1), D(-5;-5;3). Доказать, что диагонали взаимно перпендикулярны.
Даны точки А1(0;1;2), А2(1;2;4), B1(-1;-1;3), B2(1;0;0). Найти координаты вектора
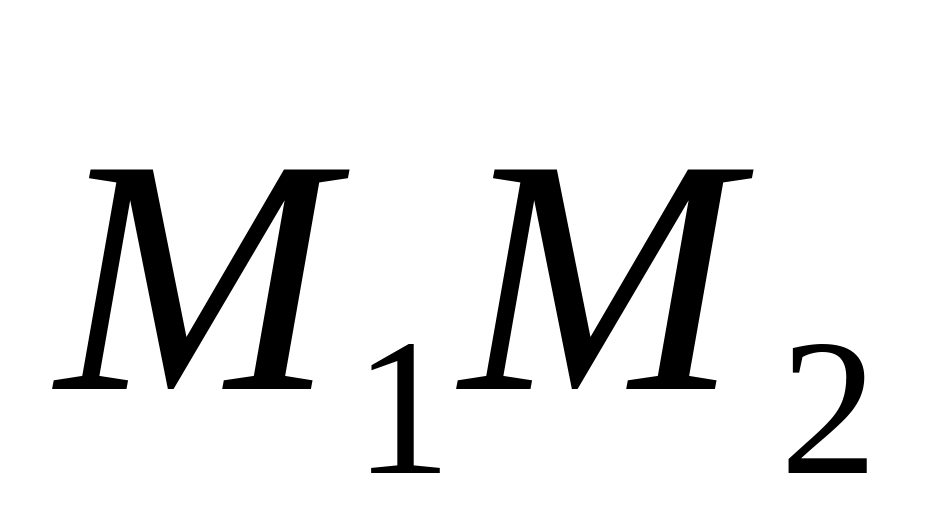 и
и
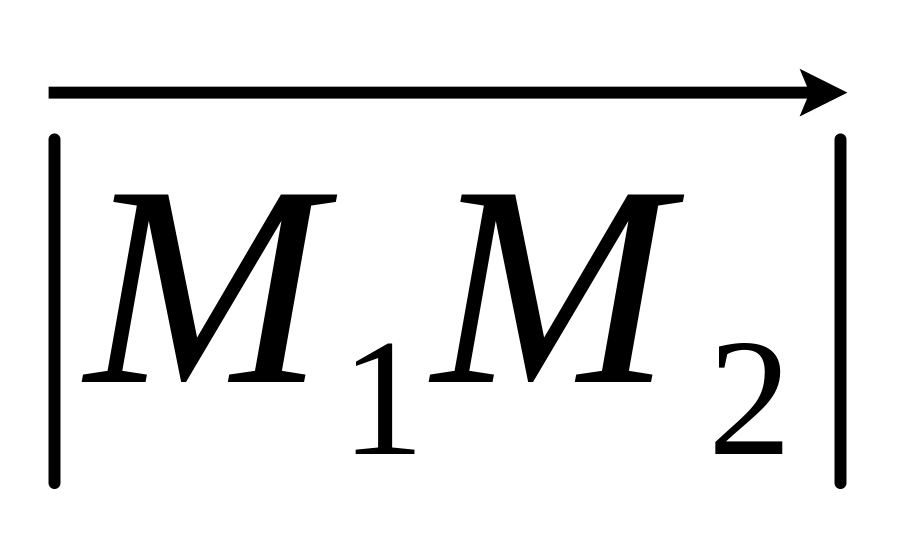 ,
если точки M1
и M2
–середины отрезков A1
B1
A2
B2
соответственно.
,
если точки M1
и M2
–середины отрезков A1
B1
A2
B2
соответственно.Даны точки A(-1;2;3), B(-1;3;1), C(-1;7;3), D(-1;6;5). Доказать, что ABCD – прямоугольник.
Дан треугольник с вершинами
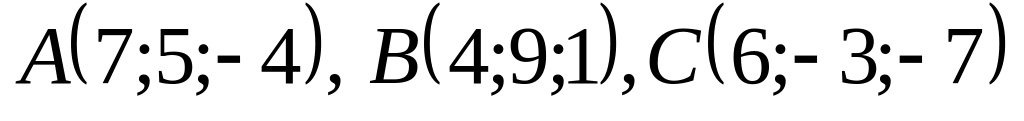 .
Найти векторы, совпадающие с его
сторонами и вычислить его периметр.
.
Найти векторы, совпадающие с его
сторонами и вычислить его периметр.Проверить, будет ли треугольник с вершинами A(6;-4;2), B(3;2;3), C(3;-5;-1) прямоугольным?
Даны точки A(-3;-2;0), B(3;3;1), C(5;0;2). Во сколько раз
 больше (меньше)
больше (меньше)
 ?
?На векторах
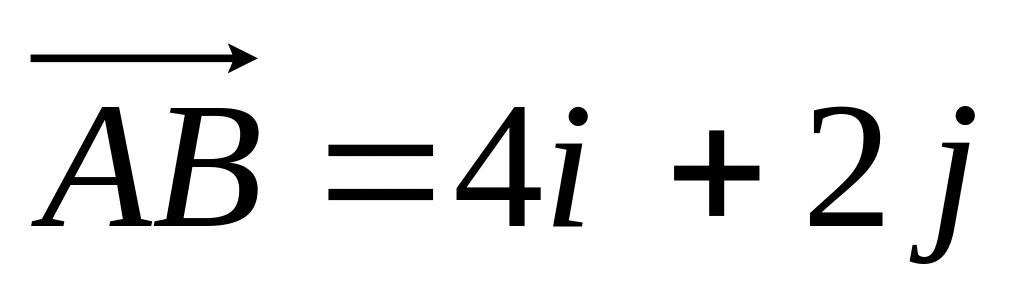 и
и
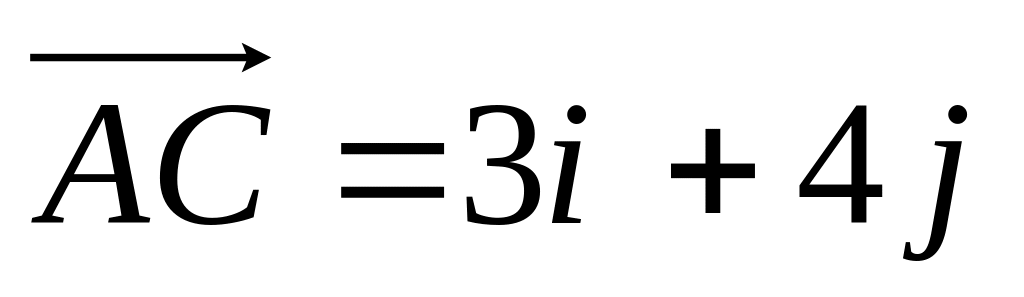 построен
треугольник. Доказать, что треугольник
прямоугольный и найти его площадь.
построен
треугольник. Доказать, что треугольник
прямоугольный и найти его площадь.При каком значении
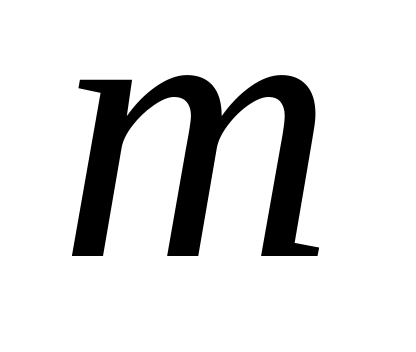 векторы
векторы
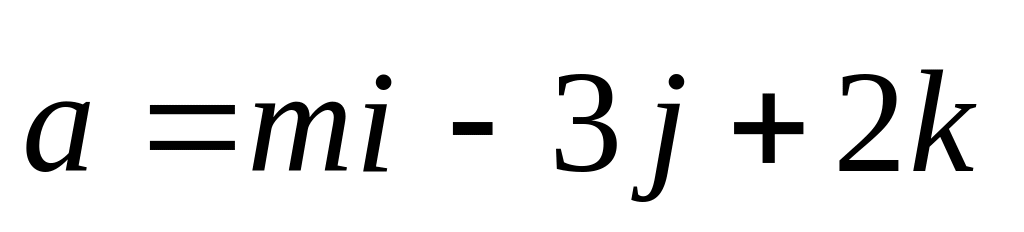 и
и
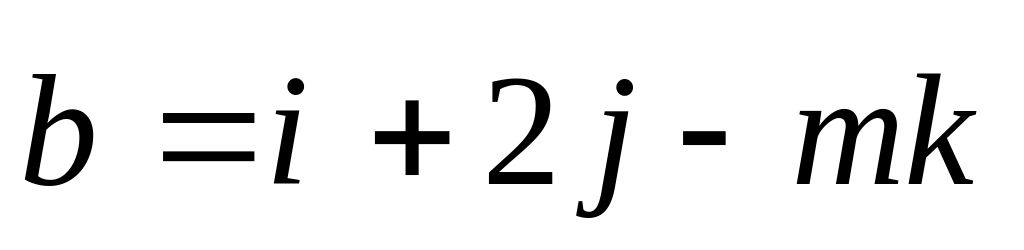 взаимно
перпендикулярны?
взаимно
перпендикулярны?Дан вектор
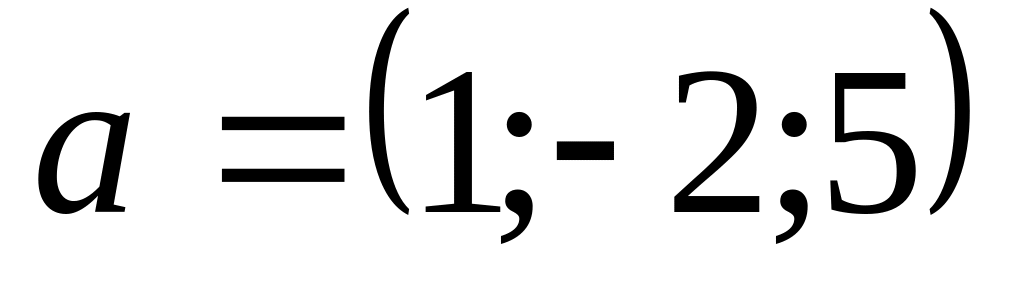 .
Найти координаты вектора
.
Найти координаты вектора
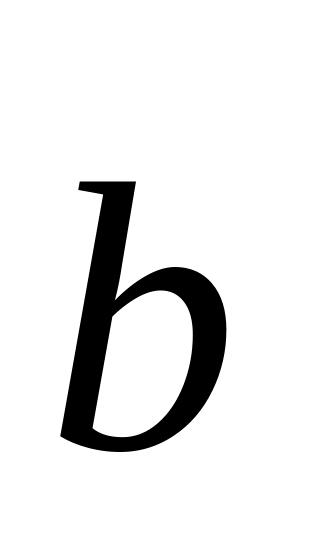 ,
лежащего в плоскости Oxy
, если
,
лежащего в плоскости Oxy
, если
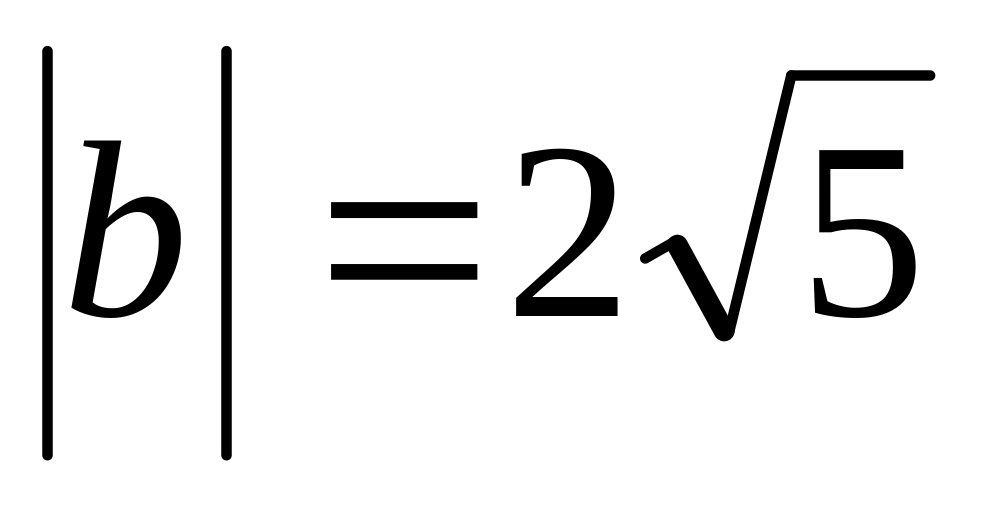 и
векторы
и
векторы
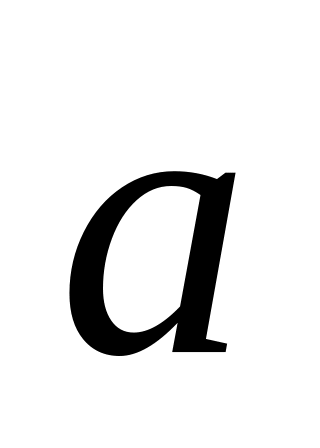 и
перпендикулярны.
и
перпендикулярны.Даны векторы
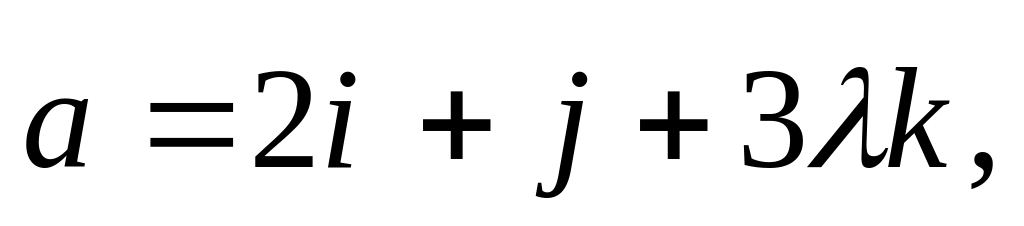
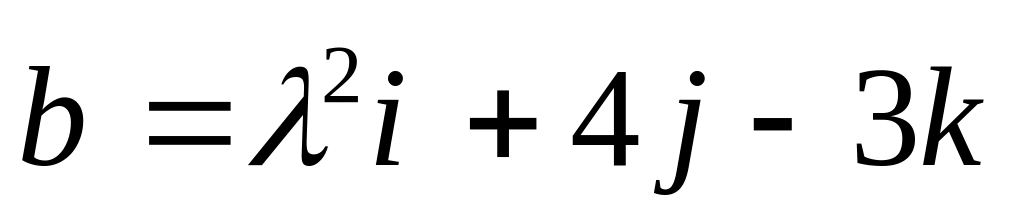 .
При каких значениях
.
При каких значениях
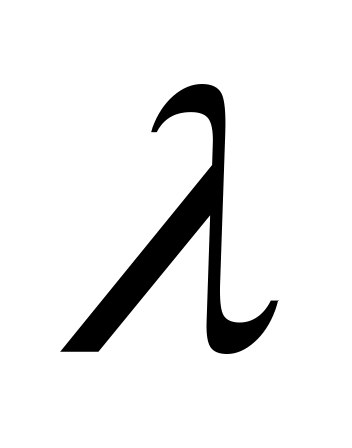 векторы
и
перпендикулярны?
векторы
и
перпендикулярны?Даны точки M(1;1;4), N(1;4;4), K(3;3;2). Доказать, что векторы
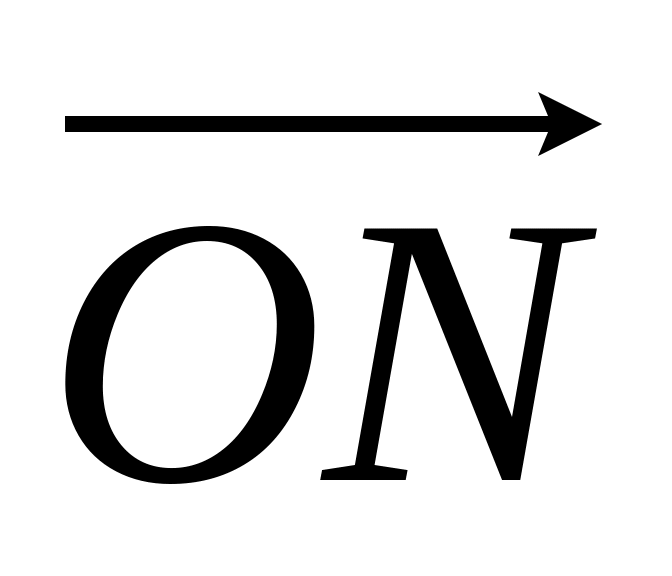 и
и
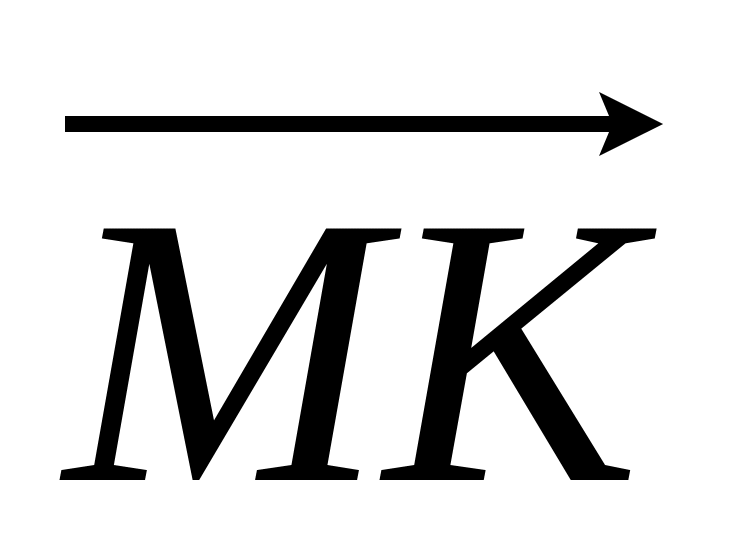 перпендикулярны,
если точка O
– середина отрезка MK.
перпендикулярны,
если точка O
– середина отрезка MK.Найти угол между векторами
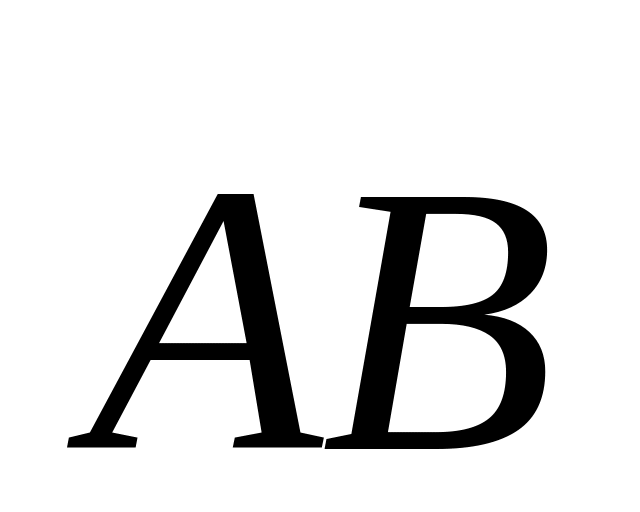 и
и
 ,
если A(3;3;-2),
B(0;-3;4),
C(0;-3;0),
D(0;2;-4).
,
если A(3;3;-2),
B(0;-3;4),
C(0;-3;0),
D(0;2;-4).На векторах
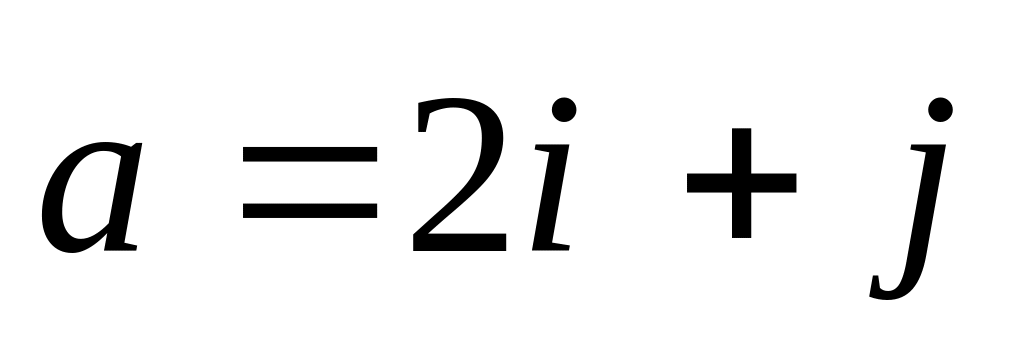 и
и
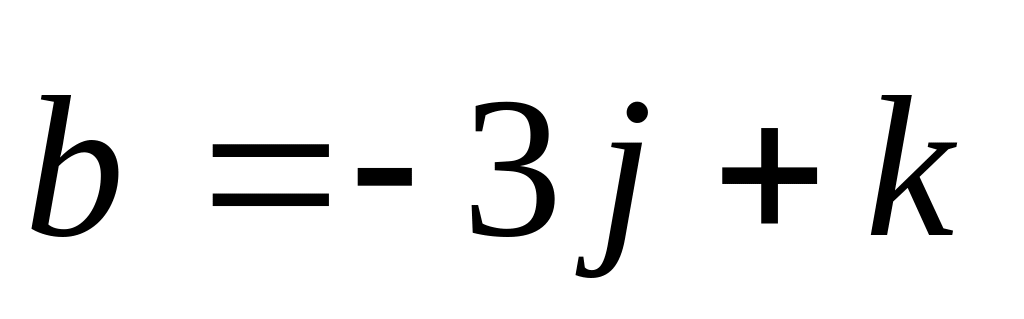 построен
параллелограмм. Вычислить длины его
диагоналей.
построен
параллелограмм. Вычислить длины его
диагоналей.Определить длины сторон параллелограмма, диагоналями которого служат векторы
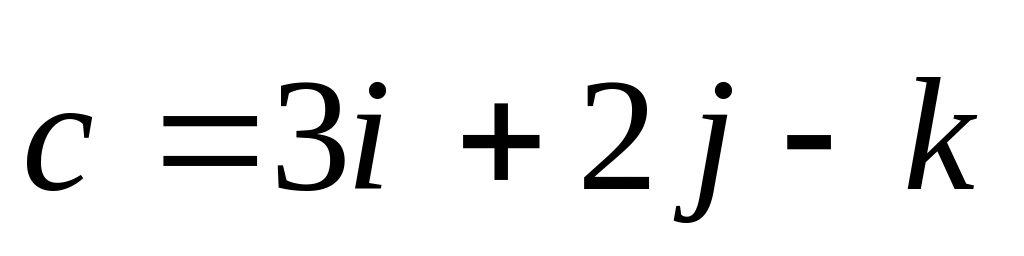 и
и
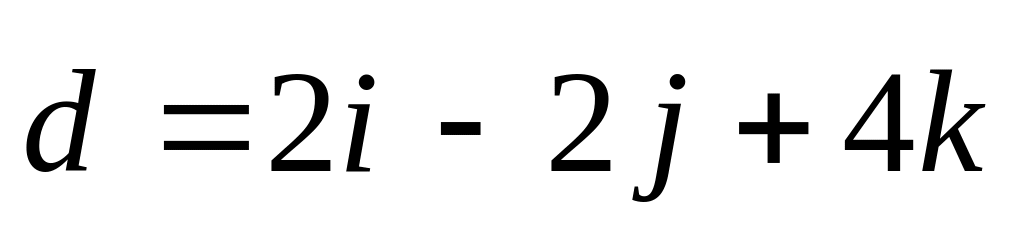 .
.Образует ли система векторов ортогональный базис? Если да, то постройте по этому ортонормированному, базису соответствующий ортогональный базис а)
 (1;1;0;-1;-1),
(1;0;-1;0;1), (1;-1;2;-1;1), (1;-1;0;1;-1).
б) (1;3;2;3;1),
(1;1;0;-1;-1), (1;0;-1;0;1), (1;-1;2;-1;1), (1;-1;0;1;-1).
(1;1;0;-1;-1),
(1;0;-1;0;1), (1;-1;2;-1;1), (1;-1;0;1;-1).
б) (1;3;2;3;1),
(1;1;0;-1;-1), (1;0;-1;0;1), (1;-1;2;-1;1), (1;-1;0;1;-1).Даны три вектора: 1)
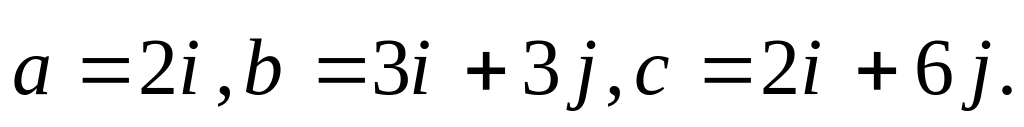 2)
2)
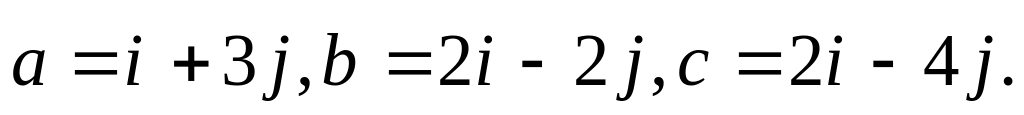 Разложить
вектор
по
векторам
и
.
Разложить
вектор
по
векторам
и
.Даны векторы и . Доказать, что они образуют базис. Найти координаты вектора в этом базисе, если 1)
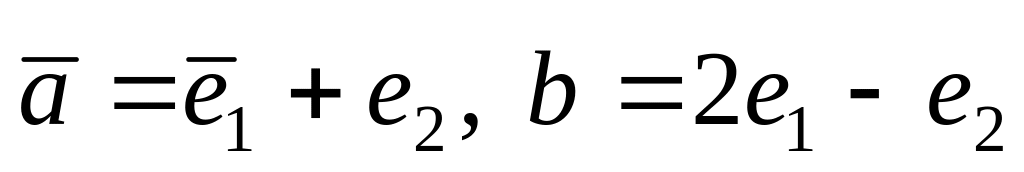 ,
где
,
где
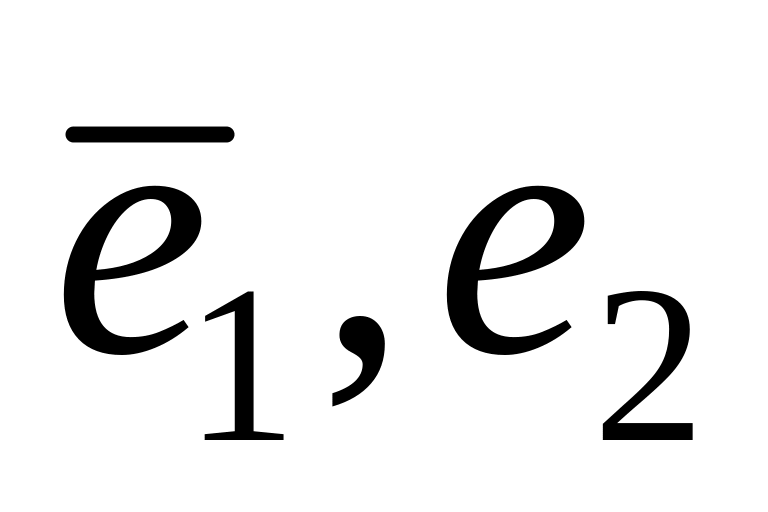 -
базис,
-
базис,
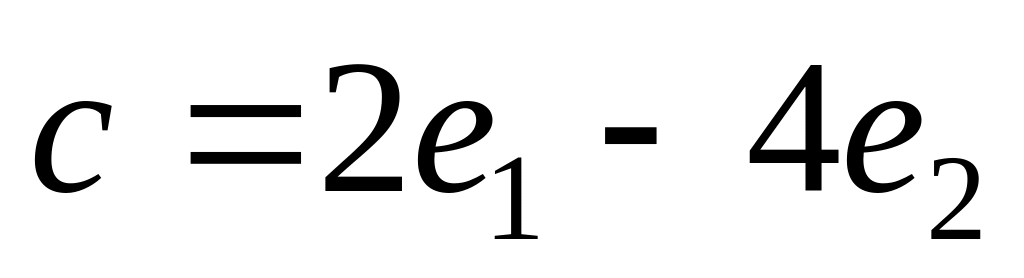 ,
2)
,
2)
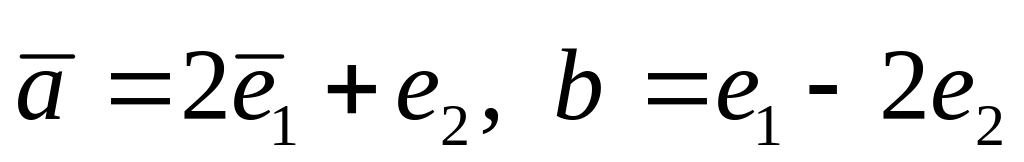 ,
где
-
базис,
,
где
-
базис,
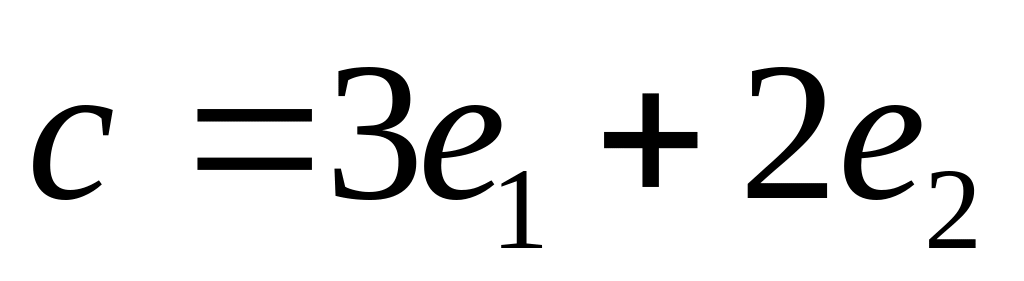 .
.Проверить наличие линейной зависимости системы векторов в пространстве R2.
-
1).
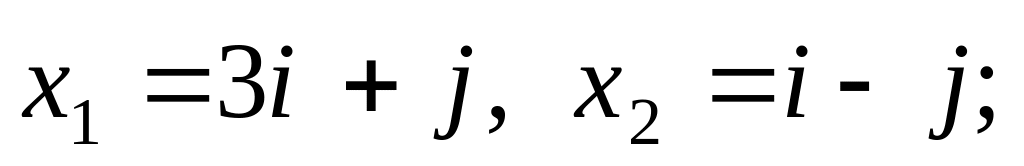
2).
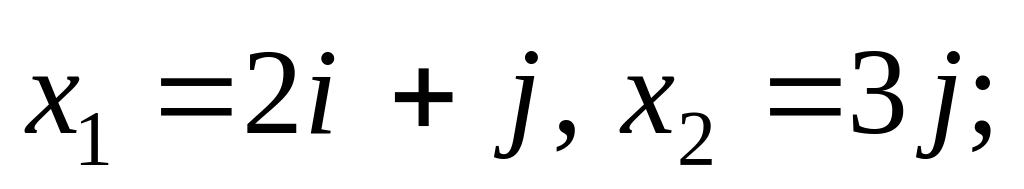
3).
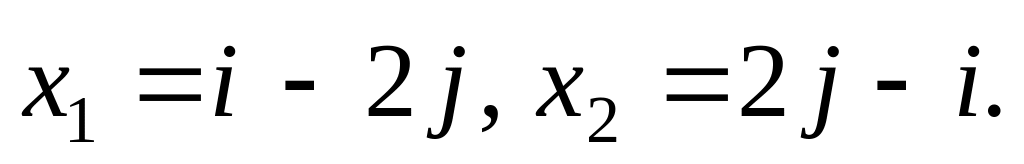
50. Определить ранг следующих матриц:
51. Какие из указанных векторов являются собственными векторами матрицы А?
-
а)
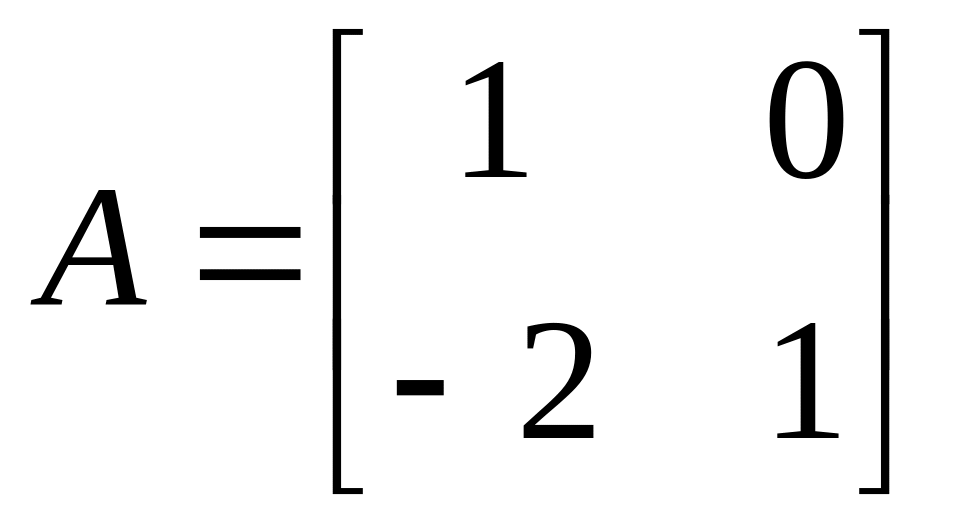
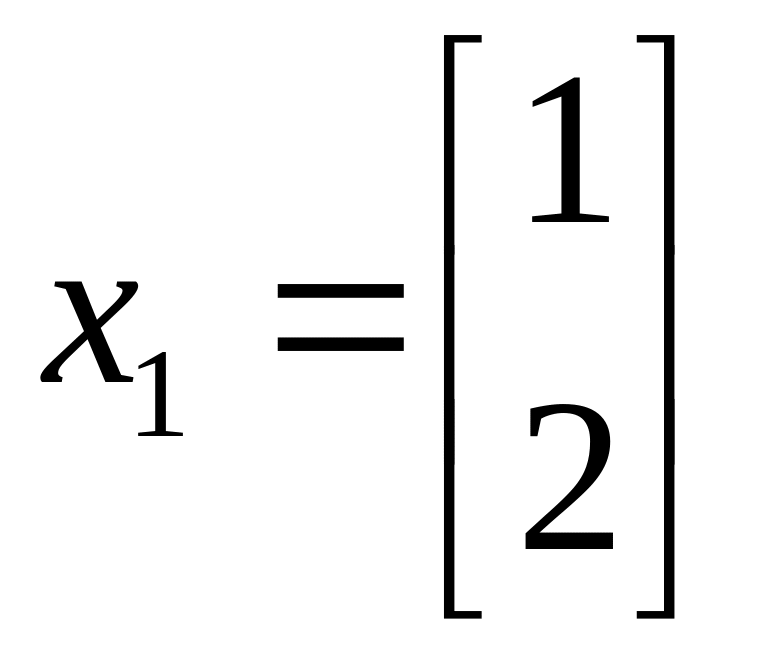
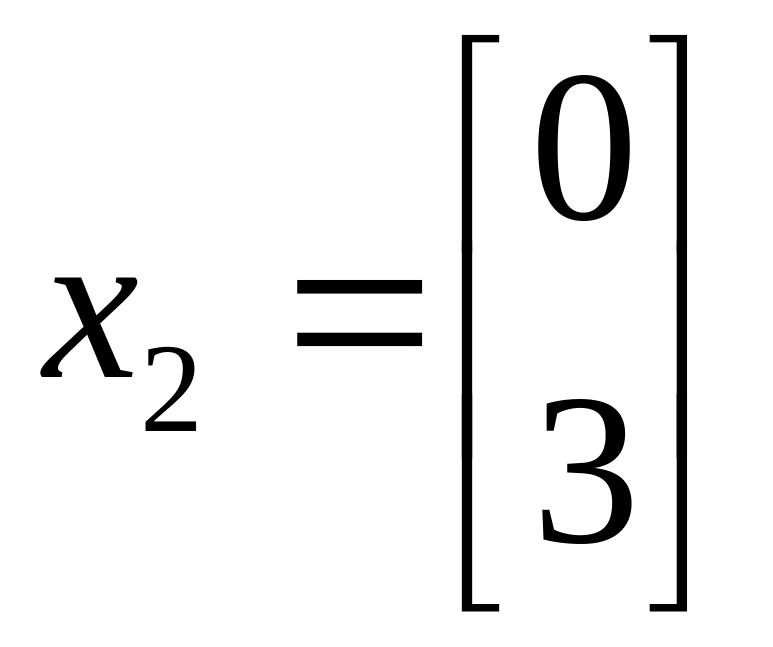
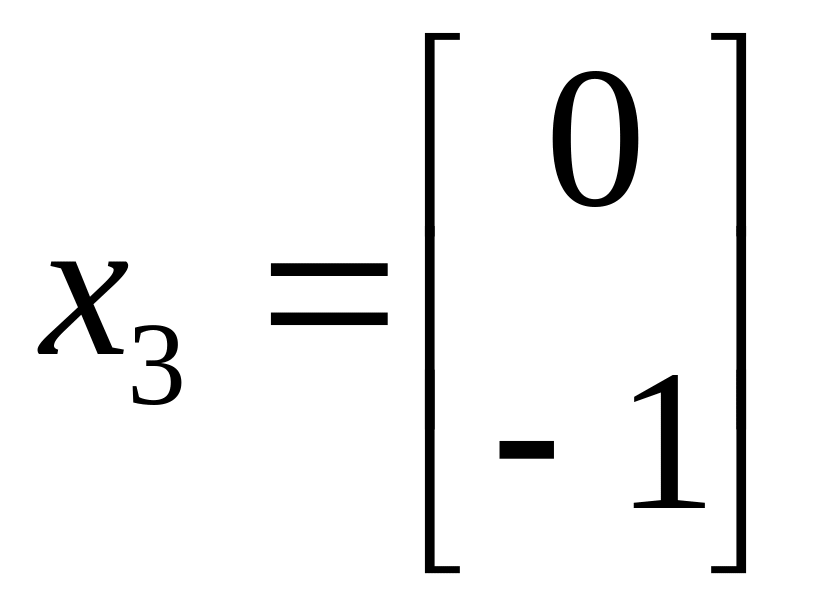
б)
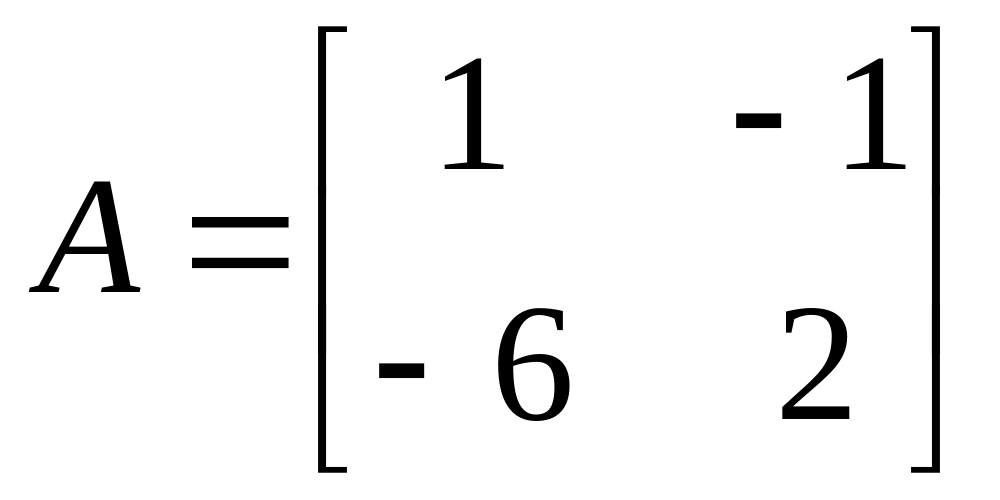
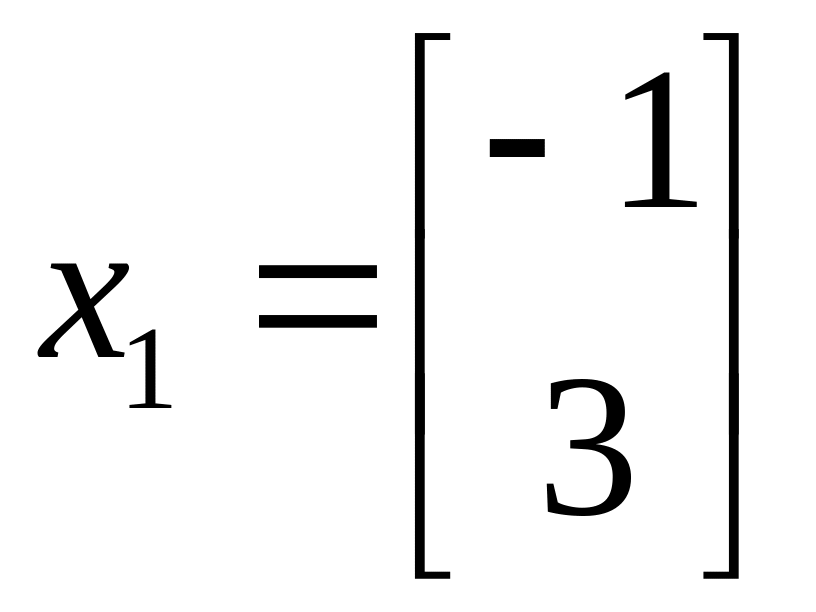
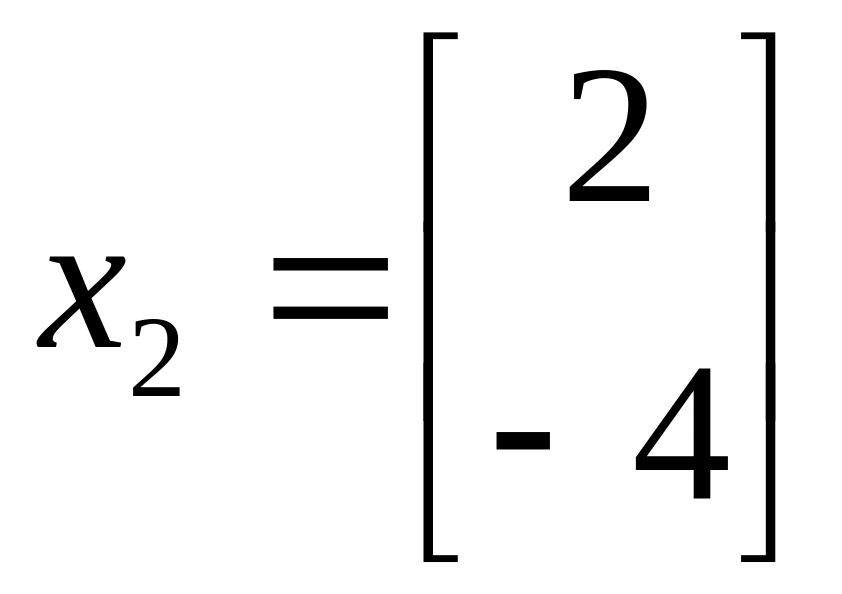
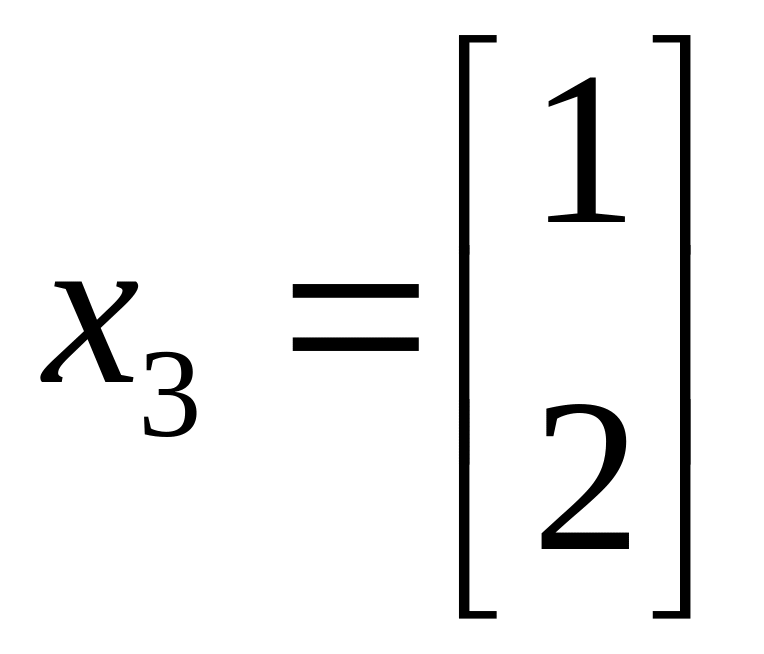
в)