МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ, СТАТИСТИКИ И ИНФОРМАТИКИ
Семестровая работа по курсу
«Диагностика кризисного состояния предприятия»
Выполнила:
Шкляева Виктория Викторовна
Группа: ДЭС-401
Проверил:
д.т.н., профессор
Фомин Ярослав Алексеевич
Москва, 2011
Введение.
В данной работе будет производиться анализ Австралии, а также стран Восточной и Западной Европы, которые предварительно разделены на 2 группы: передовые страны и отстающие. За основу дискриминации взяты несколько основных показателей социально-экономического развития страны. Для первоначального разбиения использовался показатель «Ожидаемая продолжительность жизни»
Кроме того, проводится сравнение уровня развития России и других стран в динамике за 2007-2010 годы.
Исходные данные.
Признак |
|
|||
Передовые страны S1 |
||||
X1(1) |
X2(1) |
X3(1) |
X4(1) |
|
Ожидаемая продолжительность жизни |
76,9 |
78,1 |
76,8 |
75,8 |
ВВП на душу населения |
29,53 |
37,3 |
29,29 |
33,74 |
Занятость, млн |
19,39 |
10,76 |
23,00 |
25,38 |
X1(1) – Испания
X2(1) – Австралия
X3(1) – Италия
X4(1) – Франция
Признак |
Отстающие страны S2 |
|||
X1(1) |
X2(1) |
X3(1) |
X4(1) |
|
Ожидаемая продолжительность жизни |
62,71 |
62,6 |
58,8 |
64,5 |
ВВП на душу населения |
12,48 |
64,6 |
15,04 |
27,66 |
Занятость, млн |
9,356 |
7,567 |
16,346 |
5,164 |
X1(1) – Беларусь
X2(1) – Украина
X3(1) – Россия
X4(1) – Молдавия
Обучение с тремя показателями.
Для групп стран S1 и S2 составим векторы средних (соответственно а1 и а2), а также их разность.
|
76,90 |
|
62,15 |
|
14,75 |
|
139,05 |
а1= |
32,47 |
а2= |
29,95 |
а1+а2= |
2,52 |
а1-а2= |
62,41 |
|
19,63 |
|
9,61 |
|
10,02 |
|
29,24 |
Вычислим ковариационные матрицы М1 и М2, где m1 и m2 количество передовых и отсталых стран
Ковариационная матрица М1
|
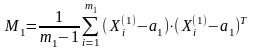
0,00 |
|
|
|
|
|
(X1(1)-a1)= |
-2,94 |
|
(X1(1)-a1)T= |
0,00 |
-2,94 |
-0,24 |
|
-0,24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1,20 |
|
|
|
|
|
(X2(1)-a1)= |
4,83 |
|
(X2(1)-a1)T= |
1,2 |
4,835 |
-8,873 |
|
-8,87 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,10 |
|
|
|
|
|
(X3(1)-a1)= |
-3,18 |
|
(X3(1)-a1)T= |
-0,1 |
-3,175 |
3,363 |
|
3,36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-1,10 |
|
|
|
|
|
(X4(1)-a1)= |
1,28 |
|
(X4(1)-a1)T= |
-1,1 |
1,275 |
5,752 |
|
5,75 |
|
|
|
|
|
|
0 |
0 |
0 |
|
|
(X1(1)-a1)(X1(1)-a1)T = |
0 |
8,614225 |
0,71027 |
|
|
|
0 |
0,71027 |
0,058564 |
|
|
|
|
|
|
|
|
|
1,44 |
5,802 |
-10,6476 |
|
|
(X2(1)-a1)(X2(1)-a1)T = |
5,802 |
23,377225 |
-42,900955 |
|
|
|
-10,6476 |
-42,900955 |
78,730129 |
|
|
|
|
|
|
|
|
|
0,01 |
0,3175 |
-0,3363 |
|
|
(X3(1)-a1)(X3(1)-a1)T = |
0,3175 |
10,080625 |
-10,677525 |
|
|
|
-0,3363 |
-10,677525 |
11,309769 |
|
|
|
|
|
|
|
|
|
1,21 |
-1,4025 |
-6,3272 |
|
|
(X4(1)-a1)(X4(1)-a1)T = |
-1,4025 |
1,625625 |
7,3338 |
|
|
|
-6,3272 |
7,3338 |
33,085504 |
|
|
|
|
|
|
|
|
|
2,66 |
4,717 |
-17,3111 |
|
|
Сумма = |
4,717 |
43,6977 |
-45,53441 |
|
|
|
-17,3111 |
-45,53441 |
123,183966 |
|
|
|
|
|
|
|
|
|
0,886666667 |
1,572333333 |
-5,770366667 |
||
М1 = |
1,572333333 |
14,5659 |
-15,17813667 |
||
|
-5,770366667 |
-15,17813667 |
41,061322 |
||
Ковариационная матрица М2
|
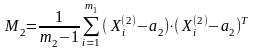
0,56 |
|
|
|
|
|
(X1(2)-a2)= |
-17,47 |
|
(X1(2)-a2)T= |
0,56 |
-17,47 |
-0,25 |
|
-0,25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,45 |
|
|
|
|
|
(X2(2)-a2)= |
34,66 |
|
(X2(2)-a2)T= |
0,45 |
34,66 |
-2,04 |
|
-2,04 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-3,35 |
|
|
|
|
|
(X3(2)-a2)= |
-14,91 |
|
(X3(2)-a2)T= |
-3,35 |
-14,91 |
6,74 |
|
6,74 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2,35 |
|
|
|
|
|
(X4(2)-a2)= |
-2,29 |
|
(X4(2)-a2)T= |
2,35 |
-2,29 |
-4,44 |
|
-4,44 |
|
|
|
|
|
|
0,31 |
-9,74 |
-0,14 |
(X1(2)-a2)(X1(2)-a2)T = |
-9,74 |
305,03 |
4,41 |
|
-0,14 |
4,41 |
0,06 |
|
|
|
|
|
0,20 |
15,51 |
-0,91 |
(X2(2)-a2)(X2(2)-a2)T = |
15,51 |
1200,97 |
-70,74 |
|
-0,91 |
-70,74 |
4,17 |
|
|
|
|
|
11,24 |
49,97 |
-22,59 |
(X3(2)-a2)(X3(1)-a2)T = |
49,97 |
222,16 |
-100,43 |
|
-22,59 |
-100,43 |
45,40 |
|
|
|
|
|
5,51 |
-5,36 |
-10,43 |
(X4(2)-a2)(X4(2)-a2)T = |
-5,3640375 |
5,221225 |
10,15511 |
|
-10,432877 |
10,15511 |
19,75136 |
|
|
|
|
|
17,26 |
50,38 |
-34,08 |
Сумма = |
50,38 |
1733,38 |
-156,61 |
|
-34,08 |
-156,61 |
69,38 |
|
|
|
|
|
5,75369167 |
16,79212 |
-11,35842 |
М2 = |
16,7921167 |
577,7918 |
-52,20168 |
|
-11,358424 |
-52,20168 |
23,12632 |
Найдём общую ковариационную матрицу М
|
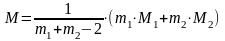
4,426905556 |
12,24296667 |
-11,41919389 |
М = |
12,24296667 |
394,9051556 |
-44,91987444 |
|
-11,41919389 |
-44,91987444 |
42,79176239 |
Найдём обратную матрицу М-1
|
0,7249272348 |
-0,0005334017 |
0,1928904970 |
M-1 = |
-0,0005334017 |
0,0028760105 |
0,0028766988 |
|
0,1928904970 |
0,0028766988 |
0,0778625312 |
Найдём произведение транспонированной разности векторов средних групп стран (а1-а2)Т и обратной общей ковариационной матрицы M-1
(а1-а2)T = |
14,7475 |
2,52 |
10,02375 |
|
|
|
|
1/2*(а1-а2)T = |
7,37375 |
1,26 |
5,011875 |
|
|
|
|
(а1-а2)T M-1 = |
12,62300634 |
0,028216515 |
3,632376433 |
|
|
|
|
1/2 (а1-а2)T M-1 = |
6,311503171 |
0,014108258 |
1,816188216 |
Для определения достоверности:
Вычислим расстояние Махаланобиса:
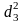=222,638
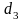=14,92
Найдем
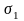и
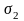
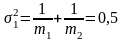
0,707
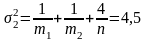
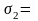2,121
Найдем
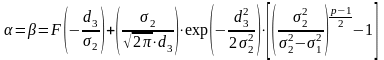
p=3
=0,00441
=
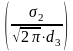0,0567
=
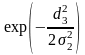0,00
=
1,125
=0,0132
Достоверность
прогноза равна
=
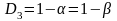0,9868