1. Представление конструктивной объемной геометрии (constructive solid geometry

(CSG)). CSG представление сохраняет в некотором графе хронологию применения булевых операций на примитивах. Этот граф называют CSG деревом. CSG представление сохраняет последовательность применения булевых операций на примитивах.

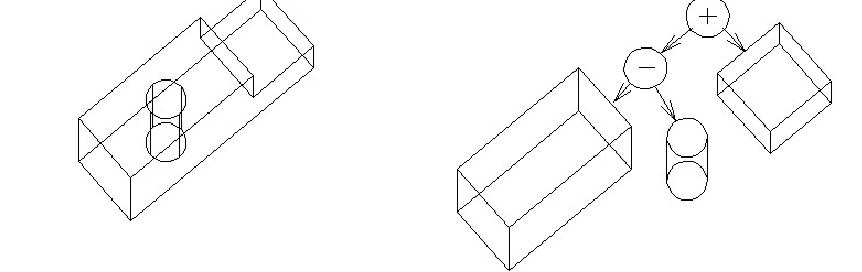
CSG представление имеет следующие преимущества:

- Структура данных проста и компактна. Соответственно, управление данными будет простым.

- Тело, сохраненное в CSG дереве будет всегда правильным телом.

- CSG представление тела может всегда преобразовано в соответствующее B-rep представление. Таким образом, CSG представление может быть связано соответствующим интерфейсом с прикладными программами, написанными для B-Rep.

- Параметрическое моделирование может быть легко реализовано путем изменения параметров соответствующих примитивов.

Недостатки:

- Поскольку CSG древовидная структура сохраняет последовательность применения булевых операций, то только эти операции разрешены в процессе моделирования, поэтому диапазон форм, которые будут смоделированы, строго ограничен. Кроме того, функции модификации типа сопряжения нельзя использовать.

- Требуется выполнить большой объем вычислений, чтобы из CSG дерева получить

информацию относительно граней, ребер и вершин и обеспечения связи между этими граничными объектами.

2. Граничное представление (boundary representation (B-Rep )) сохраняет граничную информацию для тела (вершины, ребра и грани вместе с информацией относительно того, как они связаны между собой). Эту структуру данных называют B-Rep структурой данных. Последовательность ребер для каждой грани определяется против часовой стрелки, когда тело рассматривается с его внешней стороны. Это правило позволяет иметь информацию о том, где находится внутренняя и внешняя часть тела, т.е. можно для любой точки определить, расположена ли она на внутренней или внешней части тела.

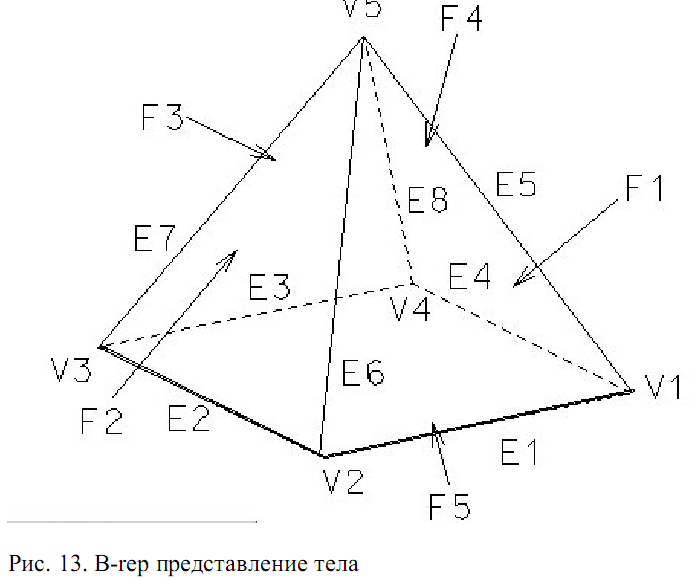
3. Декомпозиционная модель (decomposition model) сохраняет тело как агрегат из простых тел типа параллелепипедов. Можно выделить три типа таких моделей:

- Вокселные модели;

- Модели в форме дерева октантов (octree);

- Ячеечные модели.

Вокселная модель – это трехмерное расширение растрового представления двумерных форм (воксел - трехмерный аналог пиксела: pixel - picture element, voxel - volume element).

Напомним основы растрового моделирования. Сначала создается квадрат области моделирования. Затем эта область разделяется на много маленьких квадратов линиями координатной сетки. Выбор интервалов между линиями координатной сетки зависит от желаемой точности растрового представления. Квадрат области моделирования, содержащий много маленьких квадратов, представляется в компьютере двумерным массивом. Элементы массива, соответствующие маленьким квадратам, перекрывающим моделируемые объекты, имеют значение 1, а остающиеся элементы имеют значение 0. Таким образом, массив из 1 и 0 является растровым представлением двумерного объекта.

Представление трехмерного тела основано на такой же процедуре, как и растровое представление. Большой куб области моделирования разделяется на маленькие кубы, называемые вокселами, с помощью объемной сетки с равным шагом по осям x, y и z. Этот куб представляется в компьютере трехмерным массивом, каждый элемент которого имеет значение 1 или 0, в зависимости от позиции воксела в моделируемом теле. Хотя процесс получения вокселной модели почти такой же, как процесс растеризации, обнаружение перекрытия между телом и вокселом требует более сложных вычислений, чем вычисления в процессе растеризации.

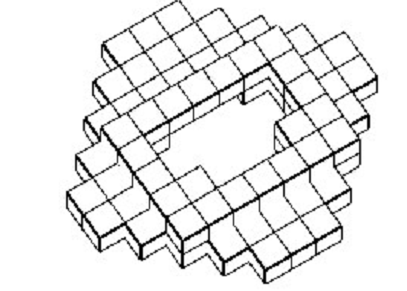
Вокселные модели имеют следующие преимущества:

- Тело произвольной формы может всегда можно описать достаточно точно. Например, модели человеческих костей в томографии обычно представляются вокселными моделями.

- Легко вычислять массо-инерционные параметры тел простым суммированием соответствующих параметров вокселов.

- На таких моделях очень просто выполнять булевы операции.

- Легко моделировать препятствия при движении роботов.

Однако вокселные модели имеют и недостатки: - Требования к затратам памяти резко увеличивается при повышении точности моделирования. - Вокселные модели принципиально являются только приближенными.

Модели в форме дерева октантов представляют тело как множество кубов, но при этом требования к затратам памяти меньше, так как область моделирования делится на кубы по другому, чем для вокселных моделей. В вокселных моделях область моделирования разделяется на одинаковые по размерам кубы, независимо от представляемого тела. В моделях в форме дерева октантов, исходный куб области моделирования разделяется на восемь одинаковых кубов, которые в дальнейшем также делятся на восемь одинаковых кубов, соответственно, как показано на рис. 15.

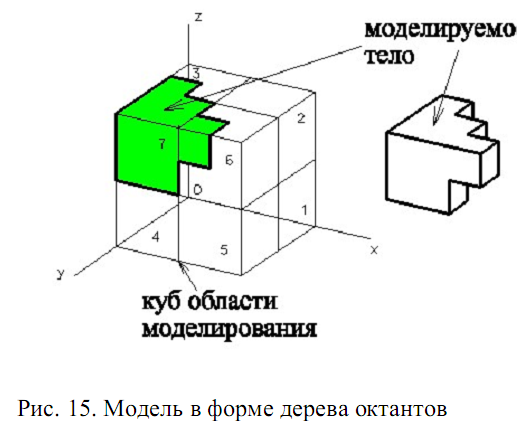
Рис. 15. Модель в форме дерева октантов

Таким образом, каждый куб - это одна восьмая по размерам от его родительского куба и поэтому он называется октантом. В свою очередь все октанты могут быть представлены как узлы дерева, в котором каждый узел имеет восемь ветвей.

Процедура получения модели в форме октантов следующая. Сначала создается исходный куб области моделирования, который полностью содержит тело, которое будет моделироваться. Этот куб называется корневым октантом. Затем корневой октант разделяется на восемь октантов и рассматривается взаимное пространственное отношение каждого октанта относительно моделируемого тела. Если октант расположен полностью в теле, то он отмечается как "черный" (рис. 16.). Если он расположен полностью вне тела, он отмечается как "белый" (рис. 16.). Если он расположен частично внутри и частично снаружи тела, то он отмечается как "серый" (рис. 16.) и только такой октант разделяется в дальнейшем на восемь дочерних октантов. Октанты, отмеченные как черные или белые, далее не разделяются.

Этот шаг рекурсивно повторяется до тех пор, пока не останется более серых октантов. Множество черных октантов в полученном дереве и будут моделировать тело. Рис. 16. иллюстрирует дерево октантов, сгенерированное для тела, показанного на рис. 15. Число октантов, которые будут храниться в памяти, намного меньше, чем число вокселов в вокселных моделях, т.к. октанты отмеченные как черные или белые не участвуют далее в разделениях.

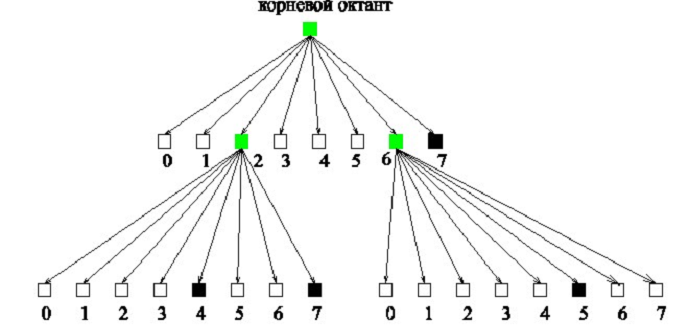
Рис. 16. Дерево октантов

Ячеечные модели представляют тело как множество простых ячеек, как и в вокселных моделях. Однако в этих моделях не накладывается строгое ограничение на допустимую форму ячеек, которые используются. В результате любое тело может быть представлено только небольшим количеством простых ячеек. Разделение тела на множество конечных элементов при анализе тел на прочность является типичным примером ячеечного моделирования.

К методам компьютерной графики относят методы преобразования графических объектов, представления (развертки) линий в растровой форме, выделения окна, удаления скрытых линий, проецирования, закраски изображений.

Перенос точки из положения   в новое положение   можно выполнять по формулам типа где   — приращение по координате  . Однако удобнее операции преобразования представлять в единой матричной форме

(1)

где   — преобразующая матрица. Выражение для сдвига с одновременным поворотом имеет вид где  ,   — матрица сдвига,   — матрица поворота.

Представление графических элементов в растровой форме требуется для отображения этих элементов на битовую карту растровой видеосистемы. Растр - точечная (в виде совокупности точек) структура графического изображения при полиграфической и цифровой печати. 

Цель процесса растрирования ≈ сделать этот процесс невидимым. Правильно выполненное цифровое растрирование создает иллюзию непрерывного тона. Это достигается с помощью амплитудного (AM =полутонового) растрирования,  в рамках которого точки переменного размера размещаются в регулярной матрице. Области изображения, составленные из больших точек, воспринимаются как более темные тона, а из небольших точек ≈ как более светлые.

Растровая форма описывается тремя параметрами: пространственной частотой (плотность растра), формой точки и углом поворота. Каждый из этих факторов по-своему влияет на качество отпечатанного изображения.

Пусть требуется развернуть отрезок   прямой  , причем   (при других значениях   рассматриваемый ниже алгоритм остается справедливым после определенных модификаций). Введем обозначения:     за величину дискрета (пиксела) примем единицу. В алгоритме развертки номера строк и столбцов карты, на пересечении которых должны находиться точки отрезка, определяются следующим образом:

если  , то   иначе 

переход к пункту 3, пока не достигнута точка  . Экономичность этого алгоритма обусловливается отсутствием длинных арифметических операций типа умножения.

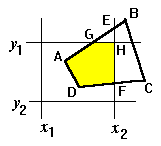
Выделение окна требуется при определении той части сцены, которая должна быть выведена на экран дисплея.

Применяют ряд алгоритмов удаления скрытых линий. Один из наиболее просто реализуемых алгоритмов — алгоритм z-буфера, где z-буфер — область памяти, число ячеек в которой равно числу пикселов в окне вывода. Предполагается, что ось   направлена по нормали к видовой поверхности и наблюдатель расположен в точке  .

В начале исполнения алгоритма все пикселы соответствуют максимальному значению  , т.е. максимальному удалению от наблюдателя, что приводит к помещению во все ячейки z-буфера значений пикселов фона картины (чертежа). Далее поочередно для всех точек граней рассчитываются значения координаты  . Среди точек, относящихся к одному и тому же пикселу (одной и той же ячейке z-буфера  ), выбирается точка с наименьшим значением  и ее код (т.е. цвет и яркость) помещается в  . В итоге z-буфер будет содержать пикселы наиболее близких к наблюдателю граней.

Моделирование эффектов отражения света от поверхности объекта в геометрических моделях называют рендерингом. Закраска матовых поверхностей основана на законе Ламберта, согласно которому яркость отраженного от поверхности света пропорциональна  , где   — угол между нормалью к поверхности и направлением луча падающего света. В алгоритме Гуро яркость внутренних точек рассматриваемой поверхности определяется линейной интерполяцией яркости в вершинах многоугольника. При этом сначала проводится интерполяция в точках ребер, а затем по строкам горизонтальной развертки. Более реалистичными получаются изображения в алгоритме Фонга, основанном на линейной интерполяции векторов нормалей к поверхности.

Важной составной частью геометрических моделей является описание поверхностей. Если поверхности детали — плоские грани, то модель может быть выражена достаточно просто определенной информацией о гранях, ребрах, вершинах детали методом конструктивной геометрии или полигональными сетками, если эти поверхности можно аппроксимировать множествами плоских участков. Аппроксимация полигональными сетками при больших размерах ячеек сетки дает заметные искажения формы, а при малых размерах ячеек оказывается неэффективной по вычислительным затратам.

Поэтому более популярны описания неплоских поверхностей кубическими уравнениями в форме Безье или B-сплайнов. Знакомство с этими формами удобно выполнить, показав их применение для описания геометрических объектов первого уровня — пространственных кривых.

В подсистемах графики и геометрического моделирования используются параметрически задаваемые кубические кривые

(1)

где  .

Применение кубических кривых обеспечивает (соответствующим выбором четырех коэффициентов в каждом из трех уравнений) выполнение четырех условий сопряжения сегментов. В случае модели Безье этими условиями являются прохождение кривой сегмента через две заданные концевые точки и равенство в этих точках касательных векторов соседних сегментов. В случае B-сплайнов выполняются условия непрерывности касательного вектора и кривизны (т.е. первой и второй производных) в концевых точках сегментов. Использование сплайнов обеспечивает высокую степень "гладкости" кривой, хотя прохождение аппроксимирующей кривой через заданные точки здесь не обеспечивается. Применение полиномов выше третьей степени не рекомендуется, так как велика вероятность появления "волнистости".

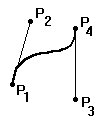рис. кривая Безье