Тема: Электростатическое поле в вакууме
1.Сила взаимодействия двух отрицательных точечных зарядов, находящихся на расстоянии R друг от друга, равна F. Знаки зарядов обеих частиц изменили на противоположные. Чтобы сила взаимодействия F не изменилась, расстояние между зарядами надо …
уменьшить в 2 раза
оставить без изменения
увеличить в 4 раза
уменьшить в
![]()
увеличить в 2 раза
Решение:
![]() - Оставить без изменения
- Оставить без изменения
2. На рисунке показано направление
вектора
![]() напряженности
результирующего электрического поля
точечных зарядов q1 и q2 в
точке А.
напряженности
результирующего электрического поля
точечных зарядов q1 и q2 в
точке А.
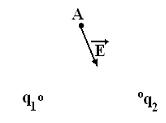 При
этом для зарядов
При
этом для зарядов
![]() и
и
![]() справедливо
соотношение…
справедливо
соотношение…
![]() ,
,
![]() ;
,
;
,
![]() ;
;
![]() ,
;
,
,
;
,
Решение: Построить все варианты. , - да.
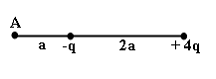
3. Электростатическое поле создано
двумя точечными зарядами:
![]() и
и
![]() .
Отношение потенциала поля, созданного
вторым зарядом в точке А, к потенциалу
результирующего поля в этой точке
равно … 4
.
Отношение потенциала поля, созданного
вторым зарядом в точке А, к потенциалу
результирующего поля в этой точке
равно … 4
Решение:
 (Коэффициенты
(Коэффициенты
![]() при делении сокращаются)
при делении сокращаются)
4. Электростатическое поле создано
системой точечных зарядов.
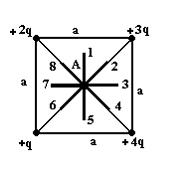
Вектор напряженности
![]() поля
в точке А ориентирован в направлении …7
поля
в точке А ориентирован в направлении …7
Решение:
Согласно принципу суперпозиции полей
напряженность в точке А равна:
![]() ,
где
,
где
![]() –
векторы напряженности полей, создаваемых
точечными зарядами Сделать рисунок.
–
векторы напряженности полей, создаваемых
точечными зарядами Сделать рисунок.
5. Электростатическое поле создано
системой точечных зарядов
,
![]() и
.
и
.
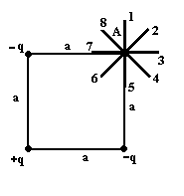 Градиент
потенциала поля в точке А ориентирован
в направлении …2
Градиент
потенциала поля в точке А ориентирован
в направлении …2
Решение:
Диагональ равна
![]() .
Напряженность от зарядов
.
Напряженность от зарядов
![]() направлена в т. А по 6 и равна по величине
направлена в т. А по 6 и равна по величине
 .
Напряженность от заряда
.
Напряженность от заряда
![]() в т.А направлена по 2 и по величине равна
в т.А направлена по 2 и по величине равна
 .
Так как
.
Так как
 ,
то напряженность в т.А направлена по 6.
Следовательно
,
то напряженность в т.А направлена по 6.
Следовательно
![]() по 2. ( для простоты опущены коэф.-ты
)
по 2. ( для простоты опущены коэф.-ты
)
6.Вектор напряженности электростатического
поля в точке А между эквипотенциальными
поверхностями
![]() В
и
В
и
![]() В
имеет направление …
В
имеет направление …

в, а, б, г
Решение:
Т.к. вектор![]() ,
то вектор
,
то вектор
![]() всегда направлен в сторону уменьшения
всегда направлен в сторону уменьшения
![]() перпендикулярно эквипотенциальным
поверхностям, т.е. по направлению г.
перпендикулярно эквипотенциальным
поверхностям, т.е. по направлению г.
7. Электростатическое поле создано
системой точечных зарядов.
 Вектор
напряженности
Вектор
напряженности
![]() поля
в точке А ориентирован в направлении …6
поля
в точке А ориентирован в направлении …6
Решение:
Согласно принципу
суперпозиции полей напряженность в
точке А равна:
,
где
–
векторы напряженности полей, создаваемых
точечными зарядами
![]() ,
,
,
,
![]() ,
,
![]() в
рассматриваемой точке соответственно.
На рисунке показаны направления этих
векторов.
в
рассматриваемой точке соответственно.
На рисунке показаны направления этих
векторов.
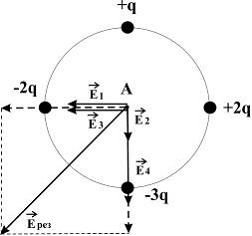
 .
Учитывая величины зарядов и то, что
точка А одинаково удалена от каждого
заряда, можно сделать вывод, что
.
Учитывая величины зарядов и то, что
точка А одинаково удалена от каждого
заряда, можно сделать вывод, что
![]() образует
диагональ квадрата со стороной 2Е1.
Таким образом, вектор напряженности
поля
в точке А ориентирован в направлении
6.
образует
диагональ квадрата со стороной 2Е1.
Таким образом, вектор напряженности
поля
в точке А ориентирован в направлении
6.
8. В некоторой
области пространства создано
электростатическое поле, потенциал
которого описывается функцией
![]() .
Вектор напряженности электрического
поля в точке пространства, показанной
на рисунке, будет иметь направление
…
Р
.
Вектор напряженности электрического
поля в точке пространства, показанной
на рисунке, будет иметь направление
…
Р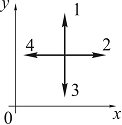 ешение:
ешение:
![]() ,
,
![]() ,
,
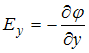 ,
,
![]() .
Следовательно
.
Следовательно
![]() ,
т.е. вектор напряженности направлен
по 4.
,
т.е. вектор напряженности направлен
по 4.
9. Электростатическое
поле образовано двумя параллельными
бесконечными плоскостями, заряженными
разноименными зарядами с одинаковой
по величине поверхностной плотностью
заряда. Расстояние между плоскостями
равно d.
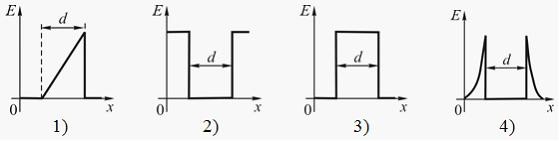 Распределение
напряженности Е
такого поля вдоль оси х,
перпендикулярной
плоскостям, правильно показано на
рисунке …
Распределение
напряженности Е
такого поля вдоль оси х,
перпендикулярной
плоскостям, правильно показано на
рисунке …
Решение:
Электростатическое
поле, в этом случае, сосредоточено между
плоскостями и является однородным.
Напряженность поля постоянна и не
зависит от х, а вне – равна нулю. Таким
образом, правильный график
![]() на рисунке 3.
на рисунке 3.
10.  Электрическое
поле создано двумя параллельными
плоскостями, заряженными с поверхностными
плотностями –2σ
и +σ. На рис. 3.1 показана качественная
зависимость проекции напряженности Ех
от координаты х
вне пластин и между пластинами. Правильно
отражает характер изменения потенциала
φ этого поля график
Электрическое
поле создано двумя параллельными
плоскостями, заряженными с поверхностными
плотностями –2σ
и +σ. На рис. 3.1 показана качественная
зависимость проекции напряженности Ех
от координаты х
вне пластин и между пластинами. Правильно
отражает характер изменения потенциала
φ этого поля график
1) на рис. 3.2 |
2) на рис. 3.3 |
3) на рис. 3.4 |
4) на рис. 3.5 |
φ
Рис. 3.2 |
φ
Рис. 3.3 |
Р
φ
φ |
Р
φ |
Решение:
Знак
![]() позволяет определить направление
.
Т.к. вдоль направления в-ра
ф-ция
убывает, то правильный Рис. 3.4
позволяет определить направление
.
Т.к. вдоль направления в-ра
ф-ция
убывает, то правильный Рис. 3.4
11. Электрическое поле создано двумя параллельными плоскостями, заряженными с поверхностными плотностями +σ и –2σ. Качественная зависимость потенциала поля φ от координаты х вне пластин и между пластинами правильно показана на графике
1) рис. 3.6 |
2) рис. 3.7 |
3) рис. 3.8 |
4) рис. 3.9 |
+σ
–2σ
φ
0 Рис. 3.6 |
+σ
–2σ
φ
0 Рис. 3.7 |
φ
0
–2σ
+σ Рис. 3.8 |
0
φ
–2σ
+σ Рис. 3.9 |
Решение:
Определяем направление в-ра во всех (3х) областях пространства. Т.к. вдоль направления в-ра ф-ция убывает, то правильный Рис. 3.6. ( более просто - для этой системы меняется)
12. Эквипотенциальные линии системы зарядов и значения потенциалов на них показаны на рис. 3.10. Вектор напряженности электрического поля в точке А ориентирован в направлении
1) 1 |
2) 2 |
3) 3 |
4) 4 |

Решение:
Т.к. вдоль направления в-ра ф-ция убывает, то правильное напр. 3
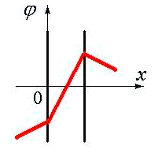
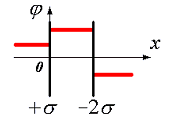
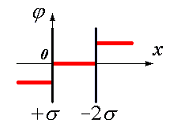
13. Электрическое поле создано двумя параллельными плоскостями, заряженными с поверхностными плотностями –2σ и +σ. На рис. 3.11 дана зависимость изменения потенциала φ этого поля от координаты х вне пластин и между пластинами. Правильно отражает качественную зависимость проекции напряженности поля Ех на ось х график
1) на рис. 3.12 |
2) на рис. 3.13 |
3) на рис. 3.14 |
4) на рис. 3.15 |
Р |
Р |
Р |
Р |
Решение:
Т.к. вдоль направления в-ра ф-ция убывает, то определяем направление и знак проекции в-ра на ось ОХ. Правильный рис.3.13
14. Система точечных зарядов в вакууме и замкнутые поверхности S1, S2 и S3 даны на рис. 3.16. Поток вектора напряженности электрического поля равен нулю через поверхности
1) S1 |
2) S2 |
3) S3 |

Решение:
Поток через произв.замкнутую поверхность равен нулю, если внутри поверхности суммарный заряд равен нулю, т.е. S2, S3.
15.Система точечных зарядов в вакууме и замкнутые поверхности S1, S2 и S3 даны на рис. 3.17. Поток вектора напряженности электрического поля отличен от нуля через поверхности
1) S1 |
2) S2 |
3) S3 |
Решение:
Поток через произв.замкнутую поверхность не равен нулю, если внутри поверхности суммарный заряд не равен нулю, т.е. S1, S2.
16. Точечный заряд + q находится в центре сферической поверхности. Если уменьшить радиус сферической поверхности, то поток вектора напряженности электрического поля через поверхность сферы
1) уменьшится |
2) увеличится |
3) не изменится |
Решение:
Поток через замкнутую поверхность зависит только от суммарного заряда внутри. Ответ - не изменится
17. Точечный заряд + q находится в центре сферической поверхности. Если заряд сместить из центра сферы, оставляя его внутри нее, то поток вектора напряженности электрического поля через поверхность сферы
1) уменьшится |
2) увеличится |
3) не изменится |
Решение:
Поток через замкнутую поверхность зависит только от суммарного заряда внутри. Ответ - не изменится
18. Точечный заряд + q находится в центре сферической поверхности. Если добавить заряд – q внутрь сферы, то поток вектора напряженности электрического поля через поверхность сферы
1) уменьшится |
2) увеличится |
3) не изменится |
Решение:
Поток через замкнутую поверхность зависит только от заряда внутри, а он стал нулевым, т.е. уменьшится( был положительным).
19. Относительно статических электрических полей справедливо утверждение:
1) электростатическое поле действует как на электрические, так и на магнитные заряды |
2) электростатическое поле является потенциальным |
3) поток вектора напряженности электростатического поля сквозь произвольную замкнутую поверхность всегда равен нулю |
Решение: 1 и 3 – не верны, 2 – верно.
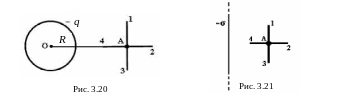
20. Поле создано равномерно заряженной сферической поверхностью с зарядом – q (рис. 3.20). Укажите направление вектора градиента потенциала в точке А.
1) 1 |
2) 2 |
3) 3 |
4) 4 |
Решение:
Направление в-ра градиента потенциала – обратное в-ру . Так как заряд отрицательный, то в-р в т.А направлен по 4.Следовательно градиент – по 2.
21. Поле создано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда – σ (рис. 3.21). Укажите направление вектора градиента потенциала в точке А.
1) 1 |
2) 2 |
3) 3 |
4) 4 |
Решение:
Направление в-ра градиента потенциала – обратное в-ру . Так как заряд отрицательный, то в-р в т.А направлен по 4.Следовательно градиент – по 2.
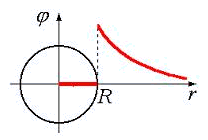
22. Зависимость потенциала электрического поля φ от расстояния r между центром равномерно заряженной проводящей сферы радиусом R и точкой, где определяется потенциал, правильно изображена на графике
1) рис. 3.22 |
2) рис. 3.23 |
3) рис. 3.24 |
4) рис. 3.25 |
Р
φ |
Р
φ |
Р
φ |
Р
φ |
Решение: рис. 3.25
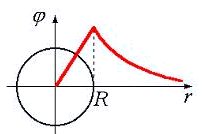
23. Зависимость потенциала электрического поля φ от расстояния r между центром равномерно заряженного проводящего сплошного шара радиусом R и точкой, где определяется потенциал, правильно изображена на графике
1) рис. 3.22 |
2) рис. 3.23 |
3) рис. 3.24 |
4) рис. 3.25 |
Решение: рис. 3.25 Между проводящей сферой и сплошным проводящим шаром нет разницы. Но что такое равномерно заряженный шар? По поверхности?






 ис.
3.12
ис.
3.12 ис.
3.13
ис.
3.13 ис.
3.14
ис.
3.14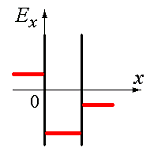 ис.
3.15
ис.
3.15