Полное термодинамическое равновесие. Основные законы теплового излучения. Локальное термодинамическое равновесие

Полное термодинамическое равновесие — это состояние, к ко­торому со временем должна прийти система, заключенная вну­три замкнутой полости. Такая полость представляет собой мо­дель абсолютно черного тела, поскольку любой луч, проникший внутрь сквозь бесконечно малое отверстие, будет полностью по­глощен в результате многократных отражений внутри полости, из какого бы материала ни состояли стенки или находящиеся внутри полости частицы. Соответственно установившееся при термодинамическом равновесии излучение называется равновес­ным тепловым излучением или излучением абсолютно черного тела. При полном термодинамическом равновесии температура и радиация внутри полости не меняются ни в пространстве, ни во времени, радиация не зависит от направления. Поэтому каж­дый элемент объёма или поверхности излучает столько же энер­гии, сколько подучает, и радиационный приток тепла отсутст­вует. Для равновесного теплового излучения выполняется ряд фундаментальных физических законов.

Закон Кирхгофа

При термодинамическом равновесии отношение коэффици­ента излучения вещества к его коэффициенту поглощения (функ­ция источника) не зависит от индивидуальных свойств вещества, а является универсальной функцией температуры и длины волны. Очевидно, что это отношение равно также интенсивности излучения абсолютно черного тела I_λ:

(6.1.10)

Иными словами, при термодинамическом равновесии функции источника для любых поглощающих веществ одинаковы и равны интенсивности излучения абсолютно черного тела. \Коэффици­енты излучения любых нечерных тел и т. д. оказываются меньше коэффициента излучения абсолютно черного тела.

Закон Планка

Интенсивность излучения абсолютно черного тела I_λ опреде­ляется функцией Планка:

Здесь h – постоянная Планка, с – скорость света (в вакууме), k – постоянная Больцмана, T – абсолютная температура.

Энергия излучения тем больше, чем выше температура, ее максимум приходится на некоторую длину волны. Солнце излучает при температуре 6000 К^O, и максимум излучения приходится на длину волны 0,475 мкм (видимый диапазон), поэтому его излучение называют коротковолновым. Максимум излучения Земли приходится на инфракрасный диапазон, поэтому ее излучение называют длинноволновым.

Закон Стефана—Больцмана

Выражение для интегральной интенсивности излучения абсо­лютно черного тела можно получить, проинтегрировав формулу (6.1.11) по всем длинам волн:

Здесь постоянная Стефана—Больцмана. Соответственно интегральный поток излучения' абсолютно черного тела (т. е. полное количество энергии, излучаемое в полусферу) равен

F_ч.т =πI=σT⁴ (6.1.15)

поскольку излучение абсолютно черного тела изотропно.

Локальное термодинамическое равновесие.

Все перечисленные законы справедливы при наличии полного термодинамического равновесия. Возникает вопрос, можно ли пользоваться ими для описания радиационных процессов в ат­мосфере.

Атмосфера безусловно не находится в состоянии термодина­мического равновесия. Она не является ни изотермической, ни замкнутой, в нее проникают излучения от внешних источников — от Солнца и земной поверхности. Эти излучения не могут нахо­диться в равновесии с собственным атмосферным излучением, поскольку температуры атмосферы и внешних источников сильно различаются.

Тем не менее в атмосфере обычно существует так называемое локальное термодинамическое равновесие, при котором в дан­ной точке различные видь энергии молекул распределяются так же, как и при полном термодинамическом равновесии. В таком случае, прежде всего, существует средняя кинетическая темпера­тура газа (см. п. 1.5), а также справедливы закон Кирхгофа и другие законы, связывающие характеристики излучения газа с его температурой. Однако очень важно отметить, что при ло­кальном термодинамическом равновесии лучистый приток тепла отличен от нуля. Атмосфера может как нагреваться, так и охла­ждаться в результате радиационного обмена. Перераспределе­ние энергии между молекулами осуществляется при столкнове­ниях, поэтому для установления локального термодинамического равновесия необходима достаточно большая частота столкнове­ний молекул, т. е. достаточная плотность воздуха (более подробно этот вопрос будет рассмотрен ниже). В земной атмосфере условия локального термодинамического равновесия выполня­ются вплоть до высот примерно 70 км.

Вывод уравнений переноса радиации (вопрос 11).

Так как спектральные области, в которых сосредоточена коротковолновая солнечная радиация и длинноволновая земная радиация практически не перекрываются, то перенос коротковолновой и длинноволновой радиации можно рассматривать отдельно. Рассмотрим перенос длинноволновой радиации. Для нее пренебрежимо мало рассеяние, поэтому им мы можем пренебречь. Кроме того будем считать, что выполняются условия локального термодинамического равновесия.

dz ϑ dl

Поглощение радиации зависит не от геометрической толщины слоя, а от количества поглощающего вещества, поэтому вместо высоты вводят новую переменную – поглощающую массу.

Это количество поглощающего вещества в столбе воздуха единичного сечения от земной поверхности до уровня Z. Согласно определению, поглощающая масса имеет размерность (обычно г/см²).

Примем степенную зависимость коэффициента поглощения от давления и температуры.

Удобно поправки на давление и температуру ввести не к коэффициентам поглощения, а к поглощающей массе, а именно ввести эффективную поглощающую массу.

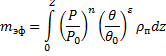
Запишем, еще не вводя эффективную поглощающую массу, выражение для изменения интенсивности восходящей длинноволновой радиации. Поглощение радиации в слое - , а излучение радии в слое - .

И, наконец, введя эффективную поглощающую массу, имеем:

По аналогии можно записать и для нисходящей радиации:

Сформулируем граничные условия. Будем считать, что Земля излучает, как серое тело. Тогда на уровне Земной поверхности ( ):

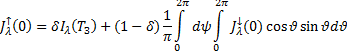
Здесь – температура подстилающей поверхности Земли, – коэффициент серости, – альбедо. Первый член в правой части описывает излучение земной поверхности, а второй – отраженную от земной поверхности нисходящую радиацию. На верхней границы атмосферы нисходящая длинноволновая радиация отсутствует, поскольку приходящая от Солнца длинноволновая радиация пренебрежимо мала. Таким образом, при и

При наличии облачности задача усложняется. Перенос радиации внутри облачного слоя представляет отдельный, весьма сложный вопрос. Однако в большинстве задач, имеющих значение для динамической метеорологии, облачность можно рассматривать как непрозрачную перегородку, излучающее как серое тело. В таком случае необходимо рассматривать перенос излучения в каждом безоблачном слое атмосферы, ограниченном облачными слоями.