10. Средняя хронологическая: ее значение, методика расчета.

10. Производные абсолютные показатели динамического ряда.

В зависимости от базы сравнения различают базисные и цепные показатели динамики. Базисные показатели динамики — это ре­зультат сравнения текущих уровней с одним фиксированным уров­нем, принятым за базу. Они характеризуют окончательный резуль­тат всех изменений в уровнях ряда за период от базисного до те­кущего уровня. Обычно за базу сравнения принимают начальный уровень динамического ряда. Цепные показатели динамики — это результат сравнения текущих уровней с непосредственно предше­ствующими. Они характеризуют интенсивность изменения уров­ней от срока к сроку.

Абсолютный прирост равен разности между текущим уровнем и уровнем более раннего периода. Интерпретацию абсолютного прироста осуществляют в тех же единицах измерения, в которых измеряют уровни ряда, с добавлением единицы времени, за кото­рую определено изменение. Например, абсолютный прирост объ­ема промышленной продукции составил 501 млрд руб. за квар­тал и 687 трлн руб. за год. Если текущий уровень уменьшился по сравнению с предыдущим периодом, то абсолютный прирост, имея отрицательное значение, характеризует абсолютную убыль (сокра­щение) уровня. Абсолютный прирост за единицу времени отражает абсолютную скорость изменения.

Цепный и базисные абсолютные приросты связаны между собой: сумма последовательных приростов равна соответсвующему базисному приросту за весь период.

19. Производные относительные показатели динамического ряда.

Для оценки эффективности изменения уровня динамического ряда используют относительные показатели динамики:

— коэффициент роста, выраженный в долях единицы;

— темп роста, выраженный в %. Коэффициент роста К_р определяют по формулам:

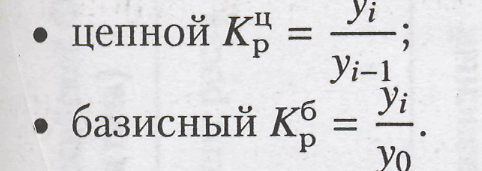
Взаимосвязь цепных и базисных коэффициентов роста заклю­чается в следующем:

а) произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период.

б) частное от деления последующего базисного коэффициента роста на предыдущий равна соответствующему цепному коэффи­циенту роста.

Для большей простоты и наглядности доказательства этой взаи­мосвязи используем данные за три периода:

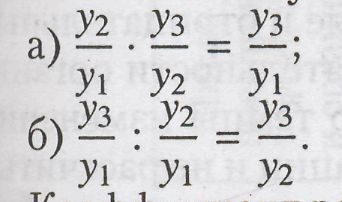
Коэффициент роста показывает, во сколько раз увеличился уро­вень динамического ряда по сравнению с базисным, а в случае уменьшения — какую часть базисного составляет сравниваемый уровень. Темпы и коэффициенты роста отличаются только едини­цами измерения. Формулы расчета темпов роста следующие:

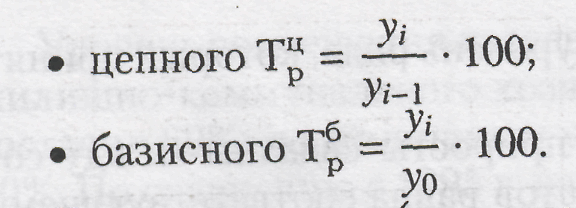
Темпы прироста (сокращения) так же, как и темпы роста, исчисляют по годам (цепным методом) и накопленным итогом за длительный период (базисным методом). Формулы расчета прироста следующие:

Темп прироста показывает, на сколько процентов изменилась величина уровня динамического ряда за изучаемый период време­ни.

20. Среднегодовые показатели роста и прироста (абсолютные и относительные).

Ребят, посмотрите по Елисеевой, не могу уже формулы сканировать! (стр 154)

20. Способы обработки динамических рядов.

Елисеева, стр 158

20. Интерполяция и экстраполяция в динамических рядах.

ЭКСТРАПОЛЯЦИЯ (от латин. extra - вне и второй части слова интерполяция, из polio - ровняю, выправляю). Вычисление по нескольким членам какого-нибудь статистического ряда таких его значений, которые находятся вне пределов данного ряда; противоп. интерполяция.

20. Значение индексов и их классификация.

Индексный метод является одним из важнейших методов в статистике. Индексы относятся к числу обобщающих показателей. Следует различать поня­тие индекса в широком и узком смысле.

В широком смысле индекс — это относительная величина, характеризующая изменения явлений во времени (динамику). Но подобные относительные величины могут быть рассчитаны лишь для простых явлений или однородных совокупностей, единицы которых могут быть суммированы. Такие совокупности называются соизмеримыми.

Индекс в узком смысле слова — это обобщающий показатель сравнения двух совокупностей, состоящий из элементов, непосредственно не поддающихся суммированию.

С помощью индексов решаются две основные задачи:

1) синтетическая задача — обобщение, синтез динамики отдельных элементов в сложные явления в одном обобщающем показателе (сводном индексе);

2) аналитическая задача — анализ влияния изменения отдельных факторов на изменение сложного явления.

Классификация индексов по различным признакам:

1) по степени охвата совокупности выделяют индивидуальные индексы (элементарные) и общие индексы (сводные или сложные);

2) по форме построения выделяют агрегатные, средневзвешенные (арифметические, гармонические) индексы;

3) по применяемым весам выделяют индивидуальные индексы с постоянными и переменными весами;

4) по состоянию явления выделяют индексы переменного состава, постоянного состава, структурных сдвигов;

5) по содержанию индексируемых величин выделя­ют индексы цен, физического объема товарообо­рота, себестоимости, трудоемкости и т.д.;

6) по базе сравнения выделяют динамические (базисные, цепные) индексы, индексы выполнения плана, планового задания, территориального сравнения.