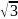4)Третий признак подобия треугольников.

Если три стороны одного треугольника пропорциональны трем сторонам другого, то эти треугольники подобны.

Дано: треугольники АВС и А₁В₁С_1, у которых АВ : А₁В₁ = АС : А₁С₁ = ВС : В₁С₁. Учитывая второй признак подобия треугольников, достаточно доказать, что угол А равен углу А₁.

рассмотрим треугольник АВС₂, у которого угол 1 (угол С₂АВ) равен углу А₁ и угол 2 (угол С₂ВА) равен углу В₁.Треугольники А₁В₁С₁ и АВС₂ подобны по первому признаку, следовательно, АВ : А₁В₁ = АС₂ : А₁С₁ = ВС₂ : В₁С₁. Сравнивая эти равенства с данными, получим: ВС = ВС₂, АС = АС₂; треугольники АВС и АВС₂ равны по трем сторонам, поэтому угол А равен углу 1 и угол 1 равен углу А₁, следовательно, А равен углу А₁, ч. т. д.

5)Средняя линия треугольника. Теорема о средней линии треугольника.

Средняя линия треугольника – отрезок, соединяющий середины его противоположных сторон.

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Доказательство через подобие треугольников.

6)Доказать свойство медиан треугольника.

1)Три медианы делят треугольник на 6 равновеликих. Доказательство проводится с помощью проведения высот.

2)Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины. Доказательство с помощью проведения средней линии (с. 147).

7)Докажите, что высота прямоугольного треугольника, опущенная из прямого угла делит его на два подобных треугольника, каждый из которых подобен исходному.

Дано: прямоугольный АВС, ВН – высота.

1.ВНС подобен АВС, т. к. угол АНВ = АВС, угол С – общий.

2.АВН подобен АВС, т. к. угол АВН = АВС, угол А – общий.

3.Угол С = 90 – угол А = 90 – НВС угол А равен углу НВС

Угол А = 90 – угол С = 90 – угол АВН угол С равен углу АВН

Из этого следует, что АНВ подобен ВНС, .

8)Пропорциональные отрезки в прямоугольном треугольнике.

1.Высота прямоугольного треугольника есть среднее геометрическое проекций катетов на гипотенузу.

2.Катет прямоугольного треугольника есть среднее геометрическое между гипотенузой и своей проекцией на гипотенузу.

9)Соотношения между сторонами и углами в прямоугольном треугольнике (синус, косинус, тангенс острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество. Значения синуса, косинуса и тангенса для углов 30°, 45°, 60°.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Основное тригонометрическое тождество: sin² A + cos² A = 1.

α	30	45	60
sin α
cos α
tg α		1

10)Докажите, что отрезок, соединяющий середины боковых сторон трапеции (средняя линия трапеции), параллелен основаниям и равен полусумме оснований.

Параллельность доказывается по теореме Фалеса, далее проводится диагональ и рассматриваются средние линии образующихся треугольников.

11)Свойство биссектрисы треугольника.

Биссектриса угла треугольника делит его противоположную сторону на отрезки, пропорциональные прилежащим сторонам. Доказательство проводится с помощью теоремы о треугольниках, имеющих равные углы и проведения общей высоты.

Окружность.

1. Взаимное расположение прямой и окружности. Свойство и признак касательной.

Прямая и окружность могут либо иметь две общие точки, либо иметь одну общую точку, либо не иметь общих точек.

Касательная – прямая, имеющая с окружностью одну общую точку, которая называется точкой касания.

Свойство касательной: касательная окружности перпендикулярна к ее радиусу, опущенному в точку касания. Следствие: отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, соединяющей эту точку с центром окружности.

Признак касательной: если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к нему, то она является касательной.

2. Вписанный угол. Теорема о вписанном угле. Следствия.

Вписанный угол – угол, вершина которого лежит на окружности, а обе стороны пересекают эту окружность.

Теорема: вписанный угол измеряется половиной дуги, на которую он опирается. Теорема имеет три случая: 1) сторона вписанного угла является диаметром; 2)диаметр является биссектрисой вписанного угла; 3) диаметр не является ни стороной, ни биссектрисой вписанного угла. Доказательство:

1.Дополнительное построение – центральный угол; далее доказательство проводится через внешний угол равнобедренного треугольника.

2.Доказательство по доказанному (извините за тавтологию).

3.Доказательство с помощью вычитания углов.

Следствия: вписанный угол, опирающийся на полуокружность – прямой; вписанные углы, опирающиеся на одну и ту же дугу, равны.

3. Теорема об отрезках пересекающихся хорд.

Если две секущие пересекаются в окружности, то угол между ними равен полусумме дуг, заключенных между ними. Доказательство: соединяем концы двух хорд, получаем 2 вписанных угла.

4. Свойство биссектрисы угла (теорема, следствие)

Теорема: любая точка биссектрисы неразвернутого угла равноудалена от его сторон. Обратно: если точка равноудалена от сторон угла, то она лежит на его биссектрисе. Доказывается с помощью построение прямоугольных треугольников.

Следствие: биссектрисы треугольника пересекаются в одной точке. Доказательство: проводим биссектрисы и высоты, далее по доказанной теореме.

5. Теорема о серединном перпендикуляре к отрезку.

Серединный перпендикуляр к отрезку – прямая, проходящая через отрезок под прямым углом и делящая его пополам.

Любая точка серединного перпендикуляра равноудалена от концов отрезка. Обратно: если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре.

Следствие: серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Доказательство: проводим серединные перпендикуляры к сторонам треугольника и отрезки, соединяющие точку их пересечения с вершинами, далее – по теореме.

6. Теорема о пересечении высот треугольника.

Высоты треугольника (или их продолжения) пересекаются в одной точке. Доказательство: через вершины треугольника проводятся вершины, параллельные основаниям, доказывается, что высоты маленького треугольника – серединные перпендикуляры к сторонам другого, и , следовательно, пересекаются в одной точке.

7. Четыре замечательных точки треугольника.

• Все биссектрисы треугольника пересекаются в одной точке. Доказательство с использованием свойства биссектрисы угла.

• Все серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Доказательство с использованием свойства серединного перпендикуляра.

• Все высоты треугольника (или их продолжения) пересекаются в одной точке. Доказательство через построение большего треугольника и свойство серединного перпендикуляра.

• Все медианы треугольника пересекаются в одной точке и этой точкой делятся в отношении 2:1, считая от вершины. Доказательство через среднюю линию и подобие треугольников.