
- •Лекция №8 Магнитное поле в вакууме
- •Вопрос №1. Источники магнитного поля. Взаимодействие токов. Магнитные силы
- •Вопрос 2. Магнитостатическое поле и его свойства Индукция магнитного поля
- •Сила Ампера
- •Магнитный момент
- •Вращающийся момент. Принцип суперпозиции магнитных полей
- •Вопрос №3. Закон Био – Савара – Лапласа
- •Вопрос №4. Напряженность магнитного поля
- •Вопрос №5. Магнитное поле прямолинейного проводника с током
- •Вопрос №6.Магнитное поле кругового проводника с током. Магнитные поля соленоида и тороида
- •Вопрос №7. Взаимодействие параллельных токов. Единица силы тока - Ампер
- •Вопрос №8. Действие электрического и магнитного полей на движущиеся заряды
- •Вопрос №9. Эффект Холла
- •Вопрос №10. Закон полного тока и его применение. Теорема Гаусса
- •Закон постоянного тока для вектора напряженности
Магнитный момент
М
1.3
![]()
В СИ {A∙м2}.Направление магнитного момента находится по правилу «буравчика».
Вращающийся момент. Принцип суперпозиции магнитных полей
И
1.4
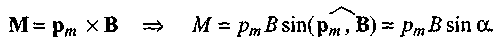
Е
1.5
![]()
Из формулы (1.5) следует, что В = Mmax/(I ∙S), т.е. индукция магнитного поля в данной точке поля численно равна отношению максимального вращающего момента Мmax, который действуют на маленькую плоскую рамку, помещенную в область поля в окрестности этой точки, к площади рамки и силе тока в ней. Отметим, что оба эти определения для В согласуются друг с другом.
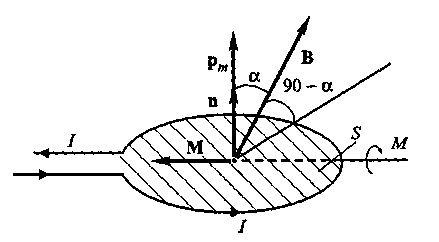
Рис.4
Отметим, что индукцию В магнитного поля системы проводников с токами определяют, используя принцип суперпозиции, т.е.
1.6
где В, — индукция поля, создаваемого в данной точке пространства отдельным проводником с номером i (i = 1, 2, ...,n).
Вопрос №3. Закон Био – Савара – Лапласа
Магнитные поля, создаваемые постоянными токами различной конфигурации, изучали на опыте французские физики Ж. Био и Ф. Савар (1791-1841). Накопленный экспериментальный материал позволил П. Лапласу получить формулу для расчета магнитных полей по известному расположению элементов тока I dI в пространстве. Согласно закону Био — Савара — Лапласа каждый элемент dI тонкого проводника с током I создает магнитное поле (рис.5), индукция dВ которого в точке А с радиус-вектором r относительно элемента dI определяется по формуле
1.7
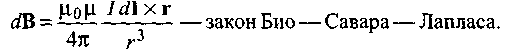
Здесь μ0 — магнитная постоянная, числовое значение которой в Международной системе (СИ) равно 4π ∙ 10-7 Гн/м (Гн — генри — единица индуктивности, μ магнитная проницаемость среды.
Рис.5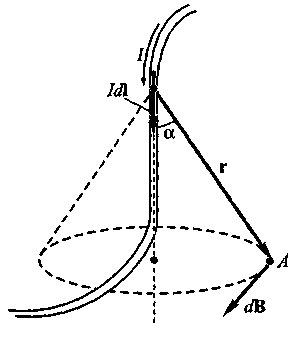
Направление вектора dВ определяется по правилам буравчика или векторного произведения dI x r, например, по правилу правой руки.
Вопрос №4. Напряженность магнитного поля
Вместе с вектором индукции В, который характеризует силовое действие магнитного поля на движущиеся заряды, часто вводится вспомогательный вектор Н, называемый напряженностью магнитного поля.
Напряженность определяется как отношение индукции поля в вакууме к магнитной постоянной μ0:
1.8![]()
По аналогии с учетом об электрическом поле, где силовой вектор Е называется напряженностью, а вспомогательный вектор Д – смещением, следовало бы и в учении о магнетизме назвать силовой вектор В напряженностью магнитного поля, а вспомогательный Н – магнитной индукцией. Путаница в терминологии возникла еще тогда, когда смысл векторов В и Н был недостаточно ясен.
Вопрос №5. Магнитное поле прямолинейного проводника с током
Как уже отмечалось, закон Био — Савара — Лапласа вместе с принципом суперпозиции позволяет рассчитать магнитные поля, создаваемые проводниками с током любых конфигураций в изотропной среде с магнитной проницаемостью μ.
В качестве примера рассмотрим магнитное поле прямого проводника с током. Пусть имеется участок проводника конечной длины l (рис. 6) между точками 1 и 2. Определим напряженность Н магнитного поля в точке А на расстоянии х от проводника длиной l , разделив его на элементы длиной dl.
Рис.6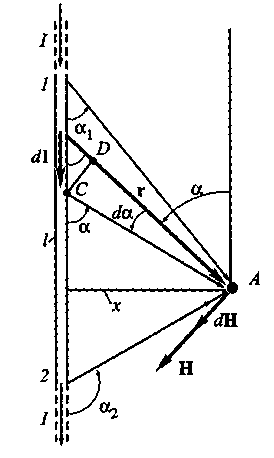
С
1.х1
![]()
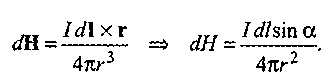
Поэтому для определения модуля результирующей напряженности в соответствии с принципом суперпозиции проинтегрируем последнее выражение и получим:
1.9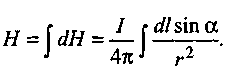
Из рис. 6 следует:
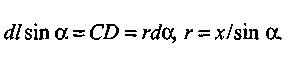
П
1.10
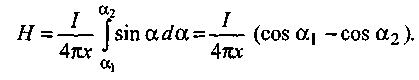
Согласно формуле (1.х1), модуль вектора индукции в результате имеет вид:
1.11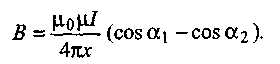
Заметим, что направления векторов Н и В результирующего поля прямого тока можно определять по правилу буравчика.
Если длина l проводника с током намного больше расстояния х, то α→0, α2→π, и для такого бесконечно длинного проводника получим
1.12![]()
