
- •Лекция № 6 Электрическое поле в веществе
- •Вопрос №1. Проводники. Явление электростатической индукции
- •Вопрос №2. Распределение избыточного заряда в заряженном проводнике. Экраны заземления
- •Вопрос №3. Электроемкость уединенного проводника. Конденсаторы и их электроемкость. Соединения конденсаторов
- •Вопрос №4. Энергия заряженных тел
- •Вопрос №5. Энергия электростатического поля. Объемная плотность энергии
Вопрос №4. Энергия заряженных тел
П
1.10
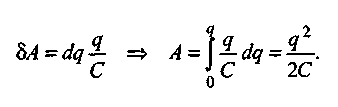
1.11
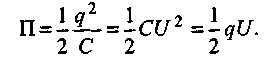
1.12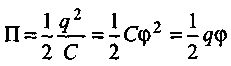
Здесь С иφ — соответственно электроемкость и потенциал проводника; q—его заряд.
В общем случае заряды могут быть распределены по объему диэлектрика
(ρ =dq / dV) либо по поверхности заряженного проводника или наэлектризованного диэлектрика (σ = dq / dS). Энергию такой системы зарядов можно определить путем интегрирования выражения dП = 1/2φ·dq по поверхности S (dq = σ·dS) и объему V(dq = ρdV):
1.13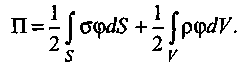
Вопрос №5. Энергия электростатического поля. Объемная плотность энергии
Энергию П, определяемую по формулам (1.11)—(1.13), можно интерпретировать как энергию W электростатического поля этой системы зарядов (W= П). Покажем это на примере плоского конденсатора. Электроемкость такого конденсатора С = εε0·S / d,a разность потенциалов между обкладками U=Ed (Е—напряженность поля). Подставив выражения для С и U в формулу (1.11), получим
1.14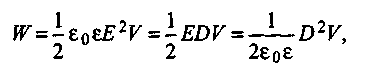
где V=Sd — объем конденсатора; D = εε0· E — электрическое смещение.
В формуле (1.14) энергия выражена через величины Е и D, характеризующие электростатическое поле конденсатора, и объем V, в котором сконцентрировано это поле. Следовательно, W— энергия электростатического поля в объеме V.
Поскольку поле внутри плоского конденсатора однородно (Е(х,у, z) = const), его энергия W равномерно распределена по объему V. Тогда объемная плотность энергии равна:
1.15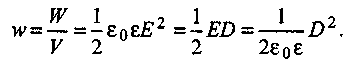
Ф
1.16
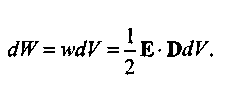
Полную энергию электрического поля в объеме V определяем интегрированием:
1.17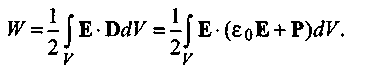
Если
существует система из N неподвижных
точечных зарядов, то она обладает
потенциальной энергией, равной половине
суммы взаимных потенциальных энергий
Пik
всевозможных
пар точечных зарядов qi
и qk
(i = 1, 2, ..., N, к = 1, 2, ..., N), находящихся
на расстоянии rik
друг от друга (см. формулу
![]() ).
Суммируя по всем значениям i
и j
без учета энергии самовоздействия этих
зарядов (самих на себя, т.е.i
≠ k
), получим:
).
Суммируя по всем значениям i
и j
без учета энергии самовоздействия этих
зарядов (самих на себя, т.е.i
≠ k
), получим:
1.18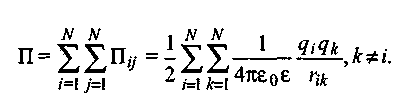
Можно доказать, что эта энергия не имеет минимума при конечных значениях rik , следовательно, изолированная система неподвижных электрических зарядов не может находиться в состоянии устойчивого равновесия (теорема Ирншоу). В связи с этим устойчивые системы зарядов (атомы, молекулы, ионы) всегда являются динамическими системами.
Задача 3. 125 маленьких шаровой формы капелек воды, заряженных до потенциала φ относительно Земли, соединились в одну большую каплю (шаровой фрмы). Каким окажется потенциал φ1 такой большой капли по сравнению с потенциалом φ ?
Решение:
Из
![]() следует, что
следует, что![]() , где С1
– электроемкость большой капли, q1
– ее заряд, q
– заряд маленькой капли. q1=125q
, где С1
– электроемкость большой капли, q1
– ее заряд, q
– заряд маленькой капли. q1=125q
Объем
большой капли радиусом R
равен 125 об’емам маленьких капель,
радиус которых r,
т.е.
![]() ,
откуда
,
откуда
![]() ,
значит R
= 5r.
,
значит R
= 5r.
Электроёмкость шара пропорциональна его радиусу. Следовательно : С1 = 5С, где С – электроемкость малой капли.
Потенциал маленькой капли : φ = q/C.
Потенциал большой капли равен:
![]() ,
т.е. он увеличен по сравнению с потенциалом
малой капли в 25 раз.
,
т.е. он увеличен по сравнению с потенциалом
малой капли в 25 раз.
Задача 4. Две разноименно наэлектризованные пластины площадью 100 см2 каждая притягивается друг к другу с илой равной 0,04 Н. Определить напряженность поля между пластинами, если они разделены слоем спирта. Диэлектрическая проницаемость для спирта равна 26.
Решение:
сила взаимодействия пластин конденсатора![]() ,
а напряженность
,
а напряженность![]() .
Возведем Е в квадрат и поделим на F.
.
Возведем Е в квадрат и поделим на F.
![]() ,
откуда
,
откуда
![]() .
Подставив значения в конечную формулу
получим: Е = 18,6·104
(В/м).
.
Подставив значения в конечную формулу
получим: Е = 18,6·104
(В/м).
Задача 5. Шар радиусом 25 см заряжен до потенциала 600 В и соединен проводником с землей. Сколько теплоты выделитсяв проводнике ?
Решение: при уходе заряда шара в землю совершается работа:
![]() ,
где С = 4πε · ε0
·
r
= 4· 3,14 · 8,85 · 10-12
· 0,25 ≈ 2,8 · 10-11
(Ф).
,
где С = 4πε · ε0
·
r
= 4· 3,14 · 8,85 · 10-12
· 0,25 ≈ 2,8 · 10-11
(Ф).
Но при этом А = Q, то высчитав по формуле, приведенной выше значение работы, определим количество теплоты.
![]() (Дж). А
= Q
=5 · 10-6
(Дж) или Q
= 0,24 · 5 · 10-6
=
(Дж). А
= Q
=5 · 10-6
(Дж) или Q
= 0,24 · 5 · 10-6
=
=1,2· 10-6 калл.(внесистемные единицы).
Литература:
И.И. Наркевич, Э.И. Волмянский, С.И.Лобко. Физика. – Мн.: 0.0.0. «Новое знание», 2004.
А.Н. Ремизов. Курс физики, Электроники и кибернетики. – М.: Высшая ШК., 1982.
П.С. Кудрявцев. Курс истории физики. – М.: Просвещение, 1974.
